GCSE Tutoring Programme
"Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring."
In order to access this I need to be confident with:
Factors and multiples Constructing Venn diagramsThis topic is relevant for:

HCF And LCM
Here we will learn about HCF and LCM (the highest common factor and the lowest common multiple), including how to calculate the HCF and LCM of two or more numbers and recognise when to calculate the HCF or the LCM from worded problems.
There are also HCF and LCM worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is HCF and LCM?
The HCF and LCM are two abbreviations for the highest common factor (HCF) and the lowest common multiple (LCM).
- The HCF is the largest integer (whole number) that two or more numbers can be divided by. Other names for this include the greatest common divisor (GCD) and the greatest common factor (GCF).
For example, find the HCF of 8 and 12.
Let’s start by writing the factors of 8 and 12.
Factors of {\bf{8}} : \ 1, \ 2, \ 4, \ 8
Factors of {\bf{12}} : \ 1, \ 2, \ 3, \ 4, \ 6, \ 12
There are several numbers that occur in both lists (1, \ 2, and 4).
The highest positive integer that occurs in each list is 4, and so the highest common factor of 8 and 12 is 4. - The LCM is the smallest integer that is a multiple of two or more composite numbers (exists within the multiplication table of each number). Another name for this is the least common multiple.
For example, find the LCM of 8 and 12.
Let’s start by writing the first 12 multiples of 8 and 12.
Multiples of {\bf{8}} : \ 8, \ 16, \ 24, \ 32, \ 40, \ 48, \ 56, \ 64, \ 72, \ 80, \ 88, \ 96
Multiples of {\bf{12}} : \ 12, \ 24, \ 36, \ 48, \ 60, \ 72, \ 84, \ 96, \ 108, \ 120, \ 132, \ 144
There are several values that occur in both lists (24, \ 48, \ 72, and 96). The lowest of these is 24, hence the lowest common multiple of 8 and 12 is \bf{24} .
What is HCF and LCM?

Prime factor decomposition
To calculate the HCF or LCM of two or more numbers, we can write out a list of factors or multiples as we have above, however this approach can be very time consuming and can be complicated when dealing with factors and multiples of large numbers ( 3 digit numbers in particular).
We can therefore utilise prime factors to calculate these values.
The fundamental theorem of arithmetic states that every positive integer is either a prime number, or can be written as a product of its prime factors. Every number has a unique set of prime factors.
By presenting prime factors within a Venn diagram, we can quickly determine both the HCF and LCM of the two or more numbers in the question.
For example,
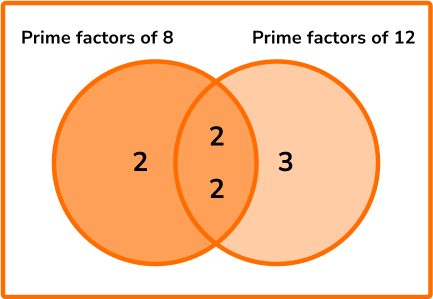
8=2\times{2}\times{2}
12=2\times{2}\times{3}
The intersection of the two circles contains the highest common factor where we multiply the values within the intersection together.
Here, the HCF of 8 and 12 is equal to 2\times{2}=4.
The union of the two circles contains the lowest common multiple where we multiply the values within both circles together.
Here, the LCM of 8 and 12 is equal to 2\times(2\times{2})\times{3}=24.
Notice that the values for the HCF and LCM match those values previously mentioned using the alternative method.
Furthermore, as the lowest common multiple is calculated by multiplying all of the factors together within the Venn diagram, the lowest common multiple can be found by multiplying the highest common factor by the remaining prime factors.
\text{LCM } = \text{ HCF } \times \text{ remaining prime factors}This allows us to solve problems where we are given the HCF and LCM of two numbers and we need to determine the original two numbers.
How to calculate the highest common factor
In order to calculate the highest common factor of two or more numbers:
- State the product of prime factors for each number, not in index form.
- Write all the prime factors for each number into a Venn diagram.
- Multiply the prime factors in the intersection to find the HCF.
Explain how to calculate the highest common factor

How to calculate the lowest common multiple
In order to calculate the lowest common multiple of two or more numbers:
- State the product of prime factors for each number, not in index form.
- Write all the prime factors for each number into a Venn diagram.
- Multiply each prime factor in the Venn diagram to find the LCM.
Explain how to calculate the lowest common multiple


HCF and LCM worksheet

Get your free hcf and lcm worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
HCF and LCM worksheet

Get your free hcf and lcm worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on factors, multiples and primes
HCF and LCM is part of our series of lessons to support revision on factors, multiples and primes. You may find it helpful to start with the main factors, multiples and primes lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
HCF and LCM examples
Example 1: HCF of two simple composite numbers
Calculate the highest common factor of 30 and 42.
- State the product of prime factors for each number, not in index form.
2Write all the prime factors for each number into a Venn diagram.
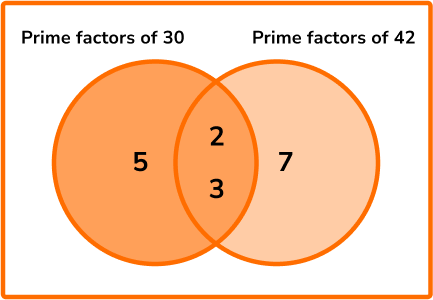
3Multiply the prime factors in the intersection to find the HCF.
HCF =2\times{3}=6.
Example 2: LCM of two simple composite numbers
Calculate the lowest common multiple of 16 and 18.
State the product of prime factors for each number, not in index form.
18=2\times{3}\times{3}
Write all the prime factors for each number into a Venn diagram.
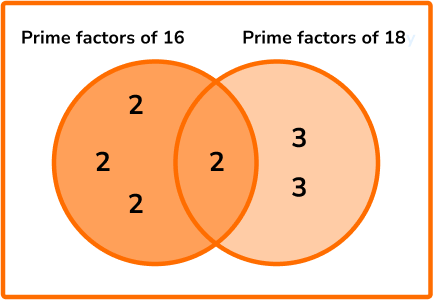
Multiply each prime factor in the Venn diagram to find the LCM.
LCM =(2\times{2}\times{2})\times{2}\times(3\times{3})=8\times{2}\times{9}=144.
Example 3: HCF worded problem
120 \ ml of red paint and 156 \ ml of blue paint are mixed together to create a tin of purple paint. The paint is then distributed equally into sample tubes. Each tube must contain the same amount of paint that must be over 20 \ ml.
What is the maximum number of tubes that can be filled with the minimum amount of paint?
State the product of prime factors for each number, not in index form.
156=2\times{2}\times{3}\times{13}
Write all the prime factors for each number into a Venn diagram.
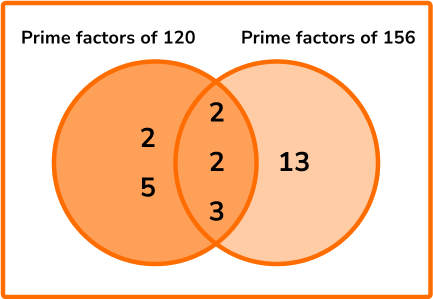
Multiply the prime factors in the intersection to find the HCF.
HCF =2\times{2}\times{3}=12.
The total amount of paint is 120 + 156 = 276 \ ml.
Dividing 276 \ ml into 12 equal shares (the HCF), we have
276\div{12}=23.
As each tube must contain over 20 \ ml of paint, we must have 12 tubes, each containing 23 \ ml of paint.
Example 4: LCM worded problem
A plumber is fixing multiple leaking pipes. Pipe A drips water every 12 seconds. Pipe B drips water every 22 seconds. Both pipes drip at the same time.
How much time passes before they next drip at the same time? Write your answer using minutes and seconds.
State the product of prime factors for each number, not in index form.
22=2\times{11}
Write all the prime factors for each number into a Venn diagram.
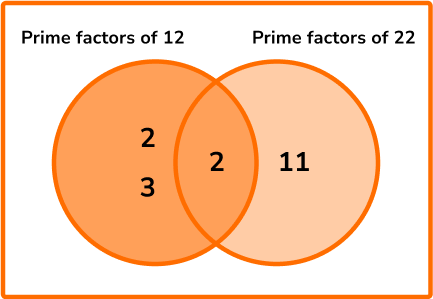
Multiply each prime factor in the Venn diagram to find the LCM.
LCM =(2\times{3})\times{2}\times{11}=6\times{2}\times{11}=132
132 seconds pass. Converting this to minutes and seconds is 2 minutes and 12 seconds (60 + 60 + 12 = 132, with 60 seconds = 1 minute).
How to calculate the original values given the HCF and the LCM
In order to calculate the original values given the HCF and the LCM:
- Divide the LCM by the HCF.
- Calculate the product of primes of the remainder.
- Determine which prime factors match each original number.
Explain how to calculate the original values given the HCF and the LCM

Example 5: calculate the numbers, given the HCF
The highest common factor of 3 numbers is 7. The product of their remaining prime factors is 30 and each number is greater than 10. Determine the value of the three numbers.
Divide the LCM by the HCF to determine the remainder.
As we already know the remainder (30), we can move on to step 2.
Calculate the product of primes of the remainder.
Using a prime factor tree, the product of primes for 30 is
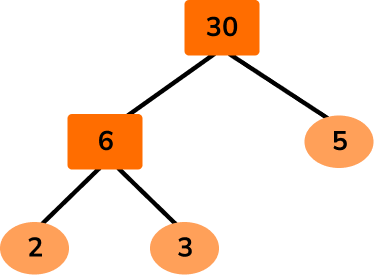
30=2\times{3}\times{5}
Determine which prime factors match each original number.
As each value is greater than 10, the HCF 7 must be a factor of all 3 numbers and it must be multiplied by another factor. 30 has 3 prime factors, 2, \ 3, and 5 and so the original three numbers are:
A=7\times{2}=14
B=7\times{3}=21
C=7\times{5}=35
Example 6: calculate the original numbers given the HCF and LCM
Two numbers A and B have the following number properties
- HCF (A,B) = 7
- LCM (A,B) = 2310
- A is divisible by 3
- B is an even number
- 100<A<B
Determine the values of A and B.
Divide the LCM by the HCF to determine the remainder.
Calculate the product of primes of the remainder.
Using a prime factor tree, the product of primes for 330 is
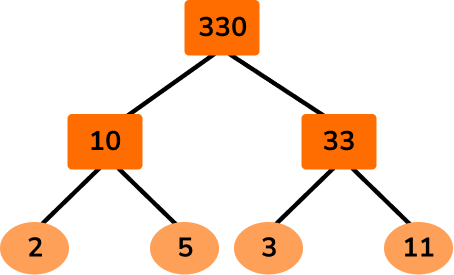
330=2\times{3}\times{5}\times{11}
Determine which prime factors match each original number.
As A is divisible by 3, two factors of A must be 3 and 7 (the HCF).
As B is even, two factors of B must be 2 and 7 (the HCF).
Writing this up so far, we have
A=3\times{7}\times{x}
B=2\times{7}\times{y}
As 330=2\times{3}\times{5}\times{11}, we have the remaining factors of 5 and 11 to place.
As 100<A<B, both A and B are greater than 100 with A being smaller than B. The only way this is possible is by making x=5 and y=11.
This means that
A=3\times{7}\times{5}=105
B=2\times{7}\times{11}=154
The solution is A = 105 and B = 154.
Common misconceptions
- Calculating the HCF instead of the LCM (and vice versa)
A very common misconception is mixing up the highest common factor with the lowest common multiple. Factors are composite numbers that are split into smaller factors. Multiples are composite numbers that are multiplied to make larger multiples.
- Incorrect evaluation of powers
It is possible to write prime factors into a Venn diagram with their associated exponent or power. This only becomes an issue when the powers are not correctly interpreted.
Take for example the numbers 12 and 18.
12=2^{2}\times{3}
18=2\times{3}^{2}
Here, 2^{2}=2\times{2}=4 is correct, however the same misconception could then be continued to 3^{2}=3\times{2}=6, which is incorrect. Instead, 3^{2}=3\times{3}=9.
This will have an impact on the value of the HCF and the LCM.
Practice HCF and LCM questions
1. Calculate the HCF of 54 and 60.




60=2\times{2}\times{3}\times{5}
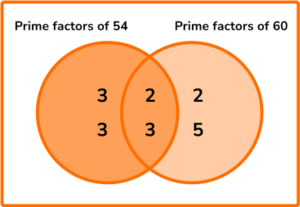
HCF (54,60) = 2\times{3}=6
2. Calculate the LCM of 24 and 32.




32=2\times{2}\times{2}\times{2}\times{2}
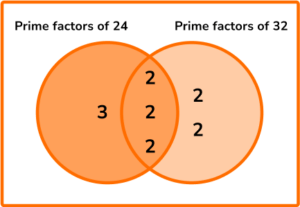
LCM (24,32) = 3\times(2\times{2}\times{2})\times(2\times{2})=3\times{8}\times{4}=96
3. Two off cut lengths of ribbon measure 1.2 \ m and 80 \ cm. Each piece of ribbon needs to be cut into the fewest number of pieces the same length. What is the length of each piece?




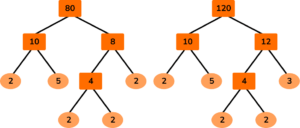
80=2\times{2}\times{2}\times{2}\times{5}
120=2\times{2}\times{2}\times{3}\times{5}
HCF (80,120) = 2\times{2}\times{2}\times{5}=40
4. Two runners leave the start line of a 200 \ m track on the whistle. It takes runner A \ 1 minute to run 1 lap of the track and runner B \ 1 minute and 12 seconds. What distance will runner B have travelled when they next cross the start line at the same time?




Converting both lap times to seconds, runner A takes 60 seconds, and runner B takes 72 seconds.
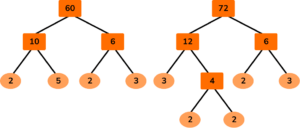
60=2\times{2}\times{3}\times{5}
72=2\times{2}\times{2}\times{3}\times{3}
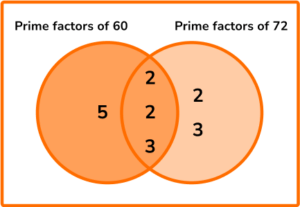
HCF (60,72) = 2\times{2}\times{3}=12
LCM (60,72) = 5\times{12}\times(2 \times 3)=5 \times 12 \times 6 = 360
360 seconds = 6 minutes
6\div{1.2}=5 laps
5\times{200}=1000 \ m=1 \ km
5. The highest common factor of two numbers is 35. The product of the remaining factors is 33. Both original numbers contain three digits. What is the difference between the two original numbers?




Smaller number: 35\times{3}=105
Larger number: 35\times{11}=385
385-105 = 280
6. Two numbers x and y have the following number properties,
- \text{LCM}(x,y)=96
- \text{HCF}(x,y)=8
- 2<x<y<40
What is the value of x+y?




12=2\times{2}\times{3}
8\times{2}\times{2}=32
8\times{3}=24
32+24=56
HCF and LCM GCSE questions
1. A stables needs to divide their two fields into equal sized paddocks for some horses.
Field 1 is 240 \ m^{2}. Field 2 is 160 \ m^{2}. Each horse must have at least 42 \ m^{2}.
a) What is the minimum possible area for each paddock?
b) What is the maximum number of horses that can use these two fields?
(4 marks)
(a)
240=2^4 \times 3 \times 5 \ or \ 240=2 \times 2 \times 2 \times 2 \times 3 \times 5
(1)
160=2^5 \times 5 \ or \ 160=2 \times 2 \times 2 \times 2 \times 2 \times 5
(1)
HCF(240,160)=80 \ m^2(1)
(b)
2+3=5 \ or \ (240+160) \div 80=5
(1)
2. Given that 6480=2^{4} \times 3^{4} \times5, simplify the ratio 10800 :6480.
(4 marks)
(1)
HCF(10800,6480)=2^{4} \times 3^{3} \times 5(1)
Remaining factors are 5 (for 10800 ) and 3 (for 6480).
(1)
5:3(1)
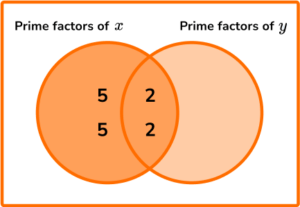
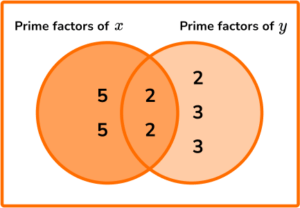
3. The lowest common multiple of x and y is 2^{3} \times 3^{2} \times 5^{2} where x is a square number such that 36<x<225.
a) Calculate the exact value of x.
b) The highest common factor of x and y is 4.
Determine the value of y. Use the Venn diagram below to help you.

(5 marks)
(a)
x=2^2 \times 5^2 \ or \ x=(2 \times 5)^2
(1)
x=100(1)
(b)
(1)
(1)
y=(2 \times 2) \times (2 \times 3 \times 3)=4 \times 18=72(1)
Learning checklist
You have now learned how to:
-
Use the concepts and vocabulary of prime numbers, factors (or divisors), multiples, common factors, common multiples, highest common factor, lowest common multiple, prime factorisation, including using product notation and the unique factorisation property of any given number.
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.