One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
Arithmetic Factors Multiples Venn diagram Two way tablesThis topic is relevant for:

Prime Numbers
Here we will learn about prime numbers, including what they are, how we can determine whether a number is prime, and how to solve problems that involve prime numbers.
There are also prime number worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What are prime numbers?
Prime numbers are positive integers (whole numbers) that have only two factors, themselves and 1.
This means that you cannot divide a prime number by any number apart from 1 or itself, and get an integer answer.
A number that is not prime is called a composite number.
There are 25 prime numbers between 1 and 100. These are:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97.
Notice that,
1 is not a prime number as it has only 1 factor.
2 is the only even prime number.
You should be able to recall the first 8 prime numbers (up to 20 ) and be able to determine whether a number is prime by looking at the factors of the number.
To determine whether the number is prime, check whether it has any factors other than itself and 1, either manually or by using a number trick. If the number has a factor that is not itself or 1, it is not prime.
There are a few useful number tricks that can help us determine whether a number is divisible by an integer and therefore has that integer as a factor:

Once we have considered these number tricks, we need to look for divisibility by other numbers. We don’t, however, need to consider every number.
The reason for this is that for a number to be divisible by 4 or 6 or any multiple of 2, it must also be divisible by 2, which is something we have already checked.
For a number to be divisible by 6 or 9 or any multiple of 3, it must also be divisible by 3, which is something that we have already checked.
This pattern continues and means that we only need to check for divisibility by other prime numbers, starting with the number 7.
What are prime numbers?

How to find prime numbers
In order to determine whether a number is a prime number:
- Use the number tricks to see whether \bf{2, 3} or \bf{5} is a factor.
- If they are not factors, test for divisibility by other prime numbers, starting with \bf{7}.
- State your conclusion with a reason.
Explain how to find prime numbers

Prime numbers worksheet

Get your free prime numbers worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Prime numbers worksheet

Get your free prime numbers worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on factors, multiples and primes
Prime numbers is part of our series of lessons to support revision on factors, multiples and primes. You may find it helpful to start with the main factors, multiples and primes lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Prime numbers examples
Example 1: two digit number
Is 53 a prime number?
- Use the number tricks to see whether \bf{2, 3} or \bf{5} is a factor.
The last digit is not a 2, 4, 6, 8, or 0 so it is not a multiple of 2.
Adding the digits together we have 5+3=8 and so it is not a multiple of 3.
The last digit is not a 5 or a 0 and so it is not a multiple of 5.
2If they are not factors, test for divisibility by other prime numbers, starting with \bf{7}.
We need to continue dividing 53 by successive prime numbers until we reach the first prime number that is greater than \sqrt{53}.
\sqrt{53} \approx 7.3 so we only need to try prime numbers less than this.
Start by dividing by 7:
As 53\div{7}=7.57142857 \ 7 is not a factor of 53.
The next prime number is 11, which is greater than 7.3 so there are no more integers that we need to try.
3State your conclusion with a reason.
53 is a prime number as it only has two factors, 1 and 53.
Example 2: three digit number
Is 223 a prime number?
Use the number tricks to see whether \bf{2, 3} or \bf{5} is a factor.
The last digit is not a 2, 4, 6, 8, or 0 so it is not a multiple of 2.
Adding the digits together we have 2+2+3=7 and so it is not a multiple of 3.
The last digit is not a 5 or a 0 and so it is not a multiple of 5.
If they are not factors, test for divisibility by other prime numbers, starting with \bf{7}.
As 223 is not divisible by 2, 3, or 5, we need to divide 223 by prime numbers until we reach the prime number that is greater than \sqrt{223}.
223 \approx 14.9
The prime numbers up to 14.9 (excluding 2, 3, and 5 ) are: 7, 11 and 13.
Completing these calculations, and rounding when necessary, we have:
\begin{aligned} 223\div{7}&=31.9 \text{ (1dp)}\\\\ 223\div{11}&=20.3 \text{ (1dp)}\\\\ 223\div{13}&=17.2 \text{ (1dp)} \end{aligned}
There are no other numbers that we can divide 223 by and get an integer answer except for 1 and 223.
State your conclusion with a reason.
223 is a prime number as it has only two factors, 1 and 223.
Example 3: four digit number
Is 2073 a prime number?
Use the number tricks to see whether \bf{2, 3} or \bf{5} is a factor.
The last digit is not a 2, 4, 6, 8, or 0 so it is not a multiple of 2.
Adding the digits together we have 2+0+7+3=12 which is a multiple of 3.
Dividing 2073 by 3 we have:
2073\div{3}=691
If they are not factors, test for divisibility by other prime numbers, starting with \bf{7}.
As we know that 2073 is divisible by 3, we do not need to carry out any further divisions.
State your conclusion with a reason.
2073 is not a prime number because 3\times{691}=2073.
Example 4: determine the prime number from a list of numbers
One of the following numbers is prime. Identify the prime number.

Use the number tricks to see whether \bf{2, 3} or \bf{5} is a factor.
The last digit of 14 is a 4 and so 14 is a multiple of 2.
The last digit of 25 is a 5 and so 25 is a multiple of 5.
9 is a multiple of 3.
The final two numbers are 61 and 259. As 61 is a smaller number, it is easiest to determine whether 61 is prime.
61 does not end in a 2, 4, 6, 8, or 0 and so 61 is not a multiple of 2.
6+1=7 and so 61 is not a multiple of 3.
61 does not end in a 5 or 0 and so it is not a multiple of 5.
If they are not factors, test for divisibility by other prime numbers, starting with \bf{7}.
We need to see whether 61 is divisible by any other prime number up to \sqrt{61} which is approximately 7.8. Therefore we only need to check to see whether 61 is divisible by 7.
61\div{7}=8.71\text{ (2dp)}
61 is not divisible by 7 and is therefore prime.
State your conclusion with a reason.
61 is the prime number as it only has 2 factors, 1 and 61.
Note: 259=7\times{37}
Problem solving with prime numbers
In order to place numbers into a diagram / table:
- Determine what each box / section of the diagram represents.
- Place each number one-by-one into the diagram.
- Determine the frequency of values in each box / section if required.
Problem solving with prime numbers

Problem solving with prime numbers examples
Example 5: complete the diagram (two way table)
Place the set of numbers N=\{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\} into the two-way table below.
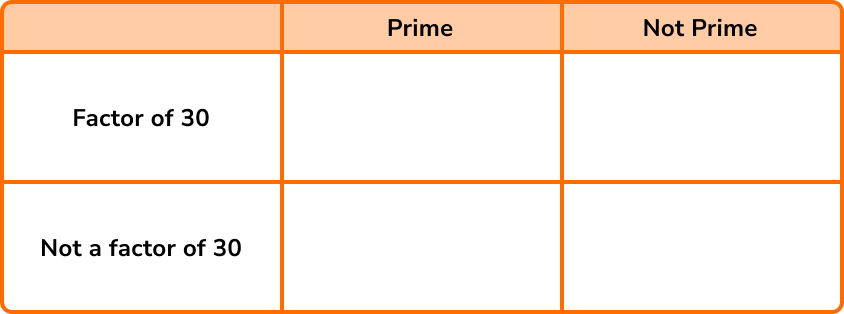
Determine what each box / section of the diagram represents.
Make a mental note of what each box represents:

Place each number one-by-one into the diagram.
The factors of 30 are: 1, 2, 3, 5, 6, 10, 15, and 30.
Given that the values we need to place in the two way table are 1-10, we do not need to include 15 and 30 in the table.
1 is not a prime number but it is a factor of 30.
2 is a prime number and it is a factor of 30.
3 is a prime number and it is a factor of 30…
and so on until we get:
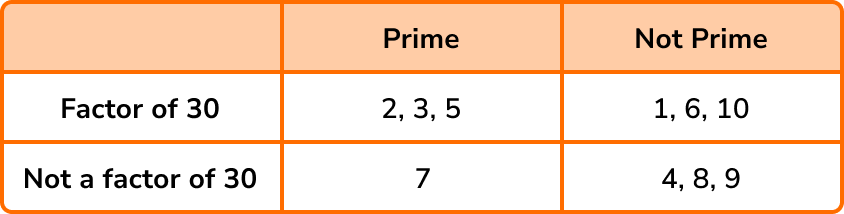
Determine the frequency of values in each box / section if required.
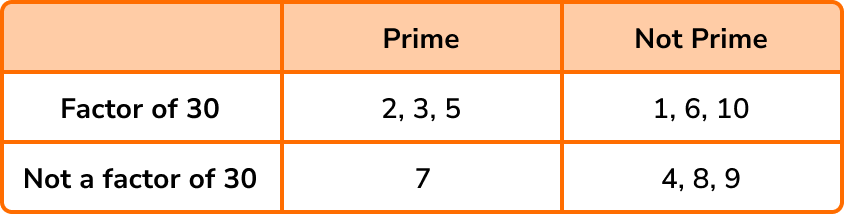
This question does not require us to show the frequency of values in each box and so the final solution is:
Example 6: complete the diagram (Venn diagram)
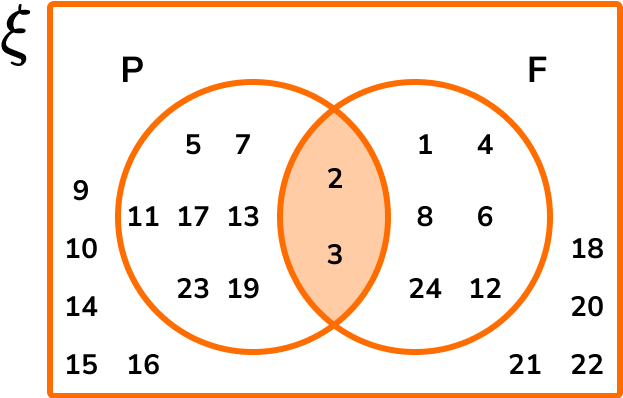
The Venn diagram below represents the two sets P=\{ Prime \} and F=\{ Factor of 24 \}.
Given that ξ=\{x is an integer such that 0 < x \leq 24 \}, complete the Venn diagram.
Use your Venn diagram to write down the frequency of values in the sets.
i) P
ii) P \cap F
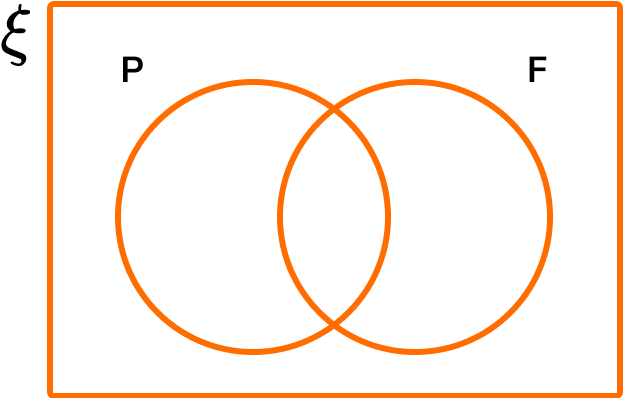
Determine what each box / section of the diagram represents.
Making a mental note of what each section of the venn diagram represents, we have:
Place each number one-by-one into the diagram.
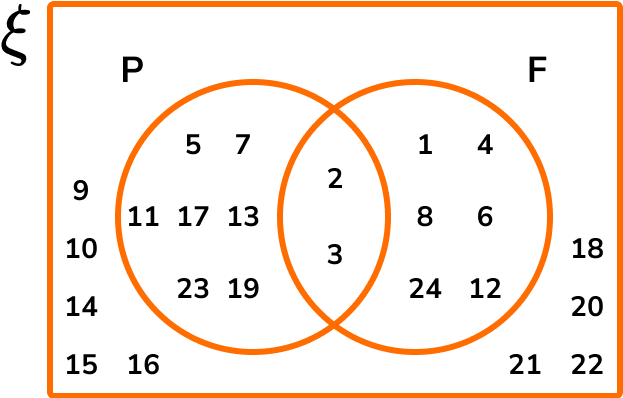
Determine the frequency of values in each box / section if required.
The question asks us for the frequency of values in set P, which is 9.
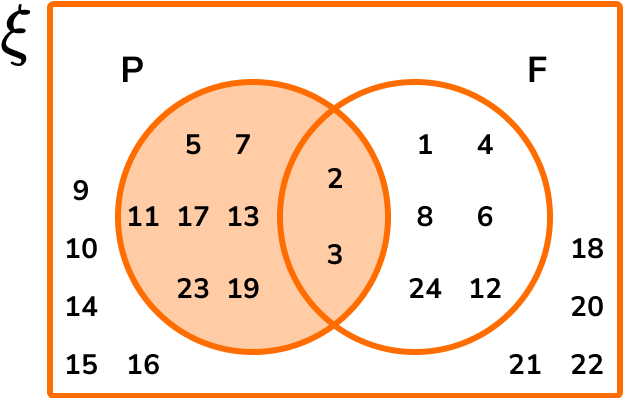
We are also asked to find the frequency of values in P \cap F which is the section ‘P and F’. There are 2 values in P \cap F.
Common misconceptions
- \bf{1} is not a prime number
1 is not a prime number. This is because it only has one factor, rather than the 2 factors needed to be a prime number.
- \bf{2} is a prime number
2 is the only even prime number. This is because it only has two factors, 1 and itself, and therefore by definition, it is a prime number. Every other even number is divisible by 2. \ 2 is therefore known as a special case when discussing prime numbers.
- Prime numbers and the odd numbers
As all but one of the prime numbers are odd (remember that 2 is the only even prime number), it is sometimes assumed that all odd numbers are prime. Take the number 9. It is an odd number, however 9 is a multiple of 3 and so we can divide 9 by 3 (and get 3 ). Not all odd numbers are prime, and not all prime numbers are odd.
- Decimals cannot be prime numbers
All prime numbers are positive integers but a common misconception is that decimals can be prime. For example, the decimal 2.3 is considered to be a prime number as 23 is a prime number.
Practice prime numbers questions
1. Determine what type of number 71 is from the list below.
Multiple of 3

Multiple of 4

Multiple of 5

Prime number

71 does not end in 0, 2, 4, 6 or 8 and so is not a multiple of 2. It cannot therefore be a multiple of 4.
7+1=4 so 71 is not a multiple of 3 .
71 does not end in 0 or 5 therefore it is not a multiple of 5.
71 \div 7=10.14 therefore it is not a multiple of 7.
This tells us that 71 is a prime number.
2. Determine what type of number 513 is from the list below.
Multiple of 2

Multiple of 3

Multiple of 5

Prime number

513 is a multiple of 3 as 5+1+3=9 which is a multiple of 3.
513\div{3}=171
3. Determine what type of number 143 is from the list below.
Multiple of 3

Multiple of 7

Multiple of 11

Prime

1+4+3=8 so 143 is not a multiple of 3 .
143\div 7=20.42857… so 143 is not a multiple of 7 .
143\div{11}=13 so 143 is a multiple of 11 .
4. Which number from the list is prime?
![]()




2 is the only even prime number. It has two factors, 1 and itself.
81 has factors of 1, 3, 9, 27 and 81.
343 has factors of 1, 7, 49 and 343.
3\times{10}^{2} written as an ordinary number is 300 which has many factors.
5. Let N=\{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\}. Which two way table correctly sorts the set N?








Factors of 12: 1, 2, 3, 4, 6, 12
Prime Numbers: 2, 3, 5, 7, 11

6. The Venn diagram below represents the two sets P=\{ Prime \} and F=\{ Factor of 10\}. Given that ξ= \{x is an integer such that 0 < x \leq 12 \}, work out the frequency of values that would appear in P \cap F.
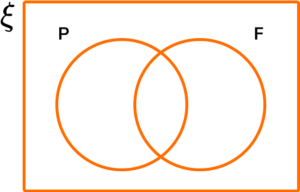


2 and 5


Factors of 10: 1, 2, 5, and 10.
Prime Numbers: 2, 3, 5, and 7.
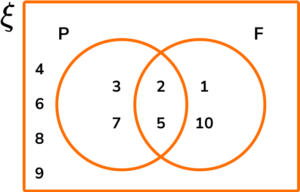
Each value placed correctly in the Venn diagram gives the result:
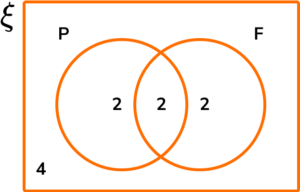
The frequency that corresponds to each set is therefore:
Prime numbers GCSE questions
1. (a) Write the first 8 prime numbers.
(b) Peter says “every prime number is odd”. Is Peter correct? Explain your answer.
(3 marks)
(a)
2, 3, 5, 7, 11, 13, 17, 19
(1)
(b)
No
(1)
2 is the only even prime number.
(1)
2. (a) The perimeter of a rectangle can be written as P=2(l+w) where l and w are integer side lengths.
Given that the area of the rectangle is 23cm^{2}, calculate the perimeter of the rectangle.
(b) A square has an area of A=x^{2}, where x is an integer. Is the area always, sometimes or never a prime number? Explain your answer.
(4 marks)
(a)
l=1 and w=23 or l=23 and w=1
(1)
P=2(23+1)=2\times{24}=48\text{cm}(1)
(b)
All square numbers have an odd number of factors, whereas all prime numbers have 2 factors.
or
1 is not prime and any other square number has a factor of its square root meaning it is not prime.
(1)
Never
(1)
3. Below is a list of numbers:
![]()
(a) Which of the values is a prime number?
(b) Which of the values is 2 more than a prime number, and 2 less than another prime number?
(c) Which of the values gives a prime number when it is squared?
(3 marks)
(a) 73
(1)
(b) 21
(1)
(c) \sqrt{5}
(1)
4. (a) On the Venn diagram below, P=\{ Prime numbers \} and M=\{ Multiples of 4\}.
For the set of numbers ξ=\{x such that 20 < x \leq 40 \}, complete the Venn diagram.
(b) Write down the numbers that are in the set P .
(c) How many numbers are in the set P \cap M?
(6 marks)
(a)
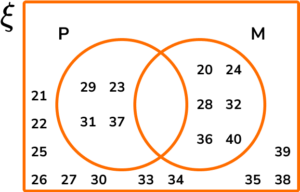
Prime Numbers: 23, 29, 31, 37.
(1)
Multiples of 4: 20, 24, 28, 32, 36, 40.
(1)
No values in the intersection (P \cap M).
(1)
(P \cup M)’: 21, 22, 25, 26, 27, 30, 33, 34, 35, 38, 39.(1)
(b) 23, 29, 31, 37
(1)
(c) 0
(1)
Learning checklist
You have now learned how to:
- Identify prime numbers
- Know and use the vocabulary of prime numbers, prime factors and composite (non-prime) numbers
- Establish whether a number up to 100 is prime and recall prime numbers up to 19
The next lessons are
The sieve of Eratosthenes
The ancient greek mathematician Eratosthenes of Cyrene lived nearly 2300 years ago. He devised a way of determining the prime numbers using the method that we know of today called the Sieve of Eratosthenes (or Eratosthenes Sieve).
Below is a number square from 1 to 100.
Our aim is to cross out every number that is not prime.
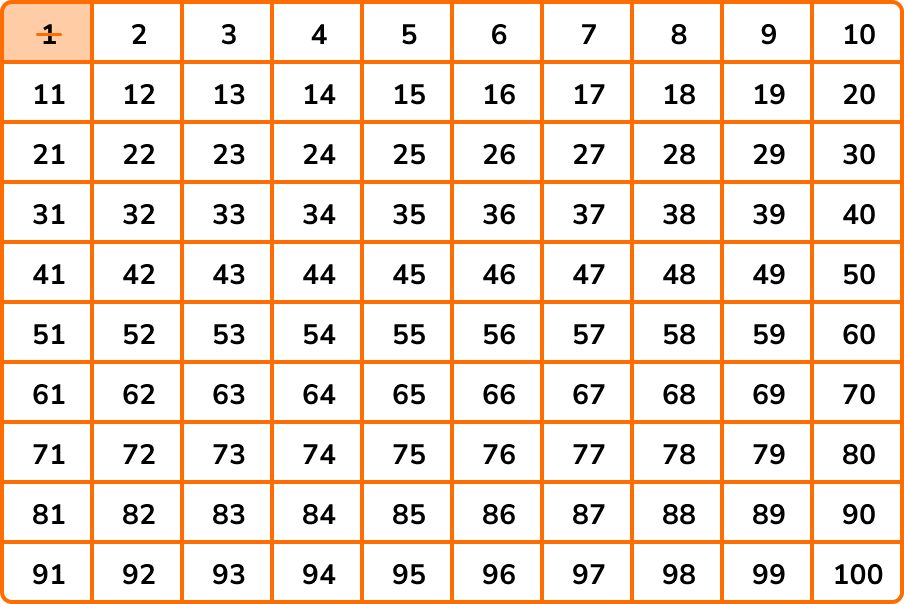
We start by crossing out the number 1 because a prime number has two factors, itself and 1, however the number 1 is itself and so by definition, 1 has only 1 factor and is therefore not prime.
Any number that is a multiple of 2 can divide by 2. The number 2 is prime because we can only divide 2 by 1 and 2 (itself).
All the other multiples of 2 have a factor of 2 and so we highlight 2, and then cross out all of the other multiples of 2 .
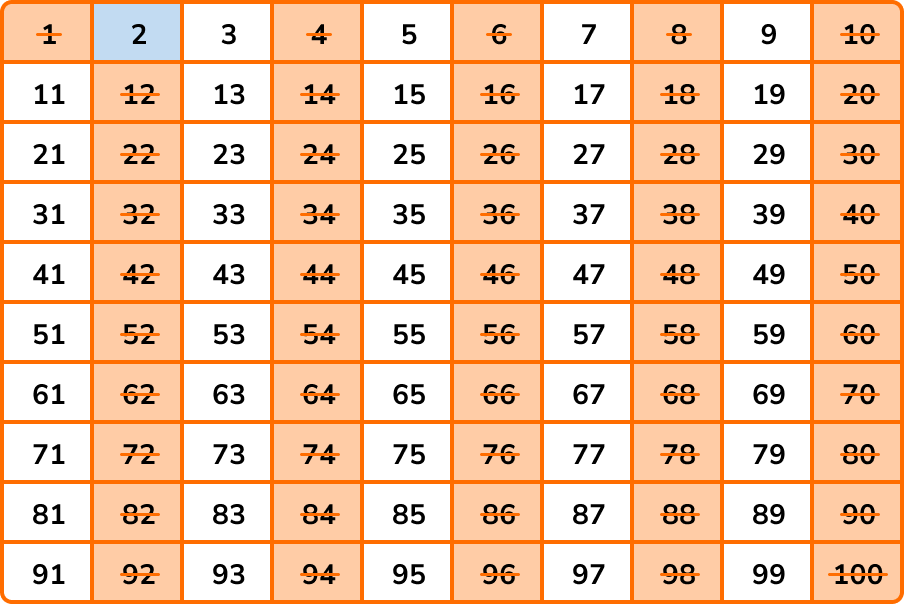
The next number that is not crossed out is 3. \ 3 is prime as we can only divide it by 1 and 3. All of the multiples of 3 have a factor of 3, and so we highlight 3, and cross out all of the other multiples of 3 .
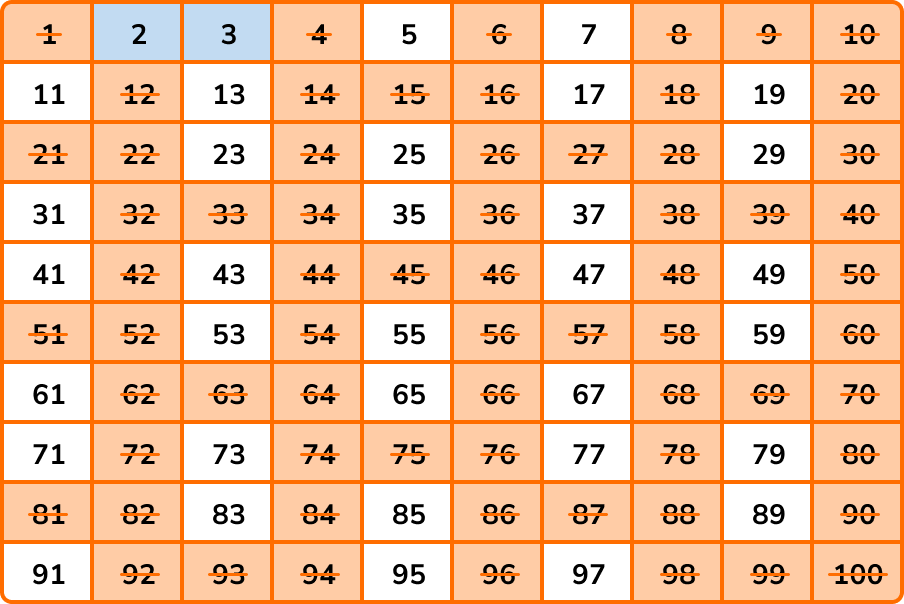
Continuing with the sieve of Eratosthenes, every multiple of 4 can be divided by 2, and so all of the multiples of 4 are already crossed out.
The next number that is not crossed out is 5. \ 5 is prime so we highlight 5 and cross out all of the other multiples of 5 .
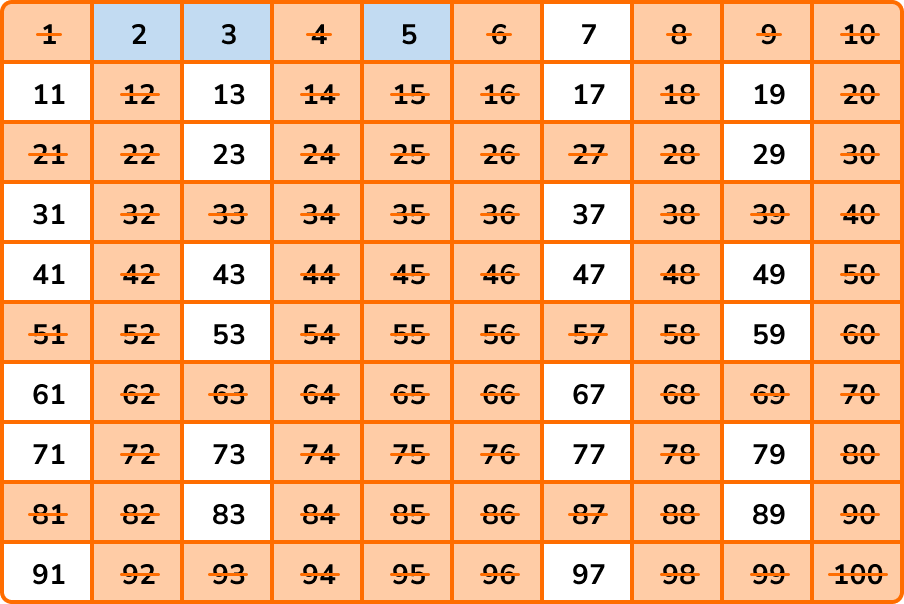
As we continue, the next number that is not crossed out will always be prime.
The next number in the list is a 7, so we highlight 7 and cross out the multiples of 7 .
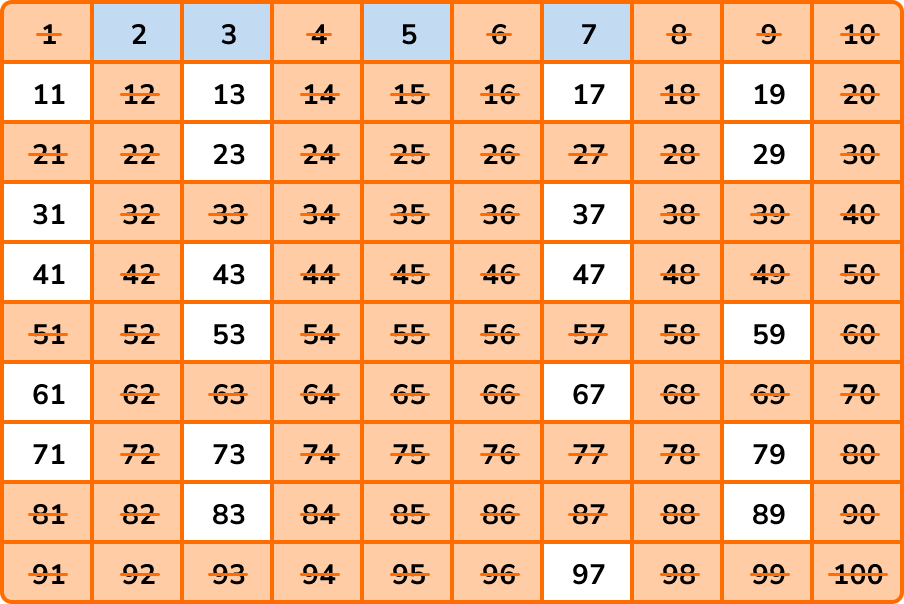
Amazingly, once you have crossed out the multiples of 7, all of the remaining numbers between 1 and 100 have no multiples that are not already crossed out between 1 and 100, and so we can highlight the rest of the numbers like this:
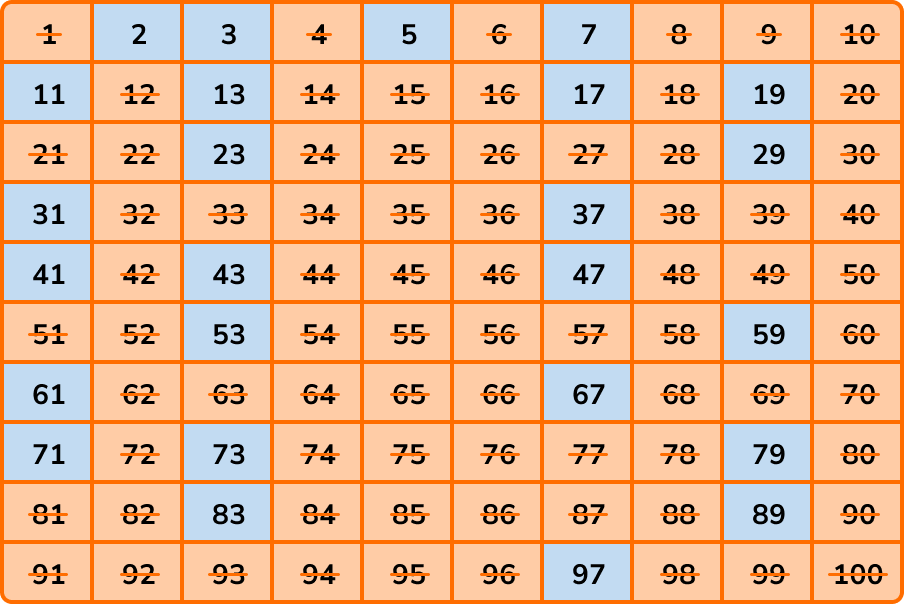
This leaves us with the list of prime numbers between 1 and 100 which are,
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97.
The downside to this method is that it is very time consuming, especially if you want to determine whether certain large numbers are prime numbers.
Other facts about prime numbers
The square root of any prime number is a surd.
Step-by-step guide: Surds
The ancient Egyptians are believed to be the first civilisation to recognise prime numbers. Today, prime numbers are considered to be the building blocks of mathematics as every number is itself prime, or can be built by multiplying two or more prime numbers together.
In number theory, the fundamental theorem of arithmetic states that any given number can be represented by a unique product of prime numbers. This is useful when we calculate prime factors of a number.
Step-by-step guide: Prime factors
The greek mathematician Euclid derived the Prime Number Theorem, which states that there are infinitely many prime numbers. Computers are used today to calculate large primes. In March 2022, the largest known prime number was 2^{82,589,933}-1 which has 24,862,048 digits! This number was found in 2018 by the great internet mersenne prime search. If there are an infinite number of prime numbers, the challenge is always to find the next largest prime number.
Prime numbers are used a lot in cryptology and cryptography. Cryptology is the process used to convert plaintext into ciphertext, and vice versa, whereas cryptography is just the conversion of plaintext to ciphertext. Public key cryptography utilises very large prime numbers within message encryption; you can only decode the message if you know the prime numbers and it is very difficult to calculate them.
A primality test is an algorithm that determines whether a number is prime. We used a form of primality test when using positive divisors to determine whether a number is prime.
A mathematical conjecture is an incomplete mathematical proof. Once a conjecture is fully proven, it is a theorem.
The twin prime conjecture, also known as Polignac’s conjecture asserts that there are infinitely many twin primes (pairs of primes that differ by 2 ) such as 3 and 5, 11 and 13, and 17 and 19.
Christian Goldbach in 1742 derived Goldbach’s conjecture. Goldbach’s conjecture states that any even whole number greater than 2 is the sum of two prime numbers.
A Fermat number or Fermat prime is a type of prime number. If 2^{k}+1 is a prime number and k > 0, then k is a power of 2. In March 2022, there are only 6 known Fermat primes: 3, 5, 17, 257, and 65537.
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.