One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
ArithmeticThis topic is relevant for:

Multiples
Here we will learn about multiples, including how to calculate multiples of a number, identify common multiples, and solve problems using knowledge of multiples.
There are also multiples worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What are multiples?
Multiples are the result of multiplying a number by an integer.
For example, the first 5 multiples of 7 are: 7, 14, 21, 28, and 35.
Multiples can be integers, decimals, fractions, negative numbers or surds, and can sometimes be called products.
The product of two or more factors is a multiple, and every integer is a multiple of two or more factors.
In general, if n is any number and x is an integer, m is a multiple of n where
n\times{x}=m .
To calculate a multiple of a number n , you have to multiply it by an integer. You can list multiples of a number by multiplying n by the position of the value in the list.
For example, the 9th multiple of 4 is equal to 9 \times 4=36.
What are multiples?

How to calculate multiples
In order to calculate multiples of a number n:
- State the first multiple of \textbf{n} .
- Calculate the second multiple of \textbf{n} .
- Continue until you have calculated the number of multiples needed.
- Write the solution.
Explain how to calculate multiples

Multiples worksheet

Get your free multiples worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Multiples worksheet

Get your free multiples worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on factors and multiples
Multiples is part of our series of lessons to support revision on factors and multiples and factors, multiples and primes. You may find it helpful to start with the main factors and multiples lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Multiples examples
Example 1: listing multiples (single digit number)
List the first 5 multiples of 8.
- State the first multiple of \textbf{n} .
The first multiple of 8 is
8\times{1}=8.2Calculate the second multiple of \textbf{n} .
The second multiple of 8 is
8\times{2}=16.3Continue until you have calculated the number of multiples needed.
\begin{aligned} &8\times{3}=24. \\\\ &8\times{4}=32. \\\\ &8\times{5}=40. \end{aligned}4Write the solution.
The first 5 multiples of 8 are 8, 16, 24, 32, and 40.
Example 2: listing multiples (decimal)
List the first 5 multiples of 1.2.
State the first multiple of \textbf{n} .
The first multiple of 1.2 is
1.2\times{1}=1.2.
Calculate the second multiple of \textbf{n} .
The second multiple of 1.2 is
1.2\times{2}=2.4.
Continue until you have calculated the number of multiples needed.
Write the solution.
The first 5 multiples of 1.2 are 1.2, 2.4, 3.6, 4.8, and 6.
Example 3: listing multiples (negative number)
List the first 5 multiples of -4.
State the first multiple of \textbf{n} .
The first multiple of -4 is
-4\times{1}=-4.
Calculate the second multiple of \textbf{n} .
The second multiple of -4 is
-4\times{2}=-8.
Continue until you have calculated the number of multiples needed.
Write the solution.
The first 5 multiples of -4 are -4, -8, -12, -16, and -20.
Example 4: calculate a specific multiple
What is the 9th multiple of 7?
State the first multiple of \textbf{n} .
You only need to calculate the 9th multiple of 7 so you can move on to step 2.
It is worth noting here that you are looking at the multiples of 7.
Calculate the second multiple of \textbf{n} .
Move on to step 3.
Continue until you have calculated the number of multiples needed.
The 9th multiple of 7 is equal to
7\times{9}=63.
Write the solution.
The 9th multiple of 7 is 63.
Example 5: calculate a specific multiple
What is the 4th multiple of -1.8?
State the first multiple of \textbf{n} .
As you only need to calculate the 4th multiple of -1.8, you can move on to step 2.
It is worth noting here that you are looking at the multiples of -1.8.
Calculate the second multiple of \textbf{n} .
Move on to step 3.
Continue until you have calculated the number of multiples needed.
The 4th multiple of -1.8 is equal to
-1.8\times{4}=-7.2.
Write the solution.
The 4th multiple of -1.8 is -7.2.
Example 6: common multiples
Given that the first 5 multiples of 8 are 8, 16, 24, 32, and 40, find a common multiple of 6 and 8.
State the first multiple of \textbf{n} .
The first multiple of 6 is
6\times{1}=6.
Calculate the second multiple of \textbf{n} .
The second multiple of 6 is
6\times{2}=12.
Continue until you have calculated the number of multiples needed.
Write the solution.
The first common multiple of 6 and 8 is 24.
Common misconceptions
- Factors and multiples
Factors and multiples are easily mixed up. Remember multiples are the multiplication table, whereas factors are the numbers that go into another number without a remainder.
- Remember the number itself for factors and multiples
All numbers are a multiple of themselves.
For example, the multiples of 6 are 6, 12, 18, 24 and so on and so 6 is a multiple of itself.
Practice multiples questions
1. List the first 5 multiples of 12.




So, the first 5 multiples of 12 are 12, 24, 36, 48, and 60.
2. List the first 5 multiples of 2.3.




So, the first 5 multiples of 2.3 are 2.3, 4.6, 6.9, 9.2, 11.5.
3. List the first 5 multiples of -6.




So, the first 5 multiples of -6 are -6, -12, -18, -24, and -30.
4. What is the 8th multiple of 9?




5. What is the 6th multiple of -2.5?




6. The first 6 multiples of 4 are 4, 8, 12, 16, 20 and 24. By calculating the multiples of 6, determine the first 2 common multiples of 4 and 6.




The first 5 multiples of 6 are 6, 12, 18, 24, and 30.
The first common factor of 4 and 6 is 12 and the second is 24.
Multiples GCSE questions
1. Below is a list of numbers,
2, \ 4, \ 5, \ 7, \ 8, \ 12, \ 15, \ 24 .
(a) Which numbers are multiples of 4?
(b) Which numbers are multiples of 3?
(c) Which numbers are 1 more than a multiple of 7?
(d) Which number is a multiple of two other numbers in the list?
(4 marks)
(a) 4, 8, 12, 24
(1)
(b) 12, 15, 24
(1)
(c) 8, 15
(1)
(d) 8\ ( = 2 \times 4)
(1)
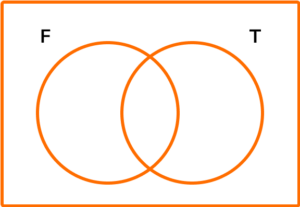
2. (a) The Venn diagram below shows the two sets F=\{ Multiples of 4\} and T=\{ Multiples of 10\}.
\xi=\{2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40\}
Place all of the numbers from this set on to the Venn diagram.
(b) What is the lowest common multiple of 4 and 10?
(3 marks)
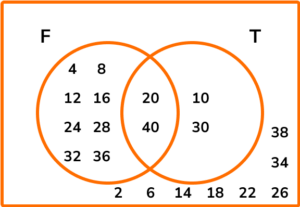
(a)
Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40
(1)
Multiples of 10: 10, 20, 30, 40
(1)
Completed Venn diagram
(1)
(b) 20
(1)
3. An ice cream stand sells vanilla ice cream in a single cone with raspberry sauce.
Single cones are sold in packs of 50.
Ice cream tubs contain 20 portions of ice cream.
A bottle of raspberry sauce serves 40.
Kevin wants to buy the same number of servings of ice cream, cones and raspberry sauce.
What is the smallest number of tubs of ice cream he would need to buy?
(3 marks)
Multiples of 50, 20 and 40 listed.
(1)
200 of each ingredient.
(1)
200\div{20}=10 tubs of ice cream.
(1)
Learning checklist
You have now learned how to:
- Find factors and multiples
- Write numbers as a product of their prime factors
- Find the lowest common multiple
- Find the highest common factor
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.