One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
This topic is relevant for:

Arithmetic
Here we will learn about arithmetic, including key terminology and mathematical symbols, using the four operations with positive and negative integers and inverse operations.
There are also arithmetic worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is arithmetic?
Arithmetic is the study of numbers and the operations between them. It is an elementary branch of mathematics. The definition of arithmetic originates from the Greek word arithmos, meaning number, or arithmētikē, the art of counting.
To solve problems using basic arithmetic, we need to understand and use four arithmetic operators. At GCSE, we need to be able to use these operations for both positive and negative integers (whole numbers), fractions and decimals.
The four types of computations we will be looking at are: addition, subtraction, multiplication and division.
What is arithmetic?

Mathematical symbols
Below is a table showing the four basic operations of arithmetic with their associated symbols.
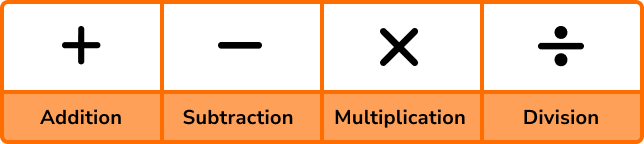
Each operation has a different function that you should already be confident with using.
Arithmetic with four operations
Addition
Addition combines elements in two or more sets together. For two sets a and b, the new set c is equal to the sum of a and b, written as a+b=c and pronounced a plus b is equal to c.
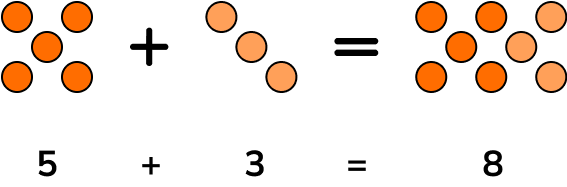
Addition is commutative. The order in which the calculation is carried out does not matter.
For example,
3+4=4+3=7Addition can be done with positive and negative integers, fractions and decimals. Addition represents a movement up the number line. Here are some examples,

In order to perform more difficult additions, we can use the column method.
For example, 347+21
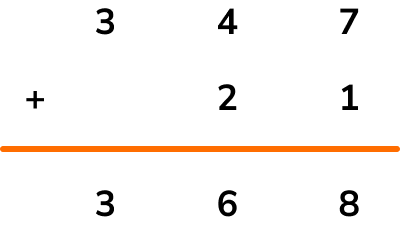
It is important to consider the place value of each digit and line up the corresponding digits in each number.
Subtraction
Subtraction removes elements from a set. The set of elements remaining when the elements in b are subtracted from the elements in c would be equal to a, written as c-b=a and pronounced c take away b is equal to a.
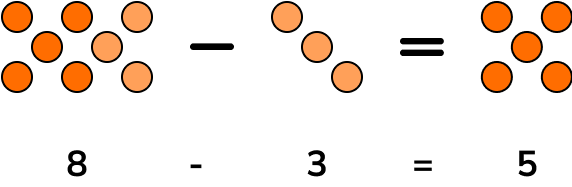
Subtraction is not commutative. If the order of the numbers within the calculation changes, the result will change.
For example,
7-4
Subtraction can also be done with positive and negative integers, fractions and decimals. Subtraction represents a movement down the number line. Here are some examples,

In order to perform more difficult subtractions, we can use the column method.
For example, 89.4-3.1

Multiplication
Multiplication is essentially repeated addition. If we have n copies of set a, we multiply a by n to find how many elements are in the new set, m. This is the same as calculating a+a+a+... \ n times. This would be written as n \times a=m and pronounced n times a is equal to m.

Multiplication is commutative. The order in which the calculation is carried out does not matter.
For example,
3\times{4}=4\times{3}=12Multiplication can also be done with positive and negative integers, fractions and decimals. When multiplying positive and negative numbers, the following rules apply,
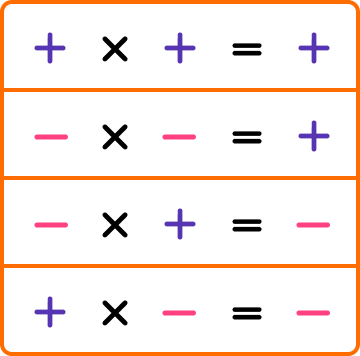
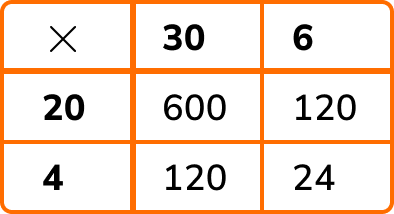
To perform more difficult multiplications, we can use the grid method.
For example, 27 \times 35
Division
Division shares the elements of a set into a number of distinct groups. If the elements of set m can be shared equally between n groups, with no remainder, then this is written as m\div{n}=a and pronounced m divided by n is equal to a.
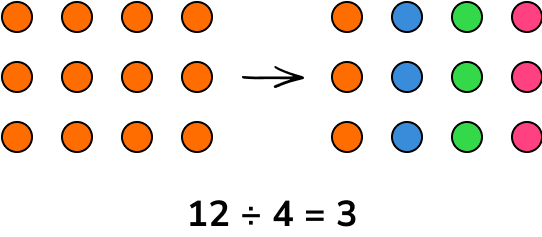
Unlike multiplication, division is not commutative. If the order of the numbers within the calculation changes, the result will change.
12\div{4}
Division can also be done with positive and negative integers, fractions and decimals. When dividing positive and negative numbers, the following rules apply,
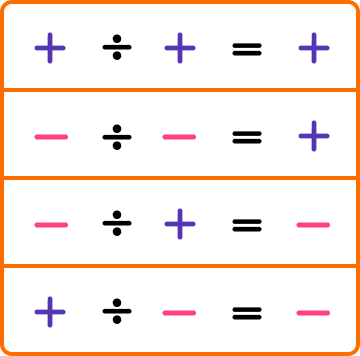
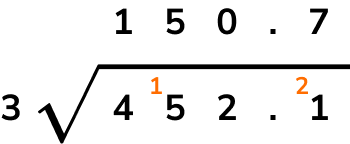
To perform more difficult divisions, we can use the method of short division.
For example, 452.1 \div 3
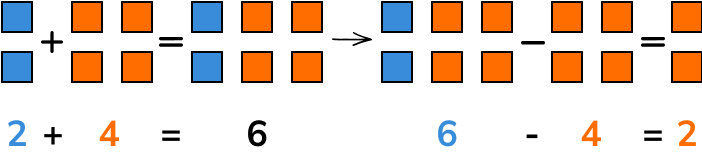
Inverse operations
Inverse operations reverse an operation that has been carried out. Below is a table outlining some operations along with their inverse operations.

Note that we can switch the columns so the inverse operation of subtraction is addition and the inverse operation of division is multiplication, etc.
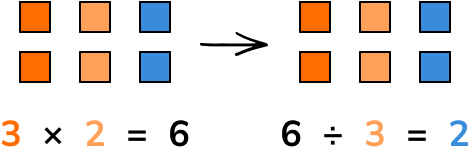
BIDMAS
When solving problems involving arithmetic operations, it is important to apply BIDMAS. BIDMAS tells us what order to perform operations in and stands for
Brackets
Indices
Division
Multiplication
Addition
Subtraction
In the calculation 3+4 \times 2, the multiplication should be done before the addition.
3+4 \times 2=3+8=11Step-by-step guide: BIDMAS
Quotients
The quotient is the answer we get when we divide one number by another.
The word quotient comes from Latin and means ‘how many times’. When we divide we are finding out ‘how many times’ a number goes into another number.
Dividend \div divisor = quotient
For example,
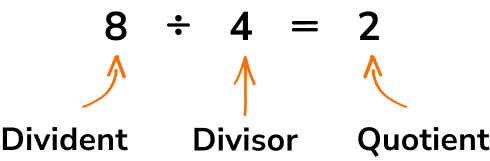
In this calculation, 8 is the dividend,
4 is the divisor and
the answer, 2 , is the quotient.
The quotient will only be 0 if the dividend is 0 but the divisor is not.
For example,
0 \div 8 = 0Word problems
At GCSE level, we are often presented with word problems that need to be worked out using arithmetic. The first step is to decide on which operation is required and then the relevant calculations can be performed. It can help to highlight important information in the questions.
Step-by-step guide: Money problems maths
See also: Calculator skills
How to use arithmetic with positive and negative numbers
In order to use arithmetic with positive and negative numbers:
- Determine which operator you need to use.
- Carry out the calculation.
Explain how to use arithmetic with positive and negative numbers

BIDMAS worksheet (includes arithmetic)

Get your free arithmetic worksheet of 20+ BIDMAS questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
BIDMAS worksheet (includes arithmetic)

Get your free arithmetic worksheet of 20+ BIDMAS questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREEArithmetic examples
Example 1: addition with decimals
Calculate the value of 10.9+34.3.
- Determine which operator you need to use.
Here we need to use addition.
2Carry out the calculation.
Rearranging the layout of the calculation into a column addition format, we have

Adding up the right hand column first we have 9+3=12. The tenths column value of 2 is therefore placed in the answer bar below the sum, and the 1 is carried across below the answer bar so that we can add it to the next column total (the units column).
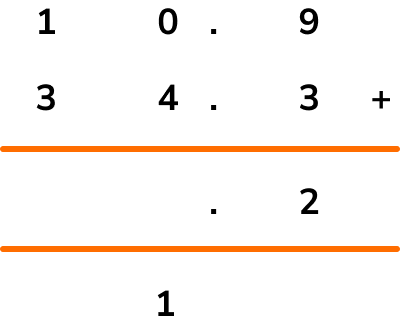
Adding 0, 4, and the 1 that was carried across from the tenths column, we have 0+4+1=5 and so 5 goes into the answer bar for the units column.
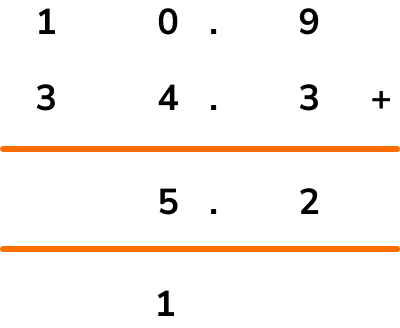
The final column requires us to add 1 and 3. \ 1+3=4 and so we put a 4 in the tens column.
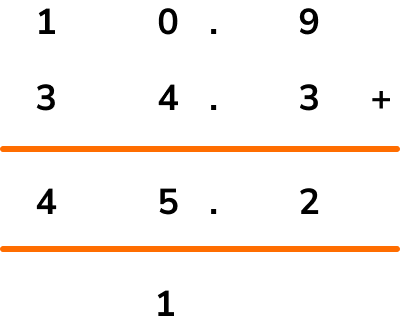
So 10.9+34.3=45.2 .
Example 2: subtraction (worded problem)
96 mathematicians attended a celebration party at a hotel. 38 mathematicians stayed overnight. How many mathematicians did not stay overnight?
Determine which operator you need to use.
Here we have a subtraction. We need to calculate 96-38.
Carry out the calculation.
Writing the subtraction using the column method, we have
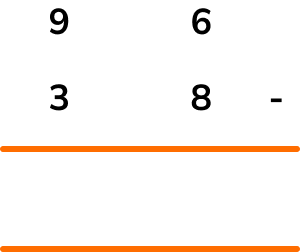
Starting from the units column, 6-8 is a negative number and so we have to borrow 1 from the tens column.
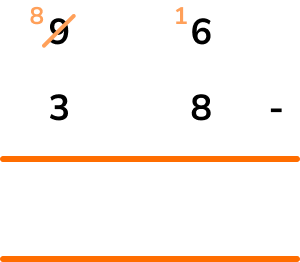
16-8=8 and so the value for the units column is 8.
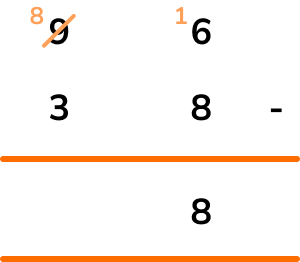
Continuing with the tens column, we have 8-3=5.
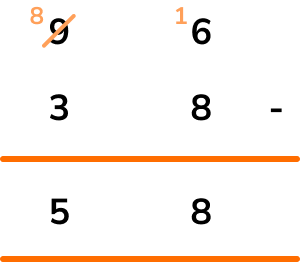
58 guests did not stay overnight.
Example 3: multiplication
Each sack contains 36 potatoes. A farmer packs 24 sacks of potatoes with no left over potatoes. How many potatoes does the farmer pack?
Determine which operator you need to use.
As we have 36 potatoes per sack and 24 sacks, we need to multiply these values together.
Carry out the calculation.
Using the grid method, we have
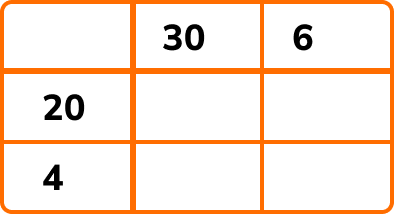
By multiplying each row value by each column value, we get
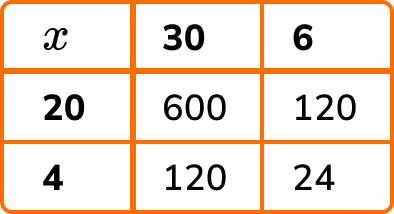
Adding the new values in the grid, we have
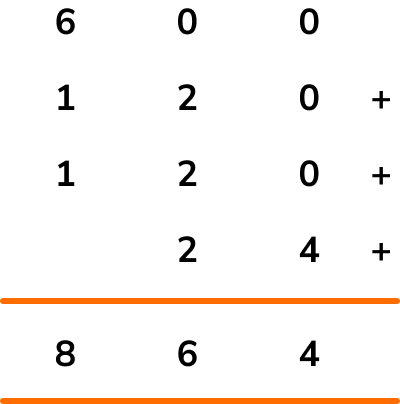
The farmer packs 864 potatoes.
Example 4: division
A bar of chocolate is made up of 84 individual cubes. The bar is 6 cubes wide. How many rows does the chocolate bar have?
Determine which operator you need to use.
As each column contains 6 cubes and there are 84 cubes in total, we need to divide 84 by 6 to determine the number of rows in the chocolate bar.
Carry out the calculation.
Using long division, we have

8\div{6}=1 remainder 2 and so we place the 1 above the 8 on the answer line, and carry the 2 across in front of the 4 to determine the units.
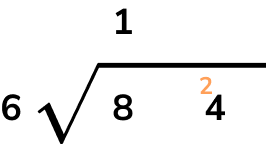
24\div{6}=4 with no remainder and so we write 4 on the answer line.
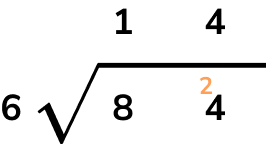
The chocolate bar has 14 rows.
Example 5: addition, with negative numbers
Calculate (-3)+(-2).
Determine which operator you need to use.
Here, we are calculating an addition with the two negative numbers.
Carry out the calculation.
+ and - together make a - therefore
-3 + -2= -3 -2 = -5 .
Example 6: subtraction, with negative numbers
Calculate 5-(-3).
Determine which operator you need to use.
Here we are subtracting -3 from 5.
Carry out the calculation.
Two - signs together make a + therefore
5--3=5+3=8 .
Example 7: multiplication, with negative numbers
Calculate 8\times(-2).
Determine which operator you need to use.
Here we are using a multiplication.
Carry out the calculation.
Example 8: division, with negative numbers
Calculate \frac{-120}{-3}.
Determine which operator you need to use.
A fraction is the division of two quantities and so here we are calculating a division. The numerator is known as the dividend and the denominator is known as the divisor. The result of a division is called a quotient.
Carry out the calculation.
Common misconceptions
- Brackets are not an arithmetic operator
Operators allow us to perform calculations between two or more numbers. Brackets dictate the order in which this should be completed and so they are technically not an operator.
- Multiplying by \bf{0}
It is important to remember that multiplying anything by 0 gives the answer 0.
- Dividing or multiplying by a fraction
Mistakes can easily be made when multiplying and dividing fractions. When dividing a number by a fraction, a commonly seen error is that the value is multiplied by the fraction instead. For example, 12\div\frac{1}{2}=6 is incorrect. Instead, the correct answer is 12\div\frac{1}{2}=12\times{2}=24.
Practice arithmetic questions
1. Calculate 8.4+10.7.





2. I bought an item for £25.13. How much change did I get from £30?





3. Calculate the 7th multiple of 9.




We need to multiply 9 by 7.
9\times{7}=63
4. 120 students are divided into small research groups. How many students are in each group if there are 20 groups?




We need to calculate 120 divided by 20.
120\div{20}=12\div{2}=6
5. A hotel comprises 67 floors above ground and 4 floors below ground. A guest parks on floor -3, in the basement, and is staying on the 43rd floor of the hotel. How many floors must he go up to get from his car to his hotel room?




This is a subtraction of 43 and -3.
43- -3=43+3=46
6. Anna buys a car worth £9,000. She pays a deposit of £2400 and pays the rest off in monthly instalments of £110 per month. For how many months will Anna be paying for her car?
104 months

22 months

60 months

66 months

This calculation requires a subtraction to calculate the remaining amount to pay for the car, and then a division of the remaining amount by 110.
9000-2400=6600
6600\div{110}=60
Arithmetic GCSE questions
1. Below is the advert board for a range of speciality teas.

(a) Calculate the total price of 2 green teas, 1 english breakfast tea, and 1 chamomile tea.
(b) Calculate the change from £10 for the order in part (a).
(4 marks)
(a)
2+2+2.10+2.25
(1)
£8.35(1)
(b)
10-\text{their } 8.35
(1)
£1.65(1)
2. (a) Simon says “ 16 divided by a half is 8 ”. Is Simon correct? Explain your answer.
(b) Stephanie says “ 7 \times 0=7 ”. Is Stephanie correct? Explain your answer?
(4 marks)
(a)
No
(1)
16\div{1}{2}=16\times{2}=32(1)
(b)
No
(1)
Any number multiplied by 0 is equal to 0 .
(1)
3. The number of worms in a population doubles every 3 weeks. The number of worms in a garden now is 120. How many worms will be in the garden in 12 weeks?
(3 marks)
Doubles 4 times.
(1)
120\times{2}\times{2}\times{2}\times{2}(1)
1920(1)
Learning checklist
You have now learned how to:
- Combine knowledge of number facts and rules of arithmetic to solve mental and written calculations
- Solve a wider range of problems, including increasingly complex properties of numbers and arithmetic
- Recognise arithmetic sequences
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.