One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
Arithmetic Place value Fractions, decimals and fractions Ratio Percentages Conversion of unitsThis topic is relevant for:

Money Problems Maths
Here we will learn about money problems maths, including looking at a variety of money word problems and how to solve them.
There are also money problems maths worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What are money problems?
Money problems are the name given to a range of problems which involve money. It may also be known as financial maths.
We will explore different types of money problems that can be used in lots of different situations.
For the purposes of these examples we will use Pound Sterling.
Remember,
£1 is made of 100 pence (or 100p ).
Pounds can be written as pence, for example £3.15 can be written as 315p.
Pence can be written as pounds, for example 27p can be written as £0.27.
UK coins are 1p, 2p, 5p, 10p, 20p, £1 and £2.
The UK notes are £5, £10, £20 and £50.

What are money problems?

How to work out money problems
In order to solve money problems in maths:
- Read the question carefully and work out how to solve the word problem.
- Calculate the solution.
- Write the answer with the correct units.
Explain how to work out money problems

Money problem maths worksheet
Get your free money problem maths worksheet of 20+ questions and answers. Includes reasoning and applied questions.
COMING SOONMoney problem maths worksheet
Get your free money problem maths worksheet of 20+ questions and answers. Includes reasoning and applied questions.
COMING SOONRelated lessons on arithmetic
Money problems maths is part of our series of lessons to support revision on arithmetic. You may find it helpful to start with the main arithmetic lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Money problem maths examples
Example 1: shopping
A chocolate bar costs 45p and a bottle of lemonade costs £1.20.
Frankie buys 3 bars of chocolate and 2 bottles of lemonade.
She pays with a £5 note.
Work out how much change Frankie gets.
- Read the question carefully and work out how to solve the word problem.
We need to find the total cost of 3 chocolate bars and 2 bottles of lemonade. Then subtract from £5 to find the change. But first we need to change 45p into £0.45.
2Calculate the solution.
The total cost is,
3\times 0.45 + 2\times 1.20=1.35+2.40=3.75Then we need to find the change,
5-3.75=1.25 .
3Write the answer with the correct units.
Frankie’s change is £1.25.
Example 2: ratio
Ali and Ben share some money in the ratio of 4:7. If Ben receives £10.50 more than Ali, work out the amount of money Ali receives.
Read the question carefully and work out how to solve the word problem.
We have been given the difference in the amount of money Ali and Ben receive.
Looking at the ratio, the difference in parts is 3 parts,
7-4=3.
We can divide the difference by 3 and find the size of each part. Then we can work out how much money Ali gets.
Calculate the solution.
One part is
10.50\div 3=3.50.
Ali gets four parts,
3.50\times 4=14.
Write the answer with the correct units.
Ali receives £14.
Note that Ben receives £24.50, so £10.50 more, and the total money shared was £38.50.
Example 3: fractions
A laptop costs £350. A sale offers \frac{1}{5} off the price. Calculate the sale price of the laptop.
Read the question carefully and work out how to solve the word problem.
We have to find one fifth of the cost, and subtract it.
Calculate the solution.
First we find the fraction of the amount.
350\div 5 = 70.
So \frac{1}{5} of 350=70.
Then we subtract this from the original price,
350-70=280.
Write the answer with the correct units.
The new price of the laptop is £280.
Example 4: percentage increase
A railcard costs £430. The price is going up by 23\%. Calculate the new price of the railcard.
Read the question carefully and work out how to solve the word problem.
We need to find 23\% of the amount and add it on.
Calculate the solution.
Therefore 23\% will be
(2\times 43)+(3\times 4.30)=86+12.90=98.90.
Because the question wants an increase, we add this to the original amount.
430+98.90=528.90
Write the answer with the correct units.
The final answer for the new price of the rail card is £528.90.
Alternatively you could use a multiplier,
430\times 1.23=528.90.
Example 5: best buy
Cereal can be bought in two different ways.
A small box contains 200g and costs 89p.
A large box contains 700g and costs £3.45.
Find which box is the best value for money.
Read the question carefully and work out how to solve the word problem.
There are several ways we can find out which cereal box gives the best value for money. We could work out grams per pence by dividing the mass by the price.
First we need to make sure both prices are in the same units. Let’s change the £3.45 into 345p.
Calculate the solution.
Small box – grams per pence,
200\div 89=2.24719…
Large box – grams per pence,
700\div 345=2.02898…
Write the answer with the correct units.
2.24719… grams per pence is greater than 2.02898… grams per pence. This means that when you buy the small box, you get more cereal per penny you spend.
Therefore the small box is better value for money.
Example 6: exchange rates
Sofia went to Portugal. She changed £160 into euros (€).
The exchange rate was £1 = €1.17.
How many euros did Sofia receive?
Read the question carefully and work out how to solve the word problem.
We need to use the exchange rate and multiply the amount in pounds to get the amount in euros.
Calculate the solution.
Write the answer with the correct units.
The solution is €187.20.
Common misconceptions
- Use two decimal places for pence
You might be asked to leave your answer in terms of pounds and pence. If your answer is 3.4, write it as £3.40, using two decimal places to represent the pence part.
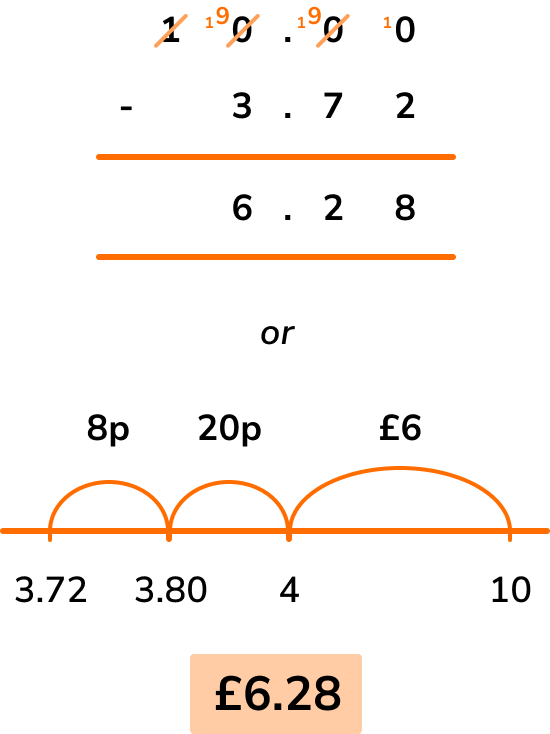
- Subtracting from \bf{£5, \ £10} and so on
Finding the change from paying with notes can be tricky if you are not using a calculator because of the zeros involved. You may wish to use a number line instead and count on.
For example, finding the change from £10 for a 3.72 shopping bill.
Practice money problems maths questions
1. A bottle of cola costs £1.35 and a bag of crisps costs 70p. Lamia buys 3 bottles of cola and 5 bags of crisps. She pays with a £10 note. Calculate the change Lamia gets.




70p written as pounds is £0.70. The total cost is
3\times 1.35+5\times 0.70=4.05+3.50=7.55.
The change can be found by subtracting the total cost from 10,
10-7.55=2.45.
The change is £2.45.
2. Sharon and Tania share a bill in the ratio of 5:3. If Tania pays £38 less than Sharon, what is the total amount of the bill?




The difference in the ratio parts is
5-3=2.
The difference is £38, since this is equivalent to two parts it is divided by 2.
38\div 2=19.
One part is £19.
The total number of parts is
5+3=8.
Therefore the total amount of money for the bill is
8\times 19=152.
3. A coat costs £60. A sale offers \frac{1}{4} off the price. Calculate the sale price of the coat.




We can find the fraction of the amount and then take it away from the original price.
\begin{aligned} &60\div 4=15 \\\\ &\frac{1}{4} \text{ of } £60 =£15 \\\\ &60-15=45 \end{aligned}
The sale price of the coat is £45.
4. A football season ticket costs £970. The price is being reduced by 15\%. Find the new price of the football season ticket.




We can find 15\% of £970, and then, because the price is decreasing, we can subtract it from the original price.
\begin{aligned} 100\%&=\pounds970\\\\ 10\%&=\pounds97\\\\ 5\%&=\pounds48.50 \end{aligned}
Therefore 15\% is
97+48.50=145.50.
The new price will be
970-145.50=824.50.
5. A large box of washing powder costs £4.85 for 950g.
A small box costs 55p for 100g.
Work out which box gives better value for money.
Large box, as 1.958 grams per pence is better value than 1.818 grams per pence.

Large box, as 0.51 grams per pence is better value than 0.55 grams per pence.

Small box, as 1.818 grams per pence is better value than 1.958 grams per pence.

Small box, as 0.51 grams per pence is better value than 0.55 grams per pence.

There are different ways to work out the best value. One way is to calculate grams per pence and see which gives the highest value.
Large box grams per pence,
950\div 485=1.958…
Small box grams per pence,
100\div 55=1.818…
The large box gives a greater amount of grams per pence, so is better value.
6. Ranjeev goes to Australia. He changes £325 into Australian dollars (\$). The exchange rate is £1 = \$1.74. Exchange £325 into Australian dollars.




As we are converting pounds to dollars, we need to multiply by the exchange rate.
325\times 1.74=565.50
Money problems maths GCSE questions
1. 2 apples and 3 bananas cost £1.40.
5 apples cost 95p.
Work out the cost of 3 apples and 4 bananas.
Give your answer in pounds and pence.
(3 marks)
(1)
\begin{aligned} &140-(2\times 19)=102 \\\\ &102\div 3=34 \end{aligned}(1)
(3\times 19)+(5\times 34)=57+170=227=\pounds2.27(1)
2. Mike is going shopping for clothes for a new job. He has £150 to spend.
He buys 3 pairs of trousers for £29 each. He sees shirts cost £12 each.
Work out the maximum number of shirts Mike could buy.
(3 marks)
(1)
150-87=63(1)
63\div 12=5.25
So 5 shirts is the most he can buy.
(1)
3. Jonathan went to America.
He exchanged £750 into American dollars (\$).
The exchange rate was £1 = \$1.23.
(a) Exchange £750 into American dollars. Give your answer to the nearest 10 dollars.
(b) Jonathan brings \$147 back home.
Exchange \$147 into UK pounds.
Give your answer correct to the nearest pence.
(4 marks)
(a)
750\times 1.23=922.50
(1)
\$922.50 is \$920 to the nearest 10.
(1)
(b)
147\div 1.23=119.51219…
(1)
£119.51(1)
Learning checklist
You have now learned how to:
- Solve real world maths problems involving money
- Money problem solving with ratios, fractions and percentages
- Use exchange rates to convert currencies
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.