One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
Plotting graphs Simplifying fractions Negative numbers Scale mathsThis topic is relevant for:

Gradient Of A Line
Here we will learn about the gradient of a line, including how to find the gradient of a line from a graph, and from two coordinates, and state the equations of horizontal and vertical lines.
There are also worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is the gradient of a line?
The gradient of a line is the measure of the steepness of a straight line.
The gradient of a line can be either positive or negative and does not need to be a whole number.
The gradient of a line can either be in an uphill (positive value) or downhill direction (negative value).
What is the gradient of a line?
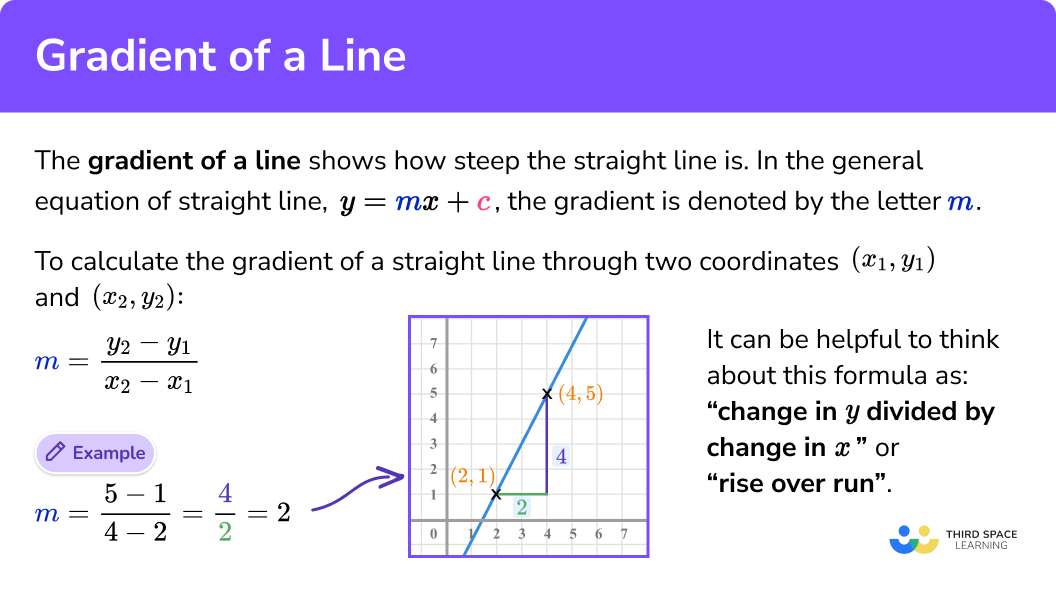
What is the gradient of a straight line?
The gradient formula of a straight line shows us how steep the line is. In the general equation of a straight line,
To calculate the gradient of a straight line through two coordinates (
How to understand the gradient of a line
Imagine walking up a set of stairs. Each step has the same height and you can only take one step forward each time you move. If the steps are taller, you will reach the top of the stairs quicker, if each step is shorter, you will reach the top of the stairs more slowly.
Let’s look at sets of stairs,
The blue steps are taller than the red steps and so the gradient is steeper (notice the blue arrow is steeper than the red arrow).
The green steps are not as tall as the red steps so the gradient is shallower (the green arrow is shallower than the red arrow).
Gradients can be positive or negative but are always observed from left to right.
The linear relationship between two variables can be drawn as a straight line graph and the gradient of the line calculates the rate of change between the two variables.
Currency gradient example
When calculating the exchange rate of two currencies, we can calculate the gradient of the line to find the rate of change between them.
Here, the exchange rate between pounds ( £ ) and dollars ($) is equal to \frac{3}{5}
Gradient formula
The gradient formula is a way of expressing the change in height using the
So using the gradient formula to find the gradient of a straight line given the two coordinates (
- The change in
x is the difference between thex coordinates:x₂ − x₁ - The change in
y is the difference between they coordinates:y₂ − y₁
This gives us a gradient formula of:
It can be helpful to think about this formula as:
‘Change in
Or
‘Rise over run’
Gradient equation
The gradient equation is another way we refer to the gradient of a straight line using
How to find the gradient of a line
To find the gradient of line you divide the change in height (
For example on a straight line with points
Gradient of diagonal lines
Let’s have a closer look at the gradient of
- When
m = 1 , for each unit square we move to the right, we move1 unit square upwards. - When
m = 2 , for each unit square we move to the right, we move2 unit squares upwards. - When
m = −3 , for each unit square we move to the right, we move3 unit squares downwards. - When
m = ½ , for each unit square we move to the right, we move½ a unit square upwards.
How far apart do the coordinates we choose need to be?
Let’s look at the example of
- The first blue line has a gradient of
- The second blue line has a gradient of
- The third blue line has a gradient of
No matter how far apart the coordinates are on the line, the resultant value will always simplify to the same number, here
Top tip: Use two coordinates that cross the corner of two grid squares so that you can accurately measure the horizontal and vertical distance between them. Use integers as much as possible!
Remember: the change in
Gradient of horizontal and vertical lines
There is no relationship between
Let us look at a couple of examples to further understand the equations of horizontal and vertical lines.
Example 1
In the diagram above, all the coordinates share an
Notice the line crosses the
Example 2
In the diagram above, all the coordinates share a
Notice the line crosses the
How to calculate the gradient of a line
In order to calculate the gradient of a line:
- Select two points on the line that occur on the corners of two grid squares.
- Sketch a right angle triangle and label the change in
y and the change inx . - Divide the change in
y by the change inx to findm .
Explain how to calculate the gradient of a line


Gradient of a line worksheet

Get your free gradient of a line worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Gradient of a line worksheet

Get your free gradient of a line worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on straight line graphs
Gradient of a line is part of our series of lessons to support revision on straight line graphs. You may find it helpful to start with the main straight line graphs lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Gradient of a curve
We can estimate the gradient of a curve at a given point by drawing a tangent line at that point and calculating its gradient.
A tangent line touches the curve at one point only. For the purposes of GCSE Maths, the tangent line is an estimate drawn by eye, but you should try to be as accurate as possible.
Once the tangent line has been drawn in, use the method described above to calculate the gradient of the tangent line. This gives an approximation or estimate for the gradient of the curve at that point.
For example,
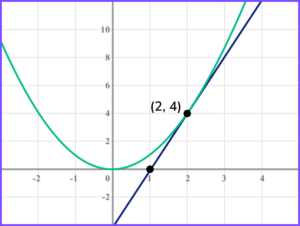
In the example above, the red curve is the equation y=x^{2} and the blue tangent line has been drawn to estimate the tangent at the point (2, 4).
Using the points (3, 8) and (2, 4) which both lie on the tangent line, we calculate \frac{\text { change in } y}{\text { change in } x}=\frac{4}{1}=4. Hence the gradient at the point (2, 4) is 4.
Gradient of a line examples
Example 1: using a straight line graph (positive gradient)
Calculate the gradient of the line:
- Select two points on the line that occur on the corners of two grid squares.
2Sketch a right angle triangle and calculate the change in y and the change in x.
3Divide the change in y by the change in x to find m.
Here,
so
Example 2: using a straight line graph (negative gradient)
Calculate the gradient of the line:
Select two points on the line that occur on the corners of two grid squares.
Sketch a right angle triangle and calculate the change in y and the change in x.
Remember the height of the triangle represents the change in
Looking at the coordinate (
Although the height of a triangle is always positive, we are calculating the change in
Divide the change in y by the change in x to find m.
Here,
so
Example 3: Using a straight line graph with two coordinates (positive gradient)
Calculate the gradient of the line:
Select two points on the line that occur on the corners of two grid squares.
Here we already have this information, so we can continue on with step
Sketch a right angle triangle and calculate the change in y and the change in x.
Divide the change in y by the change in x to find m.
Here,
so
Example 4: using a straight line graph with two coordinates (negative gradient)
Calculate the gradient of the line:
Select two points on the line that occur on the corners of two grid squares.
Here we already have this information, so we can continue on with step
Sketch a right angle triangle and calculate the change in y and the change in x.
Here we have to be careful because each grid square has a width of
Divide the change in y by the change in x to find m.
Here,
so
Example 5: given two coordinates (positive gradient)
Calculate the gradient of the line with coordinates
Select two points on the line that occur on the corners of two grid squares.
Here we have the two coordinates
Sketch a right angle triangle and calculate the change in y and the change in x.
As there is no right angle to sketch, we will solve algebraically by calculating the change in
Top tip: make sure you always subtract one coordinate from the other. Here we subtracted the values from coordinate
Divide the change in y by the change in x to find m.
Example 6: given two coordinates (negative gradient)
Calculate the gradient of the line with coordinates
Select two points on the line that occur on the corners of two grid squares.
Here we have the two coordinates
Sketch a right angle triangle and calculate the change in y and the change in x.
As there is no right angle to sketch, we will solve algebraically by calculating the change in
Divide the change in y by the change in x to find m.
Common misconceptions
- Mixing up the coordinates
A common error is to mix up the coordinates when calculating the change in
It is helpful to label each coordinate (
The change in
The change in
- Incorrect simplifying of
m (negative number division)
When you subtract one coordinate from another, one or both of the numerator and the denominator can be negative. If one is negative, the gradient is negative.
If both are negative, remember a negative number divided by another negative number is a positive number, so the gradient is positive.
E.g.
- Change in
x divided by the change iny
It is easy to mistake the calculation of
- Reading scales incorrectly
Sometimes the scale of the axis can change, e.g.
Practice gradient of a line questions
1. Calculate the gradient of the line:




\\m=\frac{2}{5}\\
2. Calculate the gradient of the line:




\\m=\frac{-9}{14}\\
3. Calculate the gradient of the line given the coordinates:




\\m=\frac{8}{6}=\frac{4}{3}\\
(each square on the x-axis is 2 units)
4. Calculate the gradient of the line given the coordinates:




\\m=\frac{-3}{6}\\
(each square on the x-axis is \frac{1}{2} unit)
5. Calculate the gradient of the line given the coordinates A(2,6) and B(8,24)




6. Calculate the gradient of the line given the coordinates A(-3,-8)) and B(-5,10)




Gradient of a line GCSE questions
1. Two straight line graphs A and B are shown on a set of axes. The equation of line A is y=2(x+1).
Use this information to calculate the gradient of the line B.
(4 marks)
The y -intercept of line A = 2 or (0,2) labelled
(1)
Each square on the x-axis is 1 unit, on the y -axis is 2 units:
(1)
Two coordinates selected on line B with correct change in y and change in x , e.g:
The change in y is -8 , and the change in x is 4
(1)
\\m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-8}{4}=-2\\
(1)
2. (a) Write an equation in the form y=mx+c that has the same gradient as the line 3y+9=12x.
(b) Tick the statements that are true for the equation 3y+9=12x and your solution for part a).
They are parallel
They intersect at the coordinate (0,-3)
They are perpendicular to one another
(4 marks)
(a)
(1)
m=4
(1)
Any equation of the form y=4x+c
E.g.
y=4x, y=4x+7, y=4x-8.
(1)
(b)
They are parallel ✔
They intersect at the coordinate (0,-3)
They are perpendicular to one another
(1)
3. Craig is calculating the gradient of the straight line shown below.
Here is Craig’s working:
Is Craig correct? Explain your answer.
(3 marks)
No (with reasoning)
(1)
The change in x is equal to:
-6–2=-6+2=-4
whereas Craig has stated the height of the triangle as 4
(1)
The gradient
\\m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{-4}{8}=-\frac{1}{2}\\
whereas Craig has incorrectly calculated
\\m=\frac{x_{2}-x_{1}}{y_{2}-y_{1}}\\
(1)
Learning checklist
You have now learned how to:
- Calculate and interpret gradients of graphs of such linear equations numerically, graphically and algebraically
- Interpret the gradient of a straight line graph as a rate of change
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.