One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
2D shapes Rounding numbers Arithmetic Substituting numbers into formulae Converting metric units BIDMASThis topic is relevant for:

Area
Here we will learn about area, including how to calculate the area of triangles, quadrilaterals, circles and compound shapes.
There are also area worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is area?
Area is a measure of the amount of space there is inside a 2D shape. The area of a shape is measured in square units such as cm^{2}, mm^{2} or m^{2}.
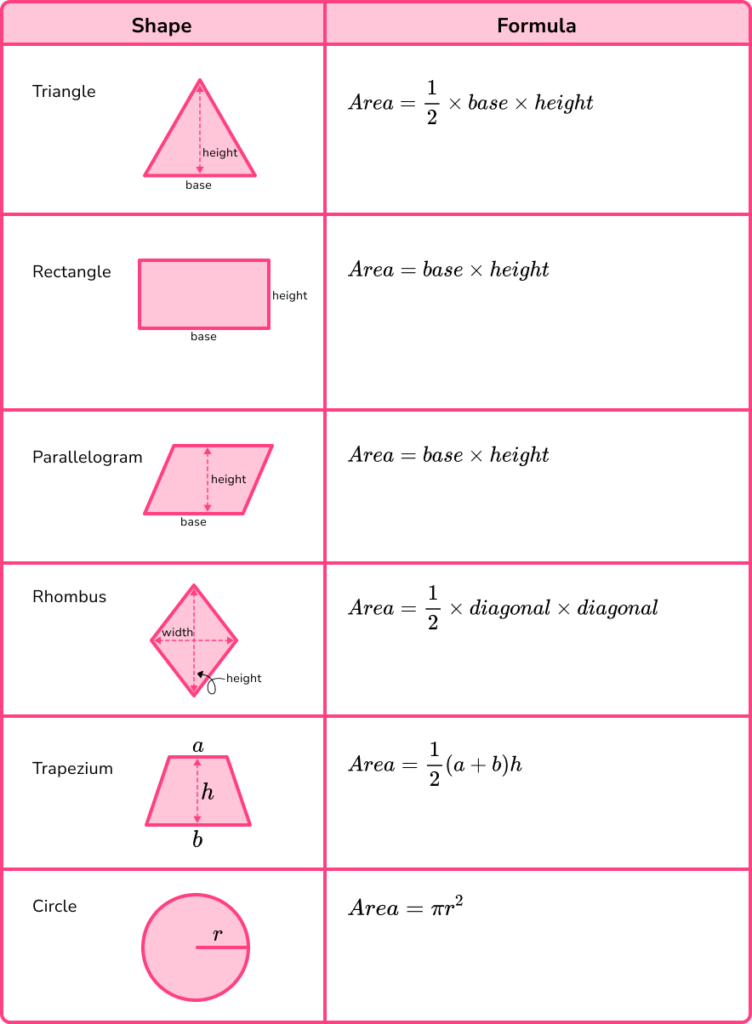
To calculate area we can use different formulas depending on the shape.
Below are the formulas to find the area of some common shapes. For each of the shapes below there are also pages where you can see more examples.
Step-by-step guide: How to work out area
We can also find the area of polygons and compound shapes using a combination of these formulas.
A compound shape can be split into two or more smaller shapes and the area of these shapes can be found. The total area of the compound shape can be found by adding the smaller areas together.
Here are some examples of compound shapes.
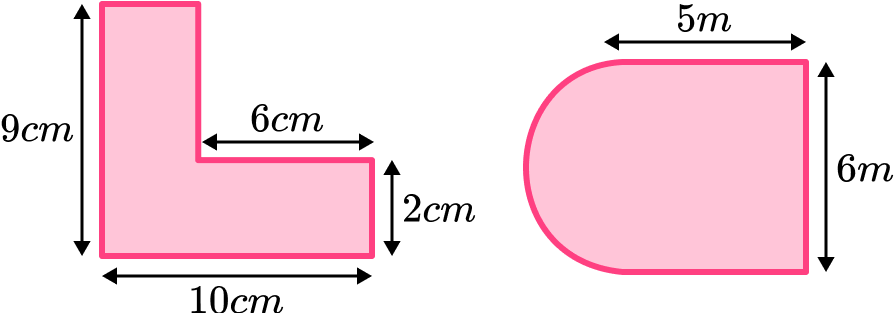
Step-by-step guide: Area of compound shapes
What is area?
How to calculate area
In order to calculate the area of a shape:
- Write down the formula for the area of the shape.
- Identify the values required for the formula.
- Substitute the values and calculate.
- Write down your final answer with units squared.
Explain how to calculate area

Area worksheet

Get your free area worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Area worksheet

Get your free area worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREEArea examples
Example 1: area of a rectangle
Find the area of this rectangle below.

- Write down the formula for the area of the shape.
Rectangle,
\text { Area }=\text { base } \times \text { height } .
2Identify the values required for the formula.
Base = 7m
Height = 4m
3Substitute the values and calculate.
\begin{aligned} \text { Area } &=\text { base } \times \text { height } \\\\ \text { Area } &=7 \times 4 \\\\ &=28 \end{aligned}4Write down your final answer with units squared.
In this case we are working with metres so our final answer must be in square metres.
\text { Area }=28 \mathrm{~m}^{2}Step-by-step guide: Area of a rectangle
See also: Area of a quadrilateral
Example 2: area of a triangle
Find the area of the triangle below.
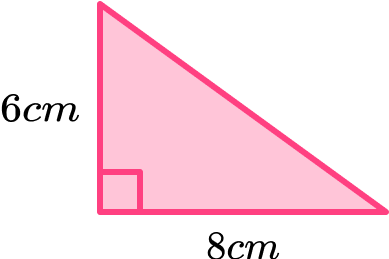
Write down the formula for the area of the shape.
Triangle,
A=\frac{1}{2} \times \text{base} \times \text{height} .
Identify the values required for the formula.
Base = 8cm
Height = 6cm
Substitute the values and calculate.
Write down your final answer with units squared.
In this case we are working with cm so our final answer must be in square cm.
\text { Area }=24 \mathrm{~cm}^{2}
Step-by-step guide: Area of a triangle
See also: Area of a right angled triangle
See also: Area of an isosceles triangle
See also: Area of an equilateral triangle
Example 3: area of a parallelogram
Find the area of the parallelogram below.

Write down the formula for the area of the shape.
Parallelogram,
\text { Area }=\text { base } \times \text { height } .
Identify the values required for the formula.
Base = 6cm
Perpendicular height = 30mm
We need all units to be the same to calculate the area. Here it is easiest to change 30mm to 3cm.
Height =3cm
Substitute the values and calculate.
Write down your final answer with units squared.
Step-by-step guide: Area of a parallelogram
See also: Area of a rhombus
Example 4: area of a trapezium
Find the area of the trapezium below.
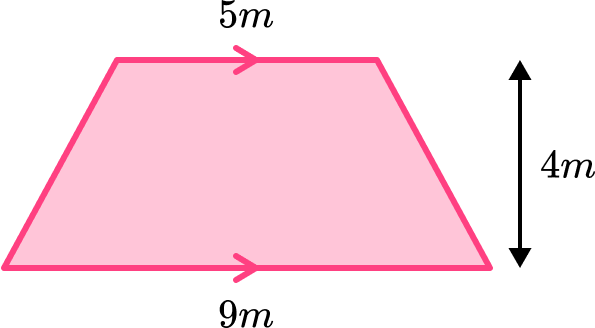
Write down the formula for the area of the shape.
Trapezium,
\text { Area }=\frac{1}{2}(a+b)h .
Identify the values required for the formula.
a and b are the parallel sides and h is the height of the trapezium.
a=5 and b=9
h=4
Substitute the values and calculate.
Write down your final answer with units squared.
Step-by-step guide: Area of a trapezium
Example 5: area of a circle
A circle has a diameter of 8mm.
Calculate its area. Give your answer to 1 decimal place.

Write down the formula for the area of the shape.
Circle,
\text{Area} = \pi r^{2} .
Identify the values required for the formula.
r is the radius of the circle. In this question we are given the diameter, 8mm. The radius is half of the diameter which is 4mm.
Radius = 4mm
Substitute the values and calculate.
Write down your final answer with units squared.
The question asks for the answer to be given to one decimal place so we need to round the answer.
\text { Area }=50.3 \mathrm{~mm}^{2}
Step-by-step guide: Area of a circle
See also: Pi r squared
Example 6: area of a compound shape
This shape is made from a square and a semicircle.
Find the area of the shape. Give your answer to 2 decimal places.
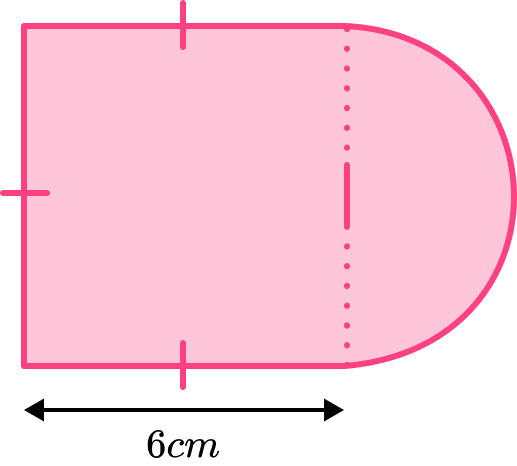
Write down the formula for the area of the shape.
Break down the compound shape into basic shapes.
The shape can be split into a square with side length 6cm and a semicircle with radius 3cm.
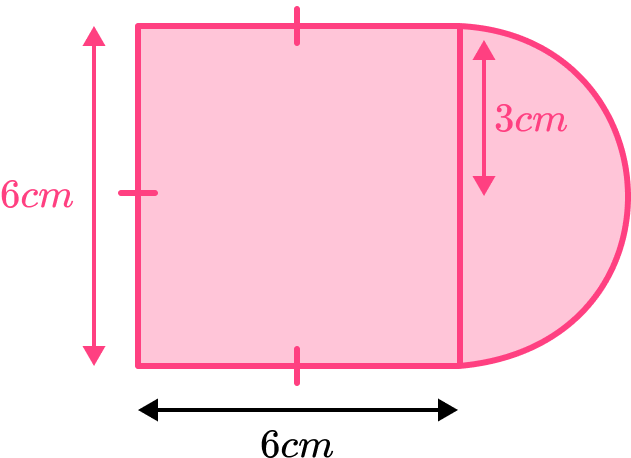
Square,
\text{Area of square} = \text{base} \times \text{height} .
Semi-circle,
\text{Area of a circle}=\pi r^{2} .
\text{Area of semi-circle }=\text{Area of circle } \div 2
Identify the values required for the formula.
Square,
Base =6cm, height =6cm .
Semi-circle,
Radius =3cm .
Substitute the values and calculate.
Square,
\text{Area of square} = \text{base} \times \text{height}
Base =6cm, height =6cm
\begin{aligned} \text{Area of square}&=6 \times 6\\\\ &=36 \mathrm{~cm}^{2} \end{aligned}
Semi-circle,
\text{Area of a circle}=\pi r^{2}
Radius =3cm
\begin{aligned} \text{Area of a circle }&=\pi \times 3^{2}\\\\ &=28.27433388 \end{aligned}
\begin{aligned} \text{Area of semi-circle }&=\text{Area of circle } \div 2\\\\ &=28.27433388 \div 2\\\\ &=14.13716694 \end{aligned}
Total Area =36+14.13716694=50.13716694
Write down your final answer with units squared.
Total area = 50.14cm^2
See also: Area of a hexagon
See also: Area of a pentagon
Example 7: using the area to find a length
The area of this triangle is 30cm^{2}. Work out the length of the side labelled x.

Write down the formula for the area of the shape.
Triangle,
A=\frac{1}{2} \times \text{base} \times \text{height} .
Identify the values required for the formula.
Area = 30cm^2
Height = 6cm
Substitute the values and calculate.
Write down your final answer with units squared.
In this case we are working with cm and square cm so our final answer must be in cm.
x=10cm
Example 8: using the area to find the radius
The area of this circle is 25 \pi m^{2}.
Work out the radius of the circle.

Write down the formula for the area of the shape.
Circle,
A=\pi r^{2} .
Identify the values required for the formula.
Substitute the values and calculate.
Write down your final answer with units squared.
Radius =5m
Common misconceptions
- Using an incorrect formula
There are several different formulae for the different shapes – make sure you use the correct one.
- Using the incorrect unit of area or not including units
Area calculations are measured in square units.
For example, square millimetres, square centimetres, square metres, square kilometres, square inches, square feet, square yards, square miles etc.
- Confusing perimeter, area and volume
Two dimensional shapes have a perimeter and an area. Three dimensional figures have a surface area and a volume. You need to make sure you are calculating the correct measurement required for each question.
- Calculating with different units
All measurements must be in the same units before calculating an area or surface area.
For example, you can’t have some measurements in cm and some in m.
- Using diameter instead of radius for a circle
To work out the area of a circle we need the radius, which is the distance from the centre of the circle to the edge of the circle.
Practice area questions
1. Find the area of the rectangle.





Use the formula
\text{Area }= \text{ base } \times \text{ height}
8 \times 3=24\mathrm{~cm}^{2}
2. Find the area of the triangle.





3. Find the area of the parallelogram in m^{2}.
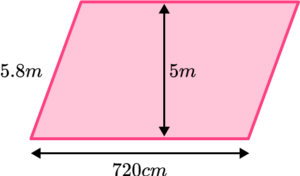




Convert 720cm into metres by dividing by 100.
\text{Base }=720 \div 100=7.2
\text{Area }= \text{ base } \times \text{ height}
Careful not to multiply by the length of the diagonal instead of the perpendicular height.
\begin{aligned} \text{Area }&=7.2 \times 5\\\\ &=36\mathrm{~m}^{2} \end{aligned}
4. Find the area of the trapezium below in cm^{2}.
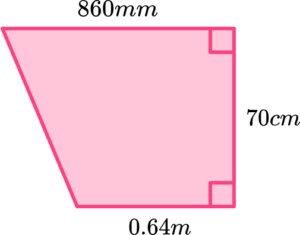




Convert 0.64m into 64cm and 860mm into 86cm.
\begin{aligned} \text{Area }&=\frac{1}{2}(a+b)h\\\\ &=\frac{1}{2} \times (64+86) \times 70\\\\ &=\frac{1}{2} \times 150 \times 70\\\\ &=5250 \mathrm{~cm}^{2} \end{aligned}
5. A circle has an area of 64 \pi \mathrm{~cm}^{2}.
What is the diameter of the circle?




6. Find the area of the shape.





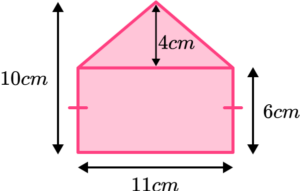
\begin{aligned} \text{Area of rectangle }&=\text{ base } \times \text{ height}\\\\ &=11 \times 6\\\\ &=66 \mathrm{~cm}^{2} \end{aligned}
\begin{aligned} \text{Area of triangle }&=\frac{1}{2} \times \text{ base } \times \text{ height }\\\\ &=\frac{1}{2} \times 11 \times 4\\\\ &=22 \mathrm{~cm}^{2} \end{aligned}
Total area: 66+22=88cm^2
Area GCSE questions
1. A square has a perimeter of 28cm. Find its area.
Circle your answer.
28cm^2 \quad \quad \quad 49cm^2 \quad \quad \quad 196cm^2 \quad \quad \quad 14cm^2
(2 marks)
Side length = 28\div 4 =7 \mathrm {~cm}
(1)
49cm^2(1)
2. These two shapes have the same area. Work out the height of the rectangle.
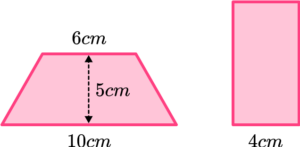
(3 marks)
Area of trapezium = \frac{1}{2} \times (6+10) \times 5 = 40 \mathrm{~cm}^{2}
(1)
Area of rectangle = 40cm^2
(1)
Height of rectangle = 40 \div 4 = 10 \mathrm{~cm}
(1)
3. Archie needs to paint a wall with two coats of paint.
The wall is pictured below with its measurements in metres.

A tin of paint covers 20m^{2}. How many tins of paint does Archie need for the two coats of paint?
(4 marks)
Splitting the shape into two or more shapes, e.g. a rectangle and triangle or a trapezium and rectangle.
(1)
Finding the area of one of the shape
(1)
Correct total area of 38.5m^2
(1)
Correct number of tins = 4
(1)
Learning checklist
You have now learned how to:
- Work out the area of triangles, quadrilaterals and circles
- Work out the area of compound shapes
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.