One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
Arithmetic Decimals Fractions BIDMAS Rounding numbers Converting metric units AnglesThis topic is relevant for:

2D Shapes
Here we will learn about 2D shapes, including symmetry, perimeter, area, circles, sectors, arcs and angles in polygons.
There are also 2D shapes worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What are 2D shapes?
2D shapes are flat shapes which only have two dimensions; length and width.
Some examples of common 2D shapes names are triangles, rectangles, pentagons, hexagons, heptagons, octagons, nonagons, decagons and circles.

We can solve problems involving 2D shapes using a variety of methods.
What are 2D shapes?

Polygons
Polygons are 2D shapes made from straight lines. You will deal with two different types of polygons.
Regular polygons
Regular polygons have specific properties. They have all sides of equal length and all interior angles are equal.
Examples of basic 2D shapes that are regular polygons are equilateral triangles and squares.
Irregular polygons
Irregular shapes (or polygons) do not have all equal sides and do not have all equal angles. When the number of sides is unknown, we describe this shape as an \textbf{n-gon} where the number of sides is given as \textbf{n}.
You will also need to be able to solve problems involving angles in polygons. The angles in a polygon can help determine whether a polygon is regular, a specific type of polygon or to determine how many sides a polygon has. You need to be familiar with interior and exterior angles of polygons.
Interior angles are angles that are contained within the polygon.

The sum of interior angles of any polygon can be calculated using the formula,
Sum of interior angles = (n-2) \times 180
where n represents the number of sides.
Exterior angles are supplementary to the interior angle. This means that the sum of the interior and exterior angles at a vertex always equals 180^{o}. We can use this property to find either the interior angle, or exterior angle at a vertex.
For any polygon the sum of exterior angles of a polygon 360^{o}.
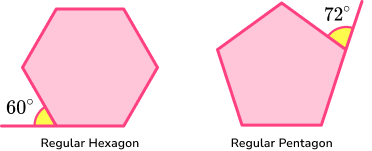
Step-by-step guide: Polygons
Symmetry
Symmetry is when a line is drawn through a shape to make one side of the line a reflection of the other. It is a property of a 2D polygon or 3D polyhedron.
There are two different types of symmetry that you need to be aware of. Lines of symmetry and rotational symmetry.
For example, a rectangle has two lines of symmetry

and has order 2 rotational symmetry.
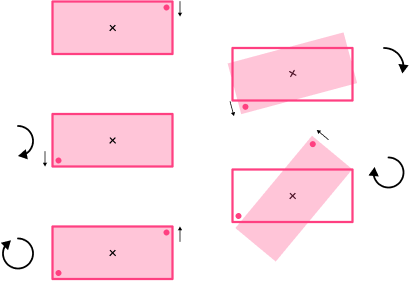
Step-by-step guide: Symmetry
Area
Area is a measure of how much space there is inside of a 2 dimensional shape.
Here are formulae we need to remember to calculate the area of certain 2D shapes.
These are seen in the table below.
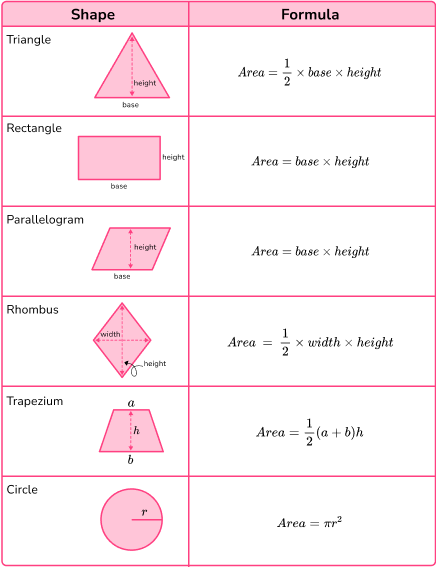
Step-by-step guide: How to work out area
Perimeter
The perimeter is the total distance around the outside of a 2D shape.
For example, let’s find the perimeter of the triangle.
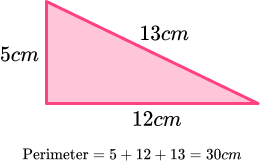
For example, let’s find the perimeter of the rectangle.
The opposite sides of a rectangle are equal, a and b are the side lengths.
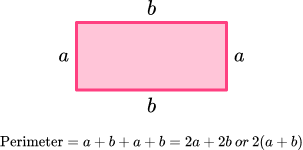
For example, let’s find the perimeter of the circle.
The perimeter of a circle is known as the circumference of a circle.
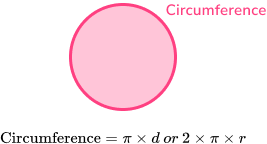
The circumference of this circle is
\begin{aligned} \text { Circumference } &=2 \times \pi \times r \\\\ &=2 \times \pi \times 12 \\\\ &=24 \pi \ \mathrm{ cm} \end{aligned}Step-by-step guide: How to work out perimeter
Circles, sectors and arcs
Circles are round plane figures whose boundaries consist of points equidistant from a fixed point (the centre of the circle).

As well as the area and circumference of a circle we can also work out the following.
Step-by-step guide: Circles, sectors and arcs
- Parts of a circle
The parts of a circle have specific names and properties which you need to know for all circle related questions. An important fact to remember is that the radius of a circle is half of its diameter.
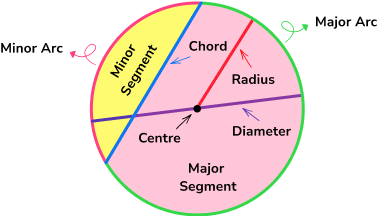
Step-by-step guide: Parts of a circle
- Area of a sector
The area of a sector is part of the area of a circle.
It can be found by using the formula \frac{\theta}{360} \times \pi r^{2}.
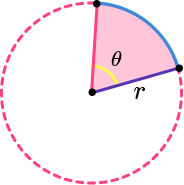
For example,
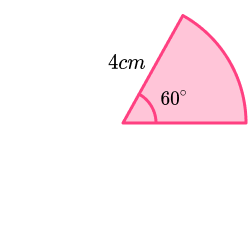
The area of this sector is
\begin{aligned} &=\frac{\theta}{360} \times \pi r^{2} \\\\ &=\frac{60}{360} \times \pi \times 4^{2} \\\\ &=\frac{1}{6} \pi \end{aligned}Step-by-step guide: Area of a sector
See also: Sector of a circle
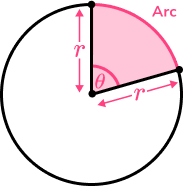
- Arc length
The arc of a circle is part of the circle’s circumference.
It’s length can be found using the formula \frac{\theta}{360} \times \pi d.
For example,
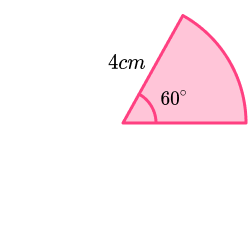
The arc length of this sector is
\begin{aligned} &=\frac{\theta}{360} \times \pi d \\\\ &=\frac{60}{360} \times \pi \times 8 \\\\ &=\frac{60}{360} \times \pi \times 8 \\\\ &=\frac{4}{3} \pi \end{aligned}Step-by-step guide: Arc length
See also: Arc of a circle
- Perimeter of a sector
To find the perimeter of a sector you need to find the arc length and then add it to the two straight sides which are both radii (i.e. the length around the outside of the sector).
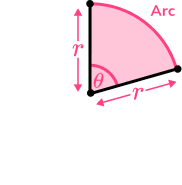
For example,
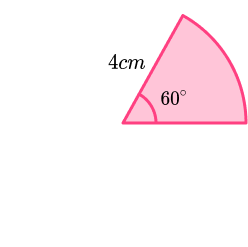
The perimeter of this sector is
\begin{aligned} &=\frac{60}{360} \times \pi \times 8+4+4 \\\\ &=\frac{4}{3} \pi+8 \end{aligned}Step-by-step guide: Perimeter of a sector
- Segment of a circle
A segment of a circle is created by an arc length and a chord.
You may have to find its area using a combination of mathematical rules such as trigonometry or Pythagoras’ theorem.
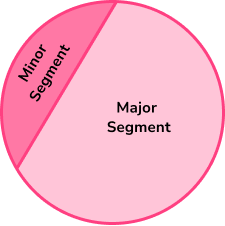
Step-by-step guide: Segment of a circle
- Equation of a circle
The equation of a circle (at GCSE) can be given in the form below
x^{2}+y^{2}=r^{2}.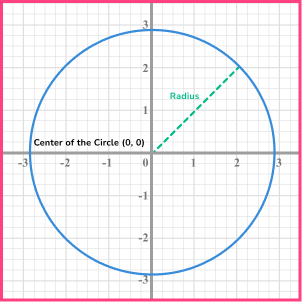
Step-by-step guide: Equation of a circle
How to use 2D shapes
We can use 2D shapes in lots of different ways.
We will learn about:
- Polygons
- Symmetry
- Area
- Perimeter
- Circles, sectors and arcs
Explain how to use 2D shapes

Area of 2D shapes worksheet

Get your free 2D shapes worksheet of 20+ area of 2D shapes questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Area of 2D shapes worksheet

Get your free 2D shapes worksheet of 20+ area of 2D shapes questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE2D shapes examples
Example 1: regular / irregular polygons
The shape ABCDE below is made from two scalene triangles, and one isosceles triangle. M is a midpoint on the line CD. AM is a line of symmetry.
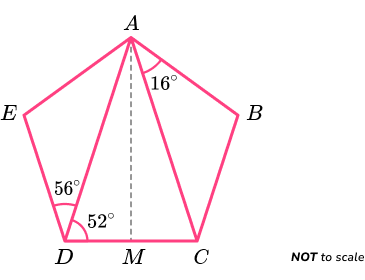
Determine what type of polygon ABCDE is and determine if it is regular or irregular.
- State / calculate the number of sides of the polygon.
The polygon ABCDE has 5 sides so it is a type of pentagon.
2Determine the size of the angles / side lengths within the polygon.
As triangle ACD is isosceles and AM is a line of symmetry, angle ACD = angle ADC = 52^{o}.
As the sum of angles in a triangle is 180^{o},
angle CAD = 180-(52+52)=76^{o}.
As AM is a line of symmetry, triangles ABC and ACD must be congruent, sharing the same angles and side lengths. This means that,
- Angle BCA = angle ADE =56^{o}
- Angle DAE = angle CAB =16^{o}
Again, as the sum of angles in a triangle total 180^{o},
angle AED = 180-(56+16)=108^{o}.
This is the same for angle ABC as it is symmetrical to angle AED and therefore equal.
We now have all of the following angles,
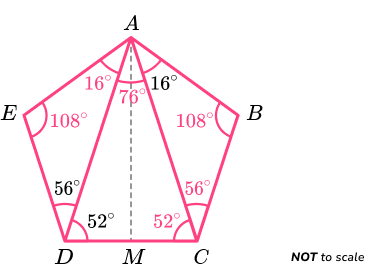
3Recognise the other properties of the polygon.
For a pentagon to be regular, all of the interior angles must be the same and side lengths must be the same.
Furthermore, as the interior angle sum of a pentagon is 540^{o}, each interior angle of a regular pentagon is equal to
540\div{5}=108^{o}.Adding the angles at each vertex together, we have
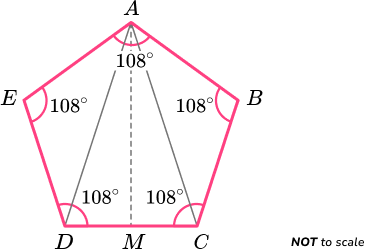
Each interior angle of the polygon ABCDE is equal to 108^{o}.
However, the triangles AED and ABC are scalene. Therefore, AB has a different length to BC .
The interior angles are equal but the side lengths are not equal.
The polygon is an irregular pentagon.
Example 2: types of quadrilateral
Determine what type of quadrilateral ABCD is below.
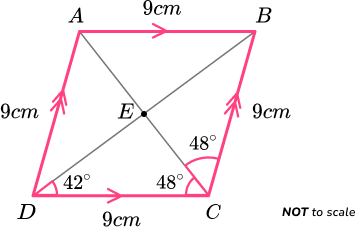
Determine the size of the angles / side lengths within the quadrilateral.
All four side lengths are equal to 9cm with two pairs of parallel sides.
Angle BCD = 48+48=96^o and so ABCD cannot be a square.
CDE is a triangle. As the sum of angles in a triangle total 180^{o},
angle CED = 180-(42+48)=90^{o}.
Labelling this on the diagram, we have
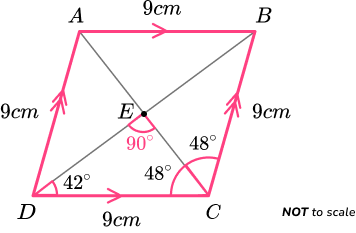
Recognise the other properties of the polygon.
As vertically opposite angles are equal, angle AED = angle CED = 90^{o}.
As the sum of angles on a straight line total 180^{o},
Angle AED = 180-90=90^{o}.
This is also true for angle BEC.
We therefore have the diagonals intersecting at 90 degrees.
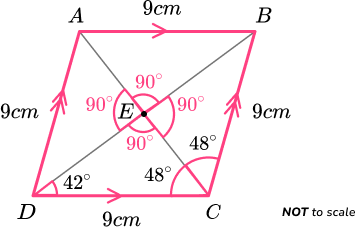
ABCD is a rhombus.
Remember: The properties of a rhombus are,
- Four equal sides
- Opposing sides are parallel
- Two opposing pairs of equal angles
- Diagonals bisect each other at 90 degrees
- Two lines of symmetry
- Rotational symmetry of order 2
Example 3: symmetry
State the number of lines of symmetry for a regular hexagon.
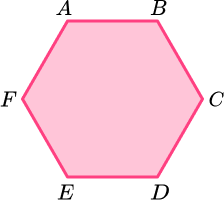
Locate the centre of the 2D shape.
To locate the centre of a shape with an even number of vertices, draw a pair of straight lines connecting two opposing vertices.
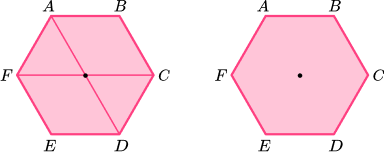
Use a ruler to visualise a horizontal and/or vertical line of symmetry through the centre of the shape.
The regular hexagon has a vertical line of symmetry.
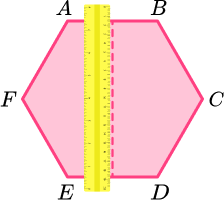
The regular hexagon has a horizontal line of symmetry.

Continue to rotate the ruler around 180 degrees over the centre point to cover all sides and vertices.
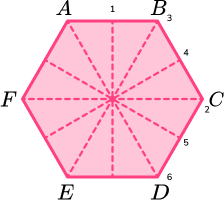
Line of symmetry 3.

Line of symmetry 4.

Line of symmetry 5.

Line of symmetry 6.

A regular hexagon has 6 lines of symmetry.
Example 4: area of an isosceles triangle
Calculate the area of the triangle below.
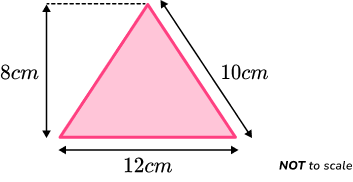
Identify the base and perpendicular height of the triangle.
The two values that are perpendicular to one another are the 12cm along the base, and the vertical height of 8cm.
The 10cm is not required to find the area of this triangle.
Write the area formula.
The area of a triangle formula is,
\text{Area of a triangle}=\cfrac{\text{base }\times\text{height}}{2}.
Substitute known values into the area formula.
As the base = 12cm and the height = 8cm, we have
\text{Area of a triangle }=\cfrac{12\times{8}}{2}.
Solve the equation.
Write the answer, including the units.
As the units of length are in centimetres, the units of area are square centimetres.
The area of the triangle is 48cm^{2}.
Example 5: circumference of a circle
Calculate the circumference of a circle with a radius of 4cm. Write your answer correct to 2 decimal places.

Find the radius or diameter of the circle.
The radius of the circle is 4cm.
Use the relevant formula to calculate the circumference of the circle.
The formula for the circumference of a circle (C) in terms of the radius (r) is
C=2\pi{r}.
Substituting r=4 into the formula, we have
\begin{aligned}
C&=2\times\pi\times{4} \\\\
&=8\times\pi \\\\
&=8\pi \\\\
&=25.13274123 \\\\
&=25.13\text{ (2dp)}
\end{aligned}
Give your answer clearly with the correct units.
The circumference of the circle is 25.13cm \ (2dp).
Example 6: perimeter of compound shapes – real life problem
A car park needs a new boundary fence installing. A sketch of the car park is given below.
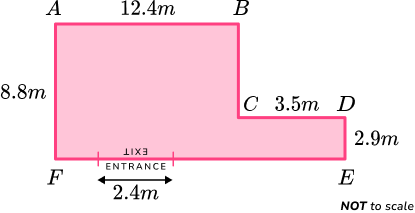
Determine the length of the boundary wall (the car park entrance/exit must not be included in this value).
Add all the side lengths.
A few of the side lengths are missing and so we need to calculate these lengths first.
As AF = 8.8m and DE = 2.9m, the length of BC can be calculated by subtracting DE from AF,
8.8-2.9 = 5.9m.
As AB = 12.4m and CD = 3.5m, the length of EF can be calculated by adding AB and CD together,
12.4+3.5=15.9m.
Writing these two measurements onto the diagram, we have

The perimeter is the sum of the side lengths and so we have the sum,
12.4+5.9+3.5+2.9+15.9+8.8=49.4m.
Note: For an L shape, this is the same as doubling the sum of the height and the width ((8.8+15.9)\times{2}=49.4m).
Write the final answer with the correct units.
As we need to calculate the boundary excluding the entrance/exit, we need to subtract the width of the entrance from the total perimeter.
49.4-2.4=47m
The perimeter of the car park excluding the entrance/exit is 47m.
Example 7: area of a sector
A circular cake is cut into 8 equal slices as shown below.
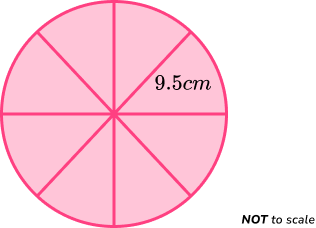
Calculate the area of the top of one slice of cake.
Find the length of the radius \textbf{r} .
The radius r = 9.5cm.
Find the size of the angle creating the sector
The angle of the sector is one eighth of a full turn. As a full turn is 360 degrees,
360\div{8}=45.
The angle of the sector is 45^{o}.
Substitute the value of the radius and the angle into the formula for the area of a sector.
The formula for the area of the sector is
\text{Area of a sector }=\frac{\theta}{360}\times\pi{r}^{2}
where \theta is the angle of the sector, and r is the radius of the overall circle.
Substituting \theta=45^{o} and r = 9.5cm, we have
\begin{aligned} \text{Area of a sector }&=\frac{45}{360}\times\pi\times{9.5}^{2} \\\\ &=\frac{1}{8}\times\pi\times{90.25} \\\\ &=11.28125\pi \\\\ &=35.44109212 \\\\ &=35.44\text{cm}^{2}\text{ (2dp)} \end{aligned}
Clearly state your answer.
The area of the top of the cake slice is 35.44cm^{2}.
Example 8: equation of a circle
Determine the equation of the unit circle, centred at the origin.
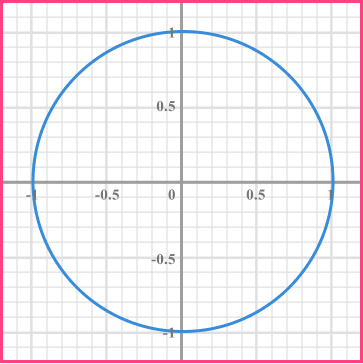
Write the general equation of a circle.
The general equation of a circle is x^{2}+y^{2}=r^{2}.
State any variables you know.
The radius of the unit circle is 1. We can also see this as the centre of the circle lies at the point (0,0) and a coordinate on the circumference of the circle is (1,0), giving us a radius of 1.
Substitute any values you know into the equation.
Substituting r=1 into the equation of a circle, we have
x^{2}+y^{2}=1^{2}.
Use the information you have to solve the problem.
Evaluating 1^{2} we get 1^{2}=1 \times 1=1.
Clearly state the answer.
The equation of the unit circle, centred at the origin is x^{2}+y^{2}=1.
Common misconceptions
- Rotational symmetry/lines of symmetry
Lines of symmetry are often confused with rotational symmetry. A line of symmetry on a two-dimensional shape divides the shape equally into two symmetrical pieces.
Rotational symmetry is the number of times a shape fits into itself when rotated around its centre.
- Confusing perimeter with area
Remember, perimeter is distance around the outside of a shape, whilst area is the space inside the shape.
- Angles properties
Ensure you have a good understanding of the different types of angles (for example, acute angles and right angles) along with how to calculate angles in polygons and angles in parallel lines.
Getting these confused can lead to misconceptions when problem solving.
Practice 2D shapes questions
1. Which of the following shapes has 2 lines of symmetry and rotational symmetry order 2.
Parallelogram

Rhombus

Square

Kite

A parallelogram has no lines of symmetry and rotational symmetry order 2.
A square has 4 lines of symmetry and rotational symmetry order 4.
A kite has 1 line of symmetry and no rotational symmetry.

2. The rectangle has a perimeter of 42cm. Find x.
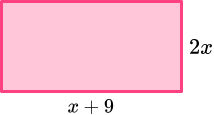




Form an equation for the perimeter.
2x+x+9+2x+x+9=18
6x+18=42
Solve the equation, to find x=4.
3. Find the area of the isosceles triangle.
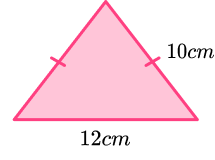




This is an isosceles triangle. We can split it vertically to form two identical triangles with base 6cm, and hypotenuse 10cm.
We then use Pythagoras’ theorem to find the height of the triangle.
\begin{aligned} &a^{2}+b^{2}=c^{2} \\\\ &6^{2}+\text { height }{ }^{2}=10^{2} \\\\ &\text { height }{ }^{2}=100-36 \\\\ &\text { height }{ }^{2}=64 \\\\ &\text { height }=8cm \end{aligned}
Then we can use the formulae for the area of a triangle, and multiply the height by the base (remembering to use the base as 12cm for the area of the whole triangle) then divide by 2.
\begin{aligned} \text { Area of a triangle } &=\frac{1}{2} \times \text { base } \times \text { height } \\\\ &=\frac{1}{2} \times 12 \times 8 \\\\ &=48cm^{2} \end{aligned}
4. The sector has an area of \frac{27}{2} \pi cm^2, Find the perimeter in terms of \pi.
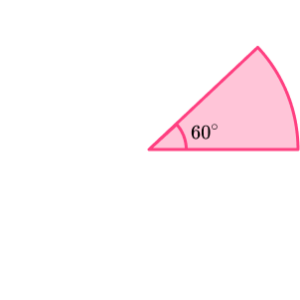




To find the perimeter of the sector we need to calculate the arc length. To do this we need to know the diameter of the sector.
We can work backwards using the formula for the area of a sector to find the radius to help us find the diameter.
\text { Area of a sector }=\frac{\theta}{360} \times \pi \times r^{2}
Substituting in what we know,
\begin{aligned} &\frac{60}{360} \times \pi \times r^{2}=\frac{27}{2} \pi \\\\ &\frac{60}{360} r^{2}=\frac{27}{2} \\\\ &r^{2}=81 \\\\ &r=9cm \end{aligned}
Now we can calculate the arc length. If the radius is 9cm, the diameter must be 18cm.
\text { Arc length }=\frac{\theta}{360} \times \pi \times d
Substituting in what we know,
\begin{aligned} &=\frac{60}{360} \times \pi \times 18 \\\\ &=3 \pi \ cm \end{aligned}
For the total perimeter we need to add the two radii to the arc length.
\text { Perimeter }=3 \pi+18cm
5. What is the sum of the interior angles of a pentagon?




6. A regular polygon has an interior angle of 165^{\circ}. How many sides does it have?




The interior and exterior angle of a polygon sum to 180^{\circ}. We can find the exterior angle using this fact.
\begin{aligned} &\text{Exterior angle }=180-\text{interior angle} \\\\ &\text{Exterior angle }=180-165=15^{\circ} \end{aligned}
To find out the number of sides we then do,
\text { Number of sides }=360 \div 15=24.
2D shapes GCSE questions
1. The hexagon ABCDEF has one line of symmetry.
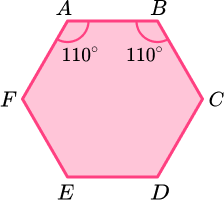
Angle FAB = angle ABC = 110^{\circ}.
Angle AFE = angle BCD.
Angle FED = angle CDE.
Angle CDE : angle BCD = 3 : 2.
Find the size of angle AFE .
(5 marks)
Indicating sum of angles is 720^{\circ} or 540^{\circ} if line of symmetry used to form a pentagon.
(1)
Finding the sum of AFE and FED is 250^{\circ}.
(1)
Use of ratio 3:2 or sight of 3x and 2x.
(1)
Finding x=50.
(1)
Angle AFE = 100^{\circ}.
(1)
2. The perimeter of the rectangle is twice the perimeter of the isosceles triangle.
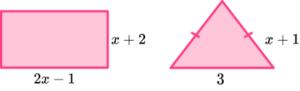
Find the area of the rectangle.
(5 marks)
Correct expression for perimeter of rectangle or triangle,
6x+2 \ , \ 2x+5.(1)
Forming an equation linking the perimeters.
For example, 6x+2=2(2x+5) or equivalent.
(1)
Solving equation to get x=4.
(1)
Correctly substituted into length and width of rectangle.
(1)
Area given as 42cm^{2}.
(1)
3. The sector has a perimeter 25cm and radius 6cm.
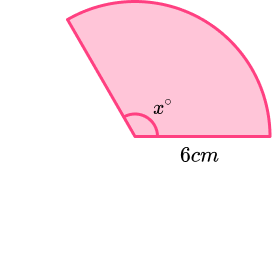
Find the size of angle x. Give your answer to 3 significant figures.
(3 marks)
Sight of arc length given as 13cm.
(1)
Process to use formula \frac{x}{360} \times 2 \times \pi \times 6=13
(1)
x=124^{\circ}(1)
Learning checklist
You have now learned how to:
- Identify lines of symmetry and order of rotational symmetry in 2D shapes
- How to work out the perimeter
- Work out the area of triangles, quadrilaterals and circles
- Work out the area of compound shapes
- Identify and apply circle definitions and properties
- Calculate the circumference of a circle
- Calculate the area and arc length of a sector
- Distinguish between regular and irregular polygon
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.