Equation of a circle

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

Coordinates maths How to find the midpoint Parts of a circle Equations Quadratic equations Expanding brackets Solving equations Surds Substitution

This topic is relevant for:

GCSE Maths Geometry and Measure 2D Shapes CSA

Equation Of A Circle

Here we will learn about the equation of a circle including how to recognise the equation of a circle, form an equation of a circle given its radius and centre, use the equation of a circle to find its centre and radius, and solve problems.

There are also equation of a circle worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is the equation of a circle?

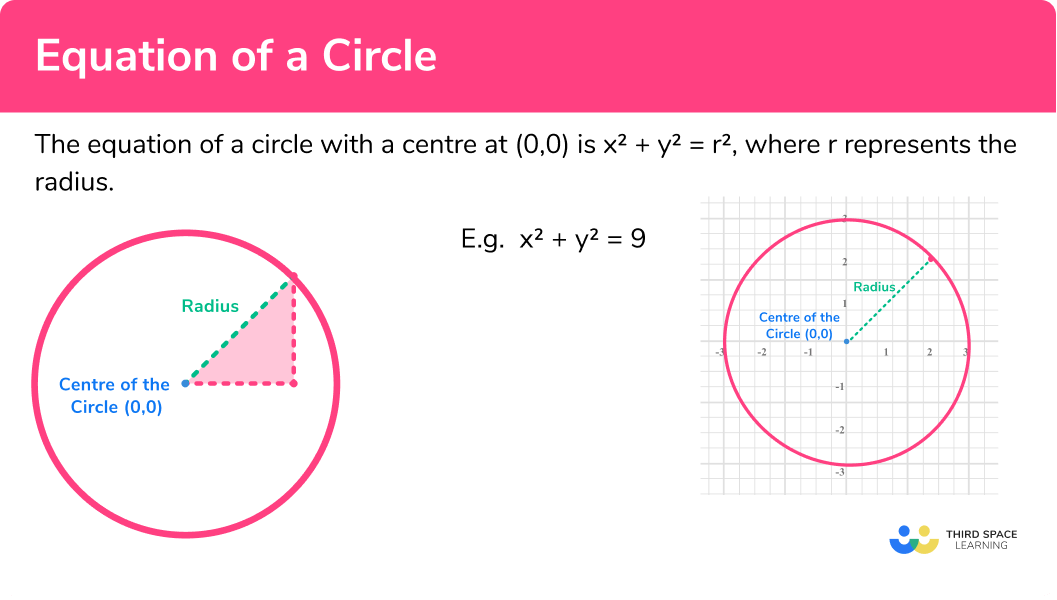
The equation of a circle is $x^2 + y^2 = r^2$ , where r represents the radius (with a centre at $0,0$ ).

The definition of a circle is a set of all points on a plane that are a fixed distance from a centre. That distance is called the radius.

For GCSE, you need to be able to recognise and use the equation of a circle with centre at the origin so consider the drawing below of a circle on a set of axes:

Now consider a right angled triangle created when the radius of the circle is the hypotenuse of the triangle (see the below figures):

The horizontal line is the distance to the $x$ coordinate.
The vertical line is the distance to the $y$ coordinate.
The hypotenuse is the distance of the radius.

You can now apply Pythagoras’ theorem to the above:

$a^2+b^2=c^2$

$a$ = $x$ coordinate

$b$ = $y$ coordinate

$c$ = radius

Therefore the general form of the equation of a circle centred at $(0,0)$ is:

$x^2+y^2=r^2$

E.g.

Draw circle with equation $x^2+y^2=9$

The circle has a centre at $(0,0)$ .

$9$ represents $r^2$ , so the radius $r$ is given by $3$ .

What is the equation of a circle?

How to use the equation of a circle

In order to solve problems involving the equation of a circle:

Write the general equation of a circle.
State any variables you know.
Substitute any values you know into the equation.
Use the information you have to solve the problem.
Clearly state the answer.

How to use the equation of a circle

Equation of a circle worksheet

Get your free equation of a circle worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD NOW

Equation of a circle worksheet

Get your free equation of a circle worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD NOW

Equation of a circle is part of our series of lessons to support revision on circles, sectors and arcs. You may find it helpful to start with the main circles, sectors and arcs lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Equation of a circle examples

Example 1: writing the equation of a circle with a centre at the origin

What is the equation of a circle with a radius of $3$ and a centre at the origin

Write the general equation of a circle.

x^2+y^2=r^2

2State any variables you know.

Radius = $3$

3Substitute any values you know into the equation.

x^2+y^2=3^2

4Use the information you have to solve the problem.

\[\begin{aligned} &x^{2}+y^{2}=3^{2} \quad \quad \quad \text{Simplify the equation by squaring the radius} \\ &x^{2}+y^{2}=9 \end{aligned}\]

5Clearly state the answer.

Equation of the circle is :

x^2+y^2=9

Example 2: writing the equation of a circle with a centre at the origin

What is the equation of a circle with a radius of $1.5$ and a centre at the origin.

Write the general equation of a circle.

x^2+y^2=r^2

State any variables you know.

Radius = $1.5$

Substitute any values you know into the equation.

x^2+y^2=1.5^2

Use the information you have to solve the problem.

\[\begin{aligned} &x^{2}+y^{2}=1.5^{2} \quad \quad \quad \text {Simplify the equation by squaring the radius} \\ &x^{2}+y^{2}=2.25 \end{aligned}\]

Clearly state the answer.

Equation of the circle is:

x^2+y^2=2.25

Example 3: writing the equation of a circle with a centre at the origin

What is the equation of a circle with a radius of $\sqrt5$ and a centre at the origin.

Write the general equation of a circle.

x^2+y^2=r^2

State any variables you know.

Radius = $\sqrt5$

Substitute any values you know into the equation.

x^2+y^2=\sqrt5^2

Use the information you have to solve the problem.

\[\begin{aligned} &x^{2}+y^{2}=(\sqrt{5})^{2} \quad \quad \quad \text {Simplify the equation by squaring the radius } \\ &x^{2}+y^{2}=5 \end{aligned}\]

Clearly state the answer.

Equation of the circle is:

x^2+y^2=5

Example 4: finding the radius of a circle given its equation

What is the radius of the circle with the equation

x^2+y^2=4

Write the general equation of a circle.

x^2+y^2=r^2

State any variables you know.

Radius is unknown

Equation of the circle is given as $x^2+y^2=4$

Substitute any values you know into the equation.

We do not know any variables so we are unable to substitute here.

Use the information you have to solve the problem.

We that the radius squared is equal to $4$ , so

\[\begin{aligned} r^{2}&=4 \\ r&=\sqrt{4} \\ r&=2 \quad \text {You only use the positive value as radius is measure of distance} \end{aligned}\]

Clearly state the answer.

The radius is $2.$

Example 5: finding the radius of a circle given its equation

What is the radius of the circle with the equation

x^2+y^2=15

Give you answer to $2$ decimal places.

Write the general equation of a circle.

x^2+y^2=r^2

State any variables you know.

Radius is unknown. Equation of the circle is given as $x^2+y^2=15$

Substitute any values you know into the equation.

We do not know any variables so we are unable to substitute here.

Use the information you have to solve the problem required.

We know the equation of the circle is given in the question, therefore, we can create an equation for the radius:

\[\begin{aligned} r^{2}&=15 \\ r&=\sqrt{15} \\ r&=3.87298 \quad \text {You only use the positive value as radius is measure of distance} \end{aligned}\]

Clearly state the answer.

The question asks for the answer to be given to $2$ decimal places, therefore: $r = 3.87$

Example 6: finding the radius of a circle given its equation

What is the radius of the following circle?

2x^2+2y^2=100

Give your answer to $1$ decimal place.

Write the general equation of a circle.

x^2+y^2=r^2

State any variables you know.

Radius is unknown. Equation of the circle is given as $2x^2+2y^2=100$

Substitute any values you know into the equation.

We do not know any variables so we are unable to substitute here.

Use the information you have to solve the problem required.

We need to rearrange the equation so it is in the form:

x^2+y^2=r^2

Therefore,

\[\begin{aligned} 2 x^{2}+2 y^{2}&=100 \quad \quad \quad \text { Divide all terms by 2 } \\ x^{2}+y^{2}&=50 \end{aligned}\]

And so:

\[\begin{aligned} &r^{2}=50 \\ &r=\sqrt{50} \\ &r=7.071 \quad \end{aligned}\]

Clearly state the answer.

The question asks for the answer to be given to $1$ decimal places, therefore: $r=7.1$

Common misconceptions

The radius squared

Remember in the equation the radius is shown as a squared value. To find the radius you need to square root this value.

The radius and negatives

The radius cannot be negative because as the radius is a length it must always be a positive value.

Equation in correct form

Remember in order to apply the equation of a circle to a question it must be in the form: $x^2+y^2=r^2$

Practice equation of a circle questions

x^2+y^2=16

x^2+y^2=4

x^2+y^2=2

16

\begin{aligned} x^2+y^2=r^2\\ x^2+y^2=4^2\\ x^2+y^2=16 \end{aligned}

36

x^2+y^2=6

x^2+y^2=12

x^2+y^2=36

\begin{aligned} x^2+y^2=r^2\\ x^2+y^2=6^2\\ x^2+y^2=36 \end{aligned}

x^2+y^2=1.73

x^2+y^2=3

3

x^2+y^2=9

\begin{aligned} x^2+y^2=r^2\\ x^2+y^2=\sqrt3^2\\ x^2+y^2=3 \end{aligned}

10000

10

100

x^2+y^2=10

\begin{aligned} r^{2}=100\\ r=\sqrt{100}\\ r=10 \end{aligned}

20

4.47

400

x^2+y^2=10

\begin{aligned} r^{2}=20 \\ r=\sqrt{20} \\ r=4.47 \end{aligned}

64

16

4

2

\begin{aligned} 4x^2+4y^2=64\\ x^{2}+y^{2}=16 \end{aligned}

Therefore,

\begin{aligned} r^{2}=16 \\ r=\sqrt{16} \\ r=4 \end{aligned}

Equation of a circle GCSE questions

1. What is the equation of the circle with centre $(0, 0)$ and radius of $2\sqrt3$ units?

(2 marks)

Show answer

$2\sqrt3$ being squared at any point, or $12$ seen

(1)

$x^2+y^2=12$

(1)

2. What is the equation of the circle with centre $(0, 0)$ and radius of $\frac{2}{3}$ units?

(2 marks)

Show answer

$\frac{2}{3}$ being squared at any point, or $\frac{4}{9}$ oe seen

(1)

$x^2+y^2=\frac{4}{9}$ oe

(1)

3. Find the radius of the circle with the following equation.

Give your answer in the form $a\sqrt b$

(3 marks)

Show answer

Divide equation by $5$ or $x^2+y^2=40$ seen

(1)

$\sqrt40$

(1)

$2\sqrt10$

(1)

Learning checklist

You have now learned how to:

Identify and apply circle definitions and properties, including: centre, radius, chord, diameter, circumference

Recognise and use the general equation of a circle with centre at the origin

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.