One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

Parts of a circle Area of a sector Area of a triangle Arc length Pythagoras’ theorem Cosine rule Area of a triangle (1/2 abSinC) Rounding

This topic is relevant for:

GCSE Maths Geometry and Measure 2D Shapes CSA

Segment of a Circle

Segment Of A Circle

Here we will learn about the segment of a circle including how to identify the segment of a circle and how to find the area of a segment given the different parts of a circle.

There are also parts of a circle worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is the segment of a circle?

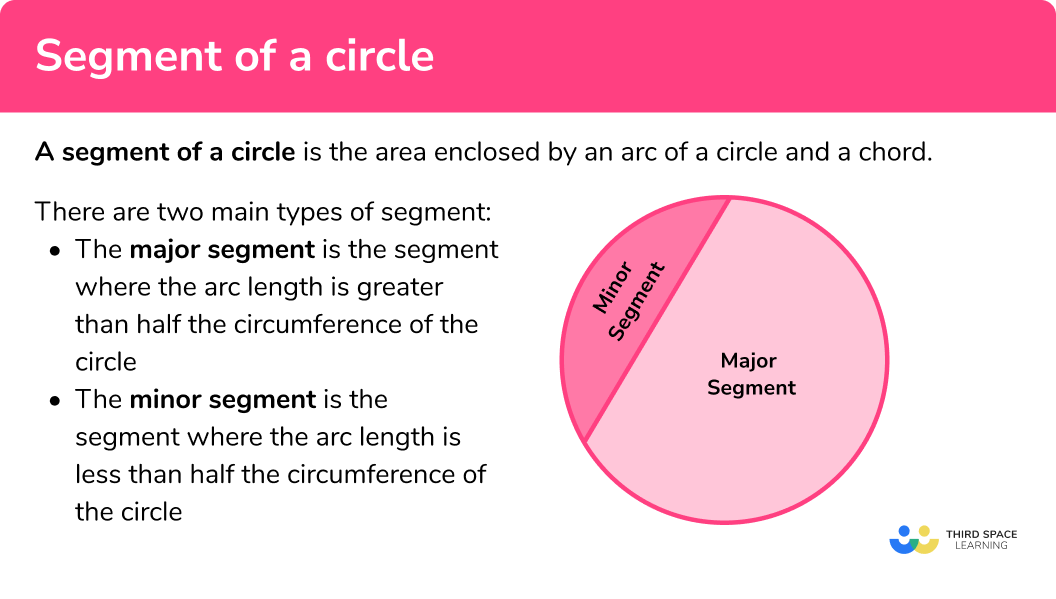
A segment of a circle is the area enclosed by an arc of a circle and a chord.

There are two main types of segment:

The major segment is the segment where the arc length is greater than half the circumference of the circle
The minor segment is the segment where the arc length is less than half the circumference of the circle

An arc is a fraction of the circumference of a circle.

A chord is a line segment that connects two points of a circle.

A segment where the chord passes through the centre of the circle is called a semicircle.

What is the segment of a circle?

How to solve problems involving a segment of a circle

In order to solve problems involving a segment of a circle:

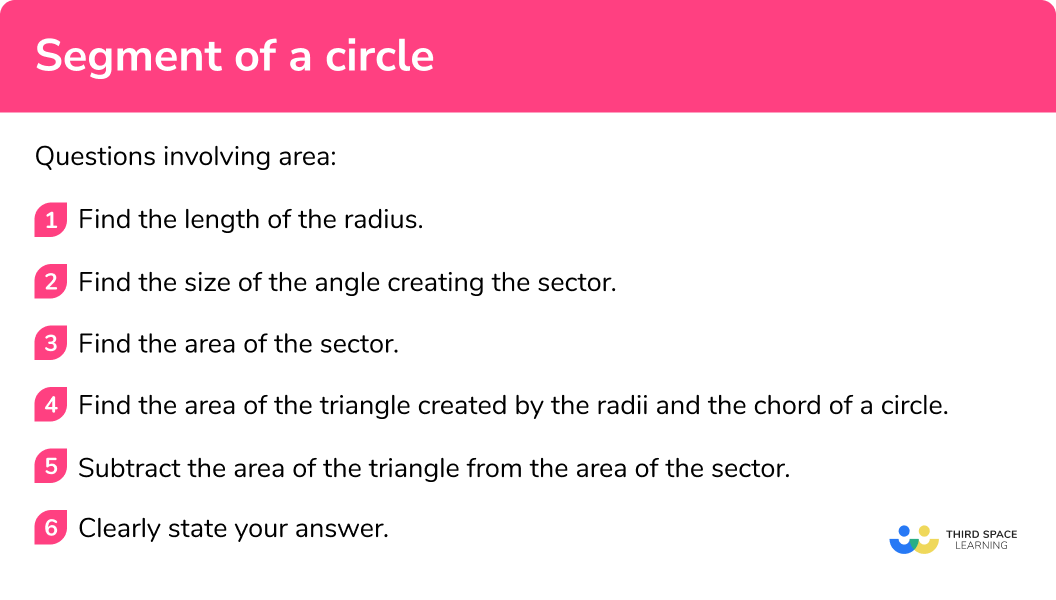
Questions involving area

Find the length of the radius.
Find the size of the angle creating the sector.
Find the area of the sector.
Find the area of the triangle created by the radii and the chord of a circle.
Subtract the area of the triangle from the area of the sector.
Clearly state your answer.

How to solve problems involving a segment of a circle (area)

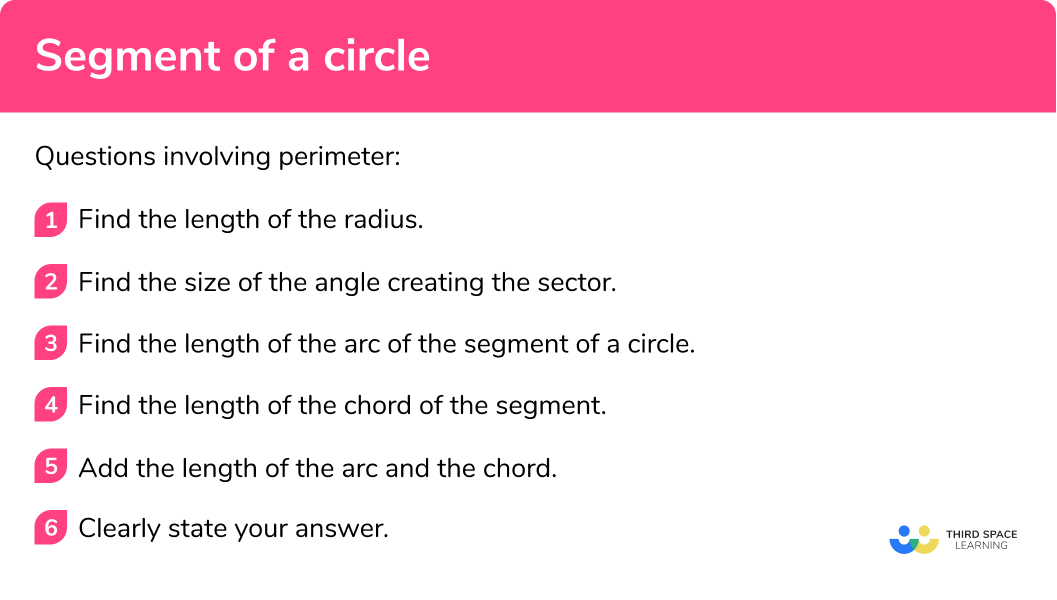
Questions involving perimeter

Find the length of the radius.
Find the size of the angle creating the sector.
Find the length of the arc of the segment of a circle.
Find the length of the chord of the segment.
Add the length of the arc and the chord.
Clearly state your answer.

How to solve problems involving a segment of a circle (perimeter)

Segment and other parts of a circle worksheet

Get your free parts of a circle worksheet of 20+ questions and answers on all parts of circles including segments. With reasoning and applied questions.

DOWNLOAD FREE

Segment and other parts of a circle worksheet

Get your free parts of a circle worksheet of 20+ questions and answers on all parts of circles including segments. With reasoning and applied questions.

DOWNLOAD FREE

Segment of a circle is part of our series of lessons to support revision on circles, sectors and arcs. You may find it helpful to start with the main circles, sectors and arcs lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Segment of a circle examples

Example 1: calculate the area of a segment of a circle

Calculate the area of the segment shown below. Give your answer to $3$ significant figures

Find the length of the radius.

Length of the radius of the circle: $7cm$

2Find the size of the angle creating the sector.

The size of the angle creating the sector (made by the two radii) is $90^{\circ}$ .

3Find the area of the sector.

\[\text{Area of sector }=\frac{\theta}{360} \times \pi r^{2}\\ =\frac{90}{360} \times \pi \times 7^{2} \\ =\frac{49}{4} \pi\]

Area of sector: $\frac{49}{4} \pi \mathrm{cm}^{2}$

It is important to not round the answer at this stage of the question

4Find the area of the triangle created by the radii and the chord.

\[\text{Area of triangle} = \frac{1}{2} a b \sin C \\ =\frac{1}{2} \times 7 \times 7 \times \sin(90)\\ =24.5\]

Area of triangle: $24.5cm^{2}$

5Subtract the area of the triangle from the area of the sector.

\[\text{Area of sector – Area of triangle} = \frac{49}{4} \pi-24.5\\ =13.9845…\]

6Clearly state your answer.

The question asked you to round your answer to $3$ significant figures

Area of the segment of the circle= $13.9845...cm^{2}=14.0cm^{2}$ ( $3$ .s.f.)

Example 2: calculate the perimeter of a segment

Calculate the perimeter of the segment shown below. Give your answer to $3$ decimal places

Find the length of the radius.

Length of radius: $7cm$

Find the size of the angle creating the sector.

The size of the angle creating the sector (made by the two radii) is $90^{\circ}$

Find the length of the arc of the segment.

\[\text{Arc length}=\frac{\theta}{360} \times 2 \pi r \\ =\frac{90}{360} \times 2 \pi \times 7 \\ =\frac{7}{2} \pi\]

Length of the arc: $\frac{7}{2} \pi cm$

Find the length of the chord of the segment.

In this question you can see the two radii and the chord form a right angled triangle. This means you can use Pythagoras’ theorem to find the length of the chord, which is the hypotenuse of the triangle.

\[a^{2}+b^{2}=c^{2} \\ 7^{2}+7^{2}=c^{2} \\ 49+49=c^{2} \\ 98=c^{2} \\ 7 \sqrt{2}=c \quad \quad \quad \text{square root both sides of the equation}\]

Therefore the length of the chord is $7 \sqrt{2} \mathrm{cm}$

Add the length of the arc and the chord.

\[\text{Length of the arc }+\text{ Length of the chord } = \frac{7}{2} \pi+7 \sqrt{2}\\ =20.895069…\]

Clearly state your answer.

The question asked you to round your answer to $3$ decimal places

Perimeter of segment: $20.895069\dotscm= 20.895cm (3.d.p)$

Example 3: calculate the area of a segment given the length of the radii and the angle

Calculate the area of the segment shown below. Give your answer to $3$ decimal places

Find the length of the radius.

Length of radius: $5cm$

Find the size of the angle creating the sector.

The size of the angle creating the sector (made by the two radii) is $100^{\circ}$ . This is given in the question.

Find the area of the sector.

\[\text{Area of sector}=\frac{\theta}{360} \times \pi r^{2}\\ =\frac{100}{360} \times \pi \times 5^{2} \\ =\frac{125}{18} \pi\]

Area of sector: $\frac{125}{18} \pi \mathrm{cm}^{2}$

Find the area of the triangle created by the radii and the chord.

\[\text{Area of triangle }=\frac{1}{2} a b \sin C \\ =\frac{1}{2} \times 5\times 5 \times \sin(100)\\ =12.3100…\]

Area of triangle: $12.3100…cm^{2}$

Subtract the area of the triangle from the area of the sector.

\[\text{Area of sector} – \text{Area of triangle } =\frac{125}{18} \pi\\ =9.50661565…\]

Clearly state your answer.

The question asked you to round your answer to $3$ decimal places

Area of segment: $9.50661565...cm^{2}= 9.507cm^{2} (3.d.p)$

Example 4: calculate the perimeter of a segment given the length of the radii and the angle

Calculate the perimeter of the segment shown below. Give your answer to $3$ decimal places.

Find the length of the radius.

Length of radius: $9cm$

Find the size of the angle creating the sector.

Size of angle: $80^{\circ}$

Find the length of the arc of the segment of a circle.

\[\text{Arc length}=\frac{\theta}{360} \times 2 \pi r \\ =\frac{80}{360} \times 2 \pi \times 9 \\ =4 \pi\]

Length of the arc: $4 \pi cm$

Find the length of the chord of the segment.

In this question, the triangle is not a right angled triangle so we cannot use Pythagoras’ Theorem to find the missing length. Instead we can use the cosine rule.

Length of chord:

\[a^{2}=b^{2} + c^{2} -2bc \cos(A)\\ a^{2}=9^{2} + 9^{2} – 2 \times 9 \times 9 \times \cos(80)\\ a^{2}=162-162 \cos(80)\\ a^{2}=133.8689952\\ a=11.57017697cm\]

Add the length of the arc and the chord.

\[\text{Length of the arc }+\text{ Length of the chord } = 4 \pi+11.57017697\\ =24.13654759\]

Clearly state your answer.

The question asked you to round the answer to $3$ decimal places.

Perimeter = $24.137cm$

Example 5: calculate the area of a segment without the angle of the segment being given

Calculate the area of the segment shown below. Give your answer to $1$ decimal place

Find the length of the radius.

Length of radius: $20cm$

Find the size of the angle creating the sector.

The angle of the sector, created by the two radii, is not given to you in this question. Here you can use the triangle created by the two radii and the chord to find the angle

You need to apply the cosine rule to find the size of the angle.

$A$ is the angle you are trying to find. You can therefore use the rearranged cosine rule to find the angle.

\[\cos{A}=\frac{b^{2}+c^{2}-a^{2}}{2 b c} \\ \cos{A}=\frac{20^{2}+20^{2}-28^{2}}{2 \times 20 \times 20} \\ \cos{A}=\frac{1}{50} \\ A=\cos^{-1}\left(\frac{1}{50}\right) \\ A=88.8540008^{\circ}\]

The size of the angle creating the sector (made by the two radii) is $88.854^{\circ}$ .

Find the area of the sector.

31.0159..+28=59.0159cm\[\text{Area of sector }=\frac{\theta}{360}\times \pi r^{2}\\ =\frac{88.854}{360} \times \pi \times 20^{2} \\ =310.15897\]

Area of sector: $310.15897cm^{2}$

Find the area of the triangle created by the radii and the chord.

\[\text{Area of triangle}=\frac{1}{2} a b \sin C \\ =\frac{1}{2} \times 20\times 20 \times\sin(88.854)\\ =199.95999…\]

Area of triangle: $199.95999…cm^{2}$

Subtract the area of the triangle from the area of the sector.

\[\text{Area of sector} – \text{Area of triangle } =310.15897-199.959..\\ =110.19897…\]

Clearly state your answer.

The question asked you to round your answer to $1$ decimal place

Area of segment: $110.19897cm^{2}= 110.2cm^{2} (1.d.p)$

Example 6: calculate the perimeter of a segment without the angle of the segment being given

Calculate the perimeter of the segment shown below. Give your answer to $1$ decimal place

Find the length of the radius.

Length of radius: $20cm$ (given to you in the question)

Find the size of the angle creating the sector.

The angle of the sector, created by the two radii, is not given to you in this question. Here you can use the triangle created by the two radii and the chord to find the angle

You need to apply the cosine rule to find the size of the angle.

$A$ is the angle you are trying to find. You can therefore use the rearranged cosine rule to find the angle.

\[\cos{A}=\frac{b^{2}+c^{2}-a^{2}}{2 b c} \\ \cos{A}=\frac{20^{2}+20^{2}-28^{2}}{2 \times 20 \times 20} \\ \cos{A}=\frac{1}{50} \\ \cos^{-1}\left(\frac{1}{50}\right) \\ A=88.8540008^{\circ}\]

The size of the angle creating the sector (made by the two radii) is $88.854^{\circ}$ .

Find the length of the arc of the segment.

\[\text{Arc length }=\frac{\theta}{360} \times 2 \pi r \\ =\frac{88.854}{360} \times 2 \pi \times 20 \\ =31.0159…\]

Length of arc: $31.0159cm$

Find the length of the chord of the segment.

Length of chord: $28cm$

Add the length of the arc and the chord.

Length of the arc + Length of chord = $31.0159.. + 28 = 59.0159cm$

Clearly state your answer.

The question asked you to round your answer to $1$ decimal place

Perimeter of segment: $59.0159...cm = 59.0 cm (1.d.p)$

Common misconceptions

Confusing the segment/sector

A segment is the area enclosed by the arc of a circle and a chord. A sector is the area enclosed by the arc of a circle and two radii.

Confusing the chord/diameter

A chord can cross a circle at any point, but a diameter but go through the centre of the circle.

Incorrect use of the cosine rule

Many mistakes are made when applying other rules within a segment question e.g the cosine rule. Take your time with these parts and regularly check that your answer makes sense within the context of the question.

Not including the chord length when finding the perimeter of a segment

Remember the perimeter of a shape is the sum of the lengths of each of the sides. Therefore the perimeter of a segment is made up the arc and the chord

Degrees and radians

Angles can be measured in both degrees and radians, however at GCSE we only use degrees.

Practice segment of a circle questions

36\pi \mathrm{cm}^{2}

72 cm^{2}

41.1 cm^{2}

41.097 cm^{2}

\text{Area of sector }=\frac{\theta}{360} \pi r^{2}\\ =\frac{90}{360}\times \pi \times 12^{2}\\ =36 \pi

\text{Area of triangle }=\frac{1}{2}ab \sin C\\ =\frac{1}{2}\times 12 \times 12 \sin(90)\\ =72

\text{Area of segment }=36 \pi – 72\\ =41.09733553\\ =41.1\mathrm{cm}^{2}

12\pi

40.97 cm

20.7cm

35.8 cm

\text{Arc length}=\frac{\theta}{360} \times 2 \pi r \\ =\frac{90}{360} \times 2 \pi \times 12 \\ =6 \pi

Length of cord:

a^{2}+b^{2}=c^{2} \\ 12^{2}+12^{2}=c^{2} \\ 144+144=c^{2} \\ 288=c^{2} \\ 12 \sqrt{2}=c

\text{Length of the arc }+\text{ Length of the chord } = 6\pi + 12 \sqrt{2}\\ =35.82011867\\ =35.8\mathrm{cm}

22.3 m^{2}

19.6m^{2}

25.1m^{2}

15.9m^{2}

\text{Area of sector }=\frac{\theta}{360} \pi r^{2}\\ =\frac{160}{360}\times \pi \times 4^{2}\\ =\frac{64}{9} \pi

\text{Area of triangle }=\frac{1}{2}ab \sin C\\ =\frac{1}{2}\times 4 \times 4 \sin(160)\\ =2.73616…

\text{Area of segment }=\frac{64}{9} \pi – 2.73616\\ =19.60405\\ =19.6\mathrm{m}^{2}

1.92 m

3.767 m

1.85 m

3.77 m

\text{Arc length}=\frac{\theta}{360} \times 2 \pi r \\ =\frac{55}{360} \times 2 \pi \times 2 \\ =\frac{11}{18} \pi

Length of cord:

a^{2}=b^{2} + c^{2} -2bc \cos(A)\\ a^{2}=2^{2} + 2^{2} – 2 \times 2 \times 2 \times \cos(55)\\ a^{2}=8-8 \cos(55)\\ a^{2}=3.411388509\\ a=1.846994453

\text{Length of the arc }+\text{ Length of the chord } =\frac{11}{18} \pi + 1.846994453\\ =3.76685663

14.21cm^{2}

25.40cm^2

11.19cm^{2}

18.66cm^{2}

First we need to find the angle using the cosine rule.

\cos{A}=\frac{b^{2}+c^{2}-a^{2}}{2 b c} \\ \cos{A}=\frac{5^{2}+5^{2}-8.5^{2}}{2 \times 5 \times 5} \\ \cos{A}=-\frac{89}{200} \\ A=\cos^{-1}\left(-\frac{89}{200}\right) \\ A=116.4233388^{\circ}

\text{Area of sector }=\frac{\theta}{360} \pi r^{2}\\ =\frac{116.423}{360}\times \pi \times 5^{2}\\ =25.39955844

\text{Area of triangle }=\frac{1}{2}ab \sin C\\ =\frac{1}{2}\times 5 \times 5 \sin(116.423)\\ =11.194165

\text{Area of segment }=25.39955844 – 11.194165\\ =14.20539344\\ =14.21\mathrm{cm}^{2}

22.0mm

16.5mm

8.52mm

22.5mm

First we need to find the angle using the cosine rule.

\cos{A}=\frac{b^{2}+c^{2}-a^{2}}{2 b c} \\ \cos{A}=\frac{7^{2}+7^{2}-8^{2}}{2 \times 7 \times 7} \\ \cos{A}=\frac{17}{49} \\ A=\cos^{-1}\left(\frac{17}{49}\right) \\ A=69.69980^{\circ}

\text{Arc length}=\frac{\theta}{360} \times 2 \pi r \\ =\frac{69.6998}{360} \times 2 \pi \times 7 \\ =8.515436986

Chord length: $8mm$

\text{Perimeter }=8.515436986+8\\ =16.515436986\\ =16.5\mathrm{mm}

Segment of a circle GCSE questions

1. The diagram shows a sector $OABC$ of a circle with centre $O$ .

(a) Calculate the length of the arc $ABC$ of the sector. Give your answer correct to $3$ significant figures.

(b) Calculate the area of the shaded segment $ABC$ . Give your answer correct to $3$ significant figures.

(7 marks)

Show answer

(a)

\frac{120}{360} \times \pi \times 20.8

(1)

21.781709

(1)

21.8 cm

(1)

(b)

Either $113.26\dots$ or $46.83$ seen

(1)

“113.26\dots” - “46.83”

(1)

66.430\dots

(1)

66.4 cm^{2}

(1)

2. The diagram shows a sector $OPRS$ of a circle with centre $O$ .

Calculate the area of the shaded segment $PRS$ .

Give your answer correct to $3$ significant figures.

(5 marks)

Show answer

Area of sector $= 22.34$

(1)

Area of triangle $= 20.569$

(1)

“22.340\dots” - “20.569”

(1)

=1.7710\dots

(1)

=1.77cm^{2}

(1)

3. The diagram shows a sector $OPRS$ of a circle with centre $O$ .

Calculate the area of the shaded segment $RST$ .

Give your answer correct to $3$ significant figures.

(5 marks)

Show answer

Area of sector $= 1954.76876\dots$

(1)

Area of triangle $= 1835.444\dots$

(1)

“1954.768\dots” - “1835.444”

(1)

119.324\dots

(1)

119cm^{2}

(1)

4. The diagram below shows a shaded segment.

(a) Find the area of the shaded segment. Give your answer correct to $3$ significant figures.

(b) Find the perimeter of the shaded segment. Give your answer correct to $3$ significant figures.

(9 marks)

Show answer

(a)

Angle at centre $= 112.88538$ … may be shown on diagram

(1)

Area of sector $= 141.85595\dots$

(1)

Area of triangle $= 66.332496\dots$

(1)

“141.85595” - “66.332496”

(1)

= 75.523454..

(1)

75.5cm^{2}

(1)

(b)

Length of arc $= 23.6426587\dots$

(1)

Length of chord $= 20$

(1)

“23.6426587” + 20

(1)

= 43.6426587

(1)

43.6cm

(1)

Learning checklist

You have now learned how to:

Identify and apply circle definitions and properties
Identify and apply circle definitions and properties, including a segment
Find the perimeter of a segment
Calculate areas of segments by applying trigonometry

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.