Arc of a circle

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

Parts of a circle Circumference of a circle Solving equations Sine rule Cosine rule Rounding numbers Square numbers and square roots

This topic is relevant for:

GCSE Maths Geometry and Measure 2D Shapes CSA

Arc Of A Circle

Here we will learn about the arc of a circle, including how to find the arc length and work backwards given the arc length to solve problems.

There are also arc of a circle worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is an arc of a circle?

An arc of a circle is a portion of the circumference of a circle.

In GCSE mathematics the arc of a circle can be used to define angles and lengths.

The arc of a circle would be the curved edge of a sector or segment.

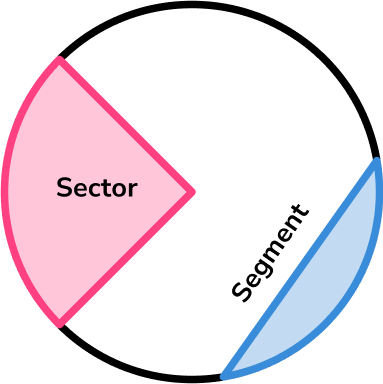
There are circle theorems that are defined using arcs of the circle.

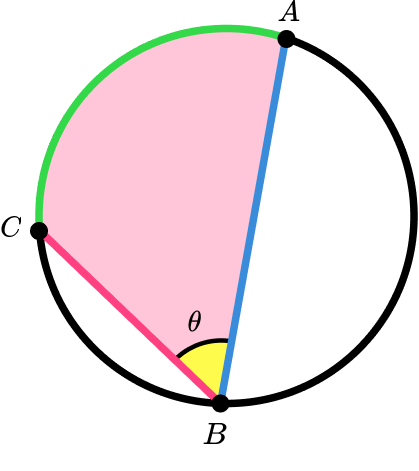
For example, $\theta$ is the angle subtended by arc $AC.$

We can find the length of an arc if we know the angle of the sector.

What is an arc of a circle?

Calculating the arc length

The arc length is a fraction of the circumference of the circle.

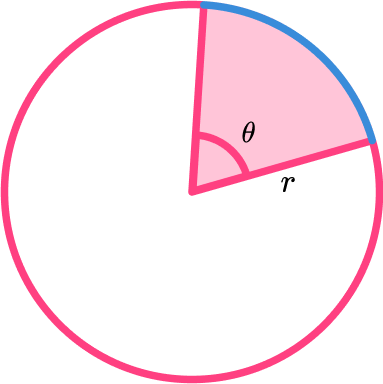
The fraction will be $\frac{\theta}{360},$ if $\theta$ is the angle of the sector.

The arc length formula is,

\text{Arc length } = \frac{\theta}{360} \times \pi\times d

\theta = \text{ angle of the sector}

d = \text{ diameter of the circle}

\text{Arc length } = \frac{\theta}{360} \times 2\times\pi \times r

\theta = \text{ angle of the sector}

r = \text{ radius of the circle}

How to calculate the arc length

In order to calculate the arc length:

Find the length of the radius.
Find the size of the angle creating the sector.
Substitute the values you know into the formula for the arc length.
Calculate the answer.

Explain how to calculate the arc length

Arc of a circle worksheet

Get your free arc of a circle worksheet of 20+ questions and answers. Includes reasoning and applied questions.

COMING SOON

Arc of a circle worksheet

Get your free arc of a circle worksheet of 20+ questions and answers. Includes reasoning and applied questions.

COMING SOON

Arc of a circle is part of our series of lessons to support revision on circles, sectors and arcs. You may find it helpful to start with the main circles, sectors and arcs lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Calculating the arc length examples

Example 1: calculate the arc length given the angle

Calculate the arc length of the sector shown below.

Give your answer to $3$ significant figures.

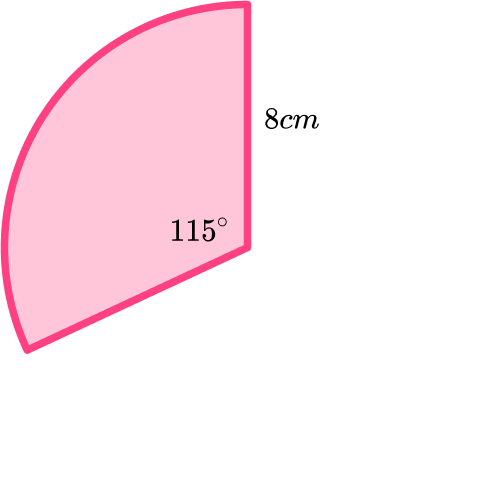
Find the length of the radius/diameter.

Radius $= 8 \ cm$

2Find the size of the angle creating the sector.

Angle $= 115^{\circ}$

3Substitute the values you know into the formula for the arc length.

As you know the radius you can use the formula which has $‘r’$ as a variable.

\begin{aligned} \text{Arc length } &=\frac{\theta}{360} \times 2\times\pi \times r \\\\ &=\frac{115}{360} \times 2\times\pi \times 8 \\\\ &=\frac{46}{9} \pi \end{aligned}

4Calculate the answer.

The question asks you to round your answer to $3$ significant figures.

\begin{aligned} \text{Arc length } &=\frac{46}{9}\pi \ cm \\\\ &=16.0570...cm \end{aligned}

The arc measures $=16.1 \ cm$ .

Example 2: calculate the arc length not given the angle

Calculate the arc length of the sector shown below.

Give your answer to $3$ significant figures.

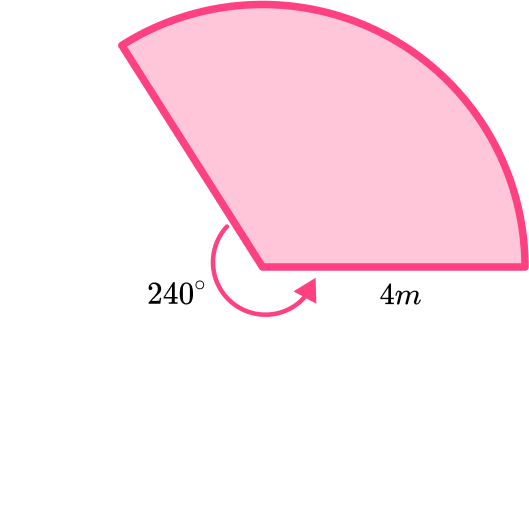
Find the length of the radius.

Radius $= 4 \ m$

Although we can use the radius or diameter as long as we use the correct formula for each.

Find the size of the angle creating the sector.

The angle creating the sector is the angle included between the two radii.

To find it in this case we need to use the angle fact, angles around a point add to $360^{\circ}.$

$360-240=120$

The angle creating the sector is $120^{\circ}.$

Substitute the values you know into the formula for the arc length.

\begin{aligned} \text { Arc length }&=\frac{\theta}{360} \times 2 \times \pi \times r \\\\ &=\frac{120}{360} \times 2 \times \pi \times 4 \end{aligned}

Calculate the answer.

\begin{aligned} &=8.37758041 \\\\ &=8.38 \mathrm{~m} \end{aligned}

Example 3: finding the arc length not given the radius or angle

Below is a sector of a circle.

The diameter of the circle is $12 \ cm.$

Calculate the arc length.

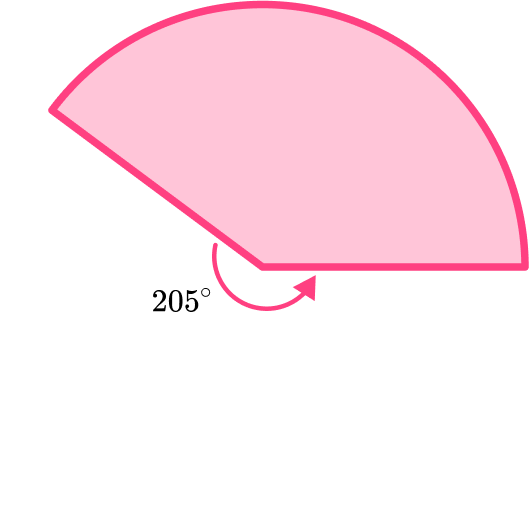
Find the length of the radius.

Diameter $= 12 \ cm$

The radius is half of the diameter, so the radius $= 6 \ cm.$

Although we can use the radius or diameter as long as we use the correct formula for each.

Find the size of the angle creating the sector.

The angle creating the sector is the angle included between the two radii.

To find it in this case we need to use the angle fact, angles around a point add to $360^{\circ}.$

$360-205=155$

The angle creating the sector is $155^{\circ}.$

Substitute the values you know into the formula for the arc length.

\begin{aligned} \text { Arc length }&=\frac{\theta}{360} \times 2 \times \pi \times r \\\\ &=\frac{155}{360} \times 2 \times \pi \times 6 \end{aligned}

Calculate the answer.

\begin{aligned} &=16.23156204 \\\\ &=16.2 \mathrm{~cm} \end{aligned}

Common misconceptions

Finding the length of the circumference not the length of the arc

Remember to find the fraction of the circle that makes the arc not just the circumference of the whole circle.

For example,

Use $\frac{\theta}{360} \times \pi\times d$

or $\frac{\theta}{360} \times 2\times\pi \times r$ .

Not $\pi\times d$

or $2\times\pi \times r.$

Incorrect angle unit set on calculator

At GCSE all angles are measured in degrees. Make sure that your calculator has a small $‘d’$ for degrees at the top of the screen rather than an $‘r’$ for radians – these are not used until A Level.

Practice arc of a circle questions

Segment

Major arc

Minor arc

Sector

Part of the circumference is called an arc. The red line is more than half of the circumference, so it is a major arc.

8 \pi \ cm

8\pi+8 \ cm

4\pi \ cm

2 \pi \ cm

The length of the curved edge of a semicircle can be found by calculating $\pi d \div 2.$

9.4 \ cm

28.3 \ cm

18.8 \ cm

37.7 \ cm

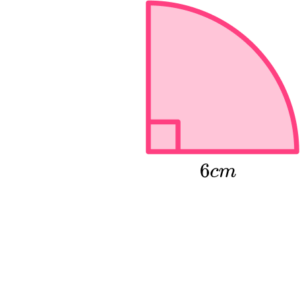
The length of the curved edge of a quarter-circle can be found by calculating $\pi d \div 4.$

2.4 \ cm

7.3 \ cm

17.1 \ cm

4.9 \ cm

Substituting the values we know into the formula for the arc length,

\begin{aligned} \text{Arc length } &=\frac{\theta}{360} \times 2 \times \pi \times r \\\\ &=\frac{40}{360} \times 2 \times \pi \times 7 \\\\ &=4.886921906 \mathrm{~cm} \end{aligned}

16.8 \ cm

4.2 \ cm

8.4 \ cm

12.6 \ cm

Substituting the values we know into the formula for the arc length, remembering $\theta =60^{\circ}$ because this is an equilateral triangle.

\begin{aligned} \text{Arc length } &=\frac{\theta}{360} \times 2 \times \pi \times r \\\\ &=\frac{60}{360} \times 2 \times \pi \times 8 \\\\ &=8.37758041 \mathrm{~cm} \end{aligned}

150^{\circ}

210^{\circ}

60^{\circ}

30^{\circ}

Substituting the values we know into the formula for arc length,

\frac{\theta}{360} \times 2 \times \pi \times 12=10 \pi

Solving for the angle $\theta,$

\theta=150^{\circ}.

Arc of a circle GCSE questions

1. A sector has a radius of $15 \ cm$ and an angle of $120^{\circ}.$ Find the length of the arc in terms of $\pi.$

(2 marks)

Show answer

Use of $\frac{\theta}{360} \times \pi d$ .

(1)

10 \pi

(1)

2. The sector has an angle of $50^{\circ}$ and an arc length of $25 \ cm.$ Find the radius of the sector in centimetres to the nearest millimetre.

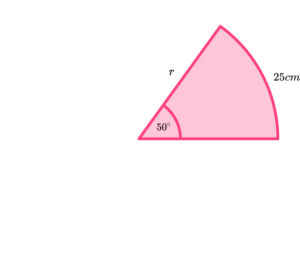
Arc of a Circle GCSE question 2

(3 marks)

Show answer

$25=\frac{50}{360} \times \pi d$ (or equivalent).

(1)

Diameter $= 57.29\dots$

(1)

Radius $= 28.6 \ cm$

(1)

3. A metal sector with radius $6 \ cm$ and angle $250^{\circ}$ is used to form an open cone, as shown.

Calculate the radius, $r,$ of the cone formed from the sector.

Arc of a Circle GCSE question 3

(4 marks)

Show answer

Use of $\frac{250}{360} \times 12 \pi$ .

(1)

Arc length $= 26.1799\dots$

(1)

\pi r^{2}=26.1799…

(1)

r=2.89 \ cm

(1)

Learning checklist

You have now learned how to:

Identify and apply circle definitions and properties, including tangent, arc, sector and segment

Calculate the length of an arc

Calculate a property of a circle given the length of an arc

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.