Sine rule

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

Learn more

In order to access this I need to be confident with:

Trigonometric functions Solving equations Rearranging equations Rounding decimals Significant figures Exact trig values

This topic is relevant for:

GCSE Maths Geometry and Measure Trigonometry Trigonometry Formula

Sine Rule

Here we will learn about the sine rule including how to use the sine rule to find missing sides and angles in triangles.

There are also sine rule worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

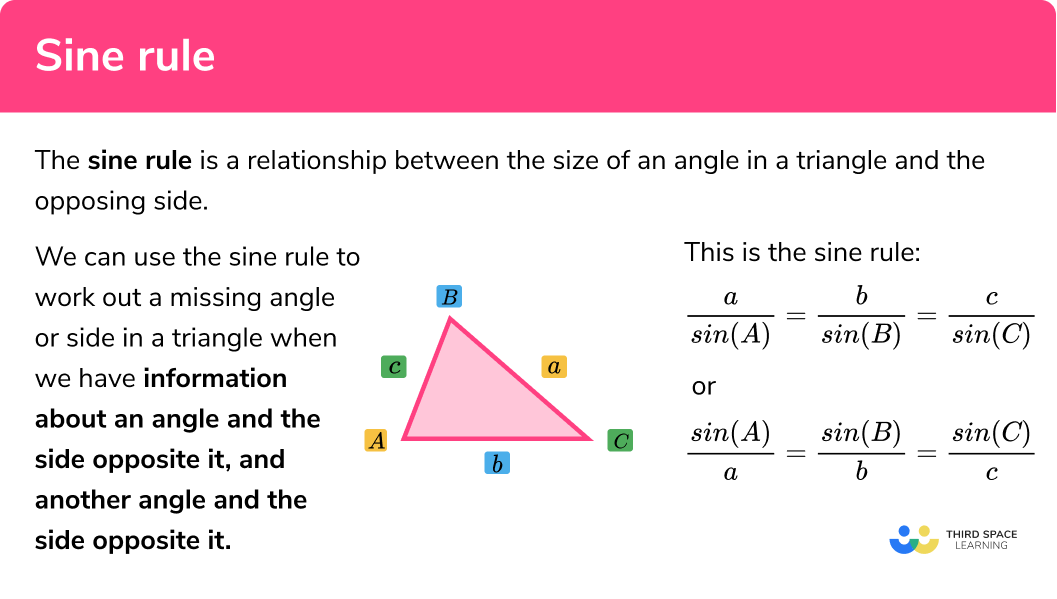
What is the sine rule?

The sine rule (or the law of sines) is a relationship between the size of an angle in a triangle and the opposing side.

We can use the sine rule to work out a missing angle or side in a triangle when we have information about an angle and the side opposite it, and another angle and the side opposite it.

This is the sine rule:

\[\frac{a}{\sin (A)}=\frac{b}{\sin (B)}=\frac{c}{\sin (C)}\]

Even though there are three relationships in a triangle between the three angles and their opposite sides, we only need to use two of them for the sine rule.

It would look something like this:

\[\frac{a}{\sin (A)}=\frac{b}{\sin (B)}\]

What is the sine rule

How can I use the sine rule?

We can use the sine rule to find missing sides and angles when we have information about a pair of angles and their opposite sides.

1 Label each angle (A, B, C) and each side (a, b, c) of the triangle.

Capital letters A, B, C, are used to label vertices (corners) of a triangle and lower-case letters, a, b, c, are used to label the sides of a triangle.

The opposite angle is the same letter as the opposite side.

It does not matter which sides are a, b and c, but the capital letter for the vertex must be opposite the same letter on the side for the sine relationship to work.

2 State the sine rule then substitute the given values into the equation.

Now that we know which sides and angles we have, we need to substitute this information into the sine rule. We can then solve this equation to find the missing side or angle.

As these are calculated slightly differently, we can rearrange the sine rule to suit the part of the triangle we are trying to find. Here are the two versions.

To find a missing angle:

$\frac{\sin (A)}{a}=\frac{\sin (B)}{b}$

To find a missing side:

$\frac{a}{\sin (A)}=\frac{b}{\sin (B)}$

One equation is a rearrangement of the other.

Top tips:

When we are finding a missing angle, we put the angles on top (sin A, sin B, sin C)

When we are finding a missing side, we put the sides on top (a, b, c)

3 Solve the equation.

Once everything is substituted into the sine rule we can solve the equation to calculate the unknown side or angle.

How to find a missing side or a missing angle of a triangle using the sine rule

In order to find a missing side of a triangle using the sine rule:

Label each angle (A, B, C) and each side (a, b, c) of the triangle.
State the sine rule then substitute the given values into the equation.
Solve the equation.

Explain how to find a missing side or a missing of a triangle using the sine rule

Sine rule worksheet

Get your free sine rule worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Sine rule worksheet

Get your free sine rule worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Sine rule examples (missing side)

Example 1: finding a missing side of a triangle

Calculate the length AB. Write your answer to two decimal places.

Label each angle (A, B, C) and each side (a, b, c) of the triangle.

2 State the sine rule then substitute the given values into the equation.

Here we know side a and we want to find the length of c, therefore we can state:

\[\begin{aligned} \frac{a}{\sin (A)}&=\frac{c}{\sin (C)}\\\\ \frac{6}{\sin (55)}&=\frac{c}{\sin (73)} \end{aligned} \]

3 Solve the equation.

\begin{array}{l} \\\frac{6}{\sin (55)}=\frac{c}{\sin (73)}\\\\ c=\frac{6}{\sin (55)}\times\sin(73)\\\\ c=\frac{6\sin(73)}{\sin (55)}\\\\ c=7.00\quad(2d.p.) \end{array}

Here, the length AB = 7.00cm (2d.p.).

Example 2: finding a missing side of a triangle

Calculate the length BC. Write your answer to two decimal places.

Label each angle (A, B, C) and each side (a, b, c) of the triangle.

State the sine rule then substitute the given values into the equation.

Here we know side c and we want to find the length of a, therefore we can state:

\begin{aligned} \\\frac{a}{\sin (A)}&=\frac{c}{\sin (C)}\\ \\\frac{a}{\sin (41)}&=\frac{3.4}{\sin (27)}\\ \end{aligned}

Solve the equation.

\begin{array}{l} \frac{a}{\sin (41)}=\frac{3.4}{\sin (27)}\\ \\a=\frac{3.4}{\sin (27)}\times\sin(41)\\ \\a=\frac{3.4\sin(41)}{\sin (27)}\\ \\a=4.91\quad(2d.p.) \end{array}

Here, the length BC = 4.91cm (2d.p.).

Example 3: finding a missing side of a triangle

Calculate the length AC. Write your answer to two decimal places.

Label each angle (A, B, C) and each side (a, b, c) of the triangle.

State the sine rule then substitute the given values into the equation.

Here we know side a and we want to find the length of b, therefore we can state:

\begin{aligned} \\\frac{a}{\sin (A)}&=\frac{b}{\sin (B)}\\ \\\frac{10.8}{\sin (81)}&=\frac{b}{\sin (48)}\\ \end{aligned}

Solve the equation.

\begin{array}{l} \\\frac{10.8}{\sin (81)}=\frac{b}{\sin (48)}\\ \\b=\frac{10.8}{\sin (81)}\times\sin(48)\\ \\b=\frac{10.8\sin(48)}{\sin (81)}\\ \\b=8.13\quad(2d.p.) \end{array}

Here, the length AC = 8.13cm (2d.p.).

Sine rule examples (missing angle)

Example 4: finding a missing angle of a triangle

Calculate the size of the missing angle θ. Write your answer to one decimal place.

Label each angle (A, B, C) and each side (a, b, c) of the triangle

State the sine rule then substitute the given values into the equation

Here we know the angle at B and we want to find the angle at C, therefore we can state:

\begin{aligned} \\\frac{\sin (B)}{b}&=\frac{\sin (C)}{c}\\ \\\frac{\sin (86)}{9.5}&=\frac{\sin (\theta)}{4.7}\\ \end{aligned}

Solve the equation.

\begin{array}{l} \\\frac{\sin (86)}{9.5}=\frac{\sin (\theta)}{4.7}\\ \\\sin (\theta)=\frac{\sin (86)}{9.5}\times4.7\\ \\\sin (\theta)=0.493531688…\\ \\\theta=\sin ^{-1}(0.493531688)\\ \\\theta=29.6^{\circ}\quad(1d.p.) \end{array}

Here, the angle

\[\theta = 29.6^{\circ} (2d.p.).\]

Example 5: finding a missing angle of a triangle

Calculate the size of the missing angle θ. Write your answer to one decimal place.

Label each angle (A, B, C) and each side (a, b, c) of the triangle.

State the sine rule then substitute the given values into the equation.

Here we know the angle at B and we want to find the angle at C, therefore we can state:

\begin{aligned} \\\frac{\sin (B)}{b}&=\frac{\sin (C)}{c}\\ \\\frac{\sin (10)}{1.5}&=\frac{\sin (\theta)}{7.6}\\ \end{aligned}

Solve the equation.

\begin{array}{l} \\\frac{\sin (10)}{1.5}=\frac{\sin (\theta)}{7.6}\\ \\\sin (\theta)=\frac{\sin (10)}{1.5}\times7.6\\ \\\sin (\theta)=0.8798174335…\\ \\\theta=\sin ^{-1}(0.8798174335)\\ \\\theta=61.6^{\circ}\quad(1d.p.) \end{array}

Here, the length AB = 61.6º (1d.p.).

Example 6: finding a missing angle of a triangle

Calculate the size of the missing angle θ.

Label each angle (A, B, C) and each side (a, b, c) of the triangle.

State the sine rule then substitute the given values into the equation.

Here we know the angle at B and we want to find the angle at A, therefore we can state:

\begin{aligned} \\\frac{\sin (A)}{a}&=\frac{\sin (B)}{b}\\ \\\frac{\sin (\theta)}{5}&=\frac{\sin (60)}{5}\\ \end{aligned}

Solve the equation.

\begin{array}{l} \\\frac{\sin (\theta)}{5}=\frac{\sin (60)}{5}\\ \\\sin (\theta)=\frac{\sin (60)}{5}\times5\\ \\\sin (\theta)=\frac{\sqrt{3}}{2}\\ \\\theta=\sin ^{-1}(\frac{\sqrt{3}}{2})\\ \\\theta=60^{\circ}\quad \end{array}

Here, the length AB = 60º.

Common misconceptions

Incorrect labelling of the triangle

This can cause a follow through error when substituting values into the equation. For example, this triangle has been incorrectly labelled with the side next to the angle.

This will have an impact on the formula for the sine rule as it will look like this, and not the correct way in example 5.

Mixing up when to use the sine and inverse sine function

When finding a side, use the sine function. When finding a missing angle, you need to use the inverse sine function.

Using the sine rule to find a missing side when you do not know the value of two angles in the triangle

In order to use the sine rule we need to have sides and angles that are opposite each other. If we are finding a missing side then we need to know two angles and one of the sides opposite, we can use this information to find the side that is opposite the other angle.

Rounding the decimal too early

This can lose accuracy marks. Always use as many decimal places as possible throughout the calculation, then round your solution.

Using the incorrect set up for the sine rule formula

It should not be too difficult to rearrange the formula once you have substituted the values, however small errors will make an impact on your solution.

Cancelling out sine functions

For example, when calculating the value for a in example 2, the following calculation error is made.

\begin{array}{l} \\\frac{a}{\sin (41)}=\frac{3.4}{\sin (27)}\\ \\a=\frac{3.4}{\sin (27)}\times\sin(41)\\ \\a=\frac{3.4\sin(41)}{\sin (27)}\\ \\a=\frac{3.4\times41}{27}\\ \\a=5.16\quad(2dp) \end{array}

This is incorrect because sine is a function so we cannot do this.

Be aware of the ambiguous case for the sine rule

Due to the nature of the sine function, there can be multiple solutions to a question.
Take for example sin(60). This gives the same solution as sin(120) (See Trigonometric Graphs for further details).

A calculator is programmed to return the first value for the angle but you should be aware that another solution can exist for an obtuse angle.

To check if the calculator has returned the solution you need, there are 3 simple checks that can be done.

Sin(θ) = 1. This case only has one solution, θ = 90º (a right angle triangle).
The sum of the angles is greater than 180º. This would make an impossible triangle.
The angle opposite a longer side must be larger. Compare the values for the sides of the triangle a, b, and c with their counterpart angles A, B, and C. The larger side will always be opposite a larger angle.

Sine rule is part of our series of lessons to support revision on trigonometry. You may find it helpful to start with the main trigonometry lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Practice sine rule questions

6.29cm

4.95cm

6.07cm

6.11cm

Sine rule practice question 1 answer

\begin{array}{l} \frac{a}{\sin(A)}=\frac{c}{\sin(C)}\\\\ \frac{a}{\sin(48)}=\frac{5.5}{\sin(42)}\\\\ a=\frac{5.5}{\sin(42)} \times \sin(48)\\\\ a=6.11 \mathrm{~cm} \end{array}

88.02mm

34.37mm

99.69mm

88.21mm

Sine Rule Practice Question 2 Answer

\begin{array}{l} \frac{b}{\sin(B)}=\frac{c}{\sin(C)}\\\\ \frac{55}{\sin(32)}=\frac{c}{\sin(58)}\\\\ a=\frac{55}{\sin(32)} \times \sin(58)\\\\ a=88.02 \mathrm{~mm} \end{array}

7.16cm

6.09cm

5.83cm

7.47cm

Sine Rule Practice Question 3 Answer

\begin{array}{l} \frac{a}{\sin(A)}=\frac{c}{\sin(C)}\\\\ \frac{6.6}{\sin(60)}=\frac{c}{\sin(53)}\\\\ a=\frac{6.6}{\sin(60)} \times \sin(53)\\\\ a=6.09\mathrm{~cm} \end{array}

66^{\circ}

70^{\circ}

0.016^{\circ}

0.93^{\circ}

Sine Rule Practice Question 4 Answer

\begin{array}{l} \frac{\sin(B)}{b}=\frac{\sin(C)}{c}\\\\ \frac{\sin (\theta)}{7.4}=\frac{\sin (68)}{7.3}\\\\ \sin (\theta)=\frac{\sin (68)}{7.3}\times7.4\\\\ \sin (\theta)=0.9398850033…\\\\ \theta=\sin^{-1}(0.9398850033)\\\\ \theta=70^{\circ}\quad(2 s.f.) \end{array}

27.58^{\circ}

51.90^{\circ}

28.16^{\circ}

32.51^{\circ}

Sine Rule Practice Question 5 Answer

\begin{array}{l} \frac{\sin(A)}{a}=\frac{\sin(C)}{c}\\\\ \frac{\sin (62)}{8.2}=\frac{\sin (\theta)}{4.3}\\\\ \sin (\theta)=\frac{\sin (62)}{8.2}\times4.3\\\\ \sin (\theta)=0.4630091036…\\\\ \theta=\sin^{-1}(0.4630091036)\\\\ \theta=27.58^{\circ}\quad(2 d.p.) \end{array}

72^{\circ}

22.5^{\circ}

64.7^{\circ}

55.4^{\circ}

Sine Rule Practice Question 6 Answer

\begin{array}{l} \frac{\sin(A)}{a}=\frac{\sin(B)}{b}\\\\ \frac{\sin (\theta)}{10}=\frac{\sin (36)}{6.5}\\\\ \sin (\theta)=\frac{\sin (36)}{6.5}\times10\\\\ \sin (\theta)=0.9042850035…\\\\ \theta=\sin ^{-1}(0.9042850035)\\\\ \theta=64.72^{\circ}\quad(3s.f.) \end{array}

Sine rule GCSE exam questions

1. In triangle $ABC, AC = 8.5cm, BC = 23cm$ and angle $BAC = 80^{\circ}.$

Calculate the size of the angle marked $x.$

Give your answer to $1$ d.p.

Sine Rule (Exam Question 1)

(3 marks)

Show answer

\frac{\sin(x)}{8.5}=\frac{\sin(80)}{23}

(1)

\begin{aligned} \sin(x)&=\frac{\sin(80)}{23} \times 8.5\\\\ \sin(x)&=0.364… \end{aligned}

(1)

\begin{aligned} x&=\sin^{-1}(0.364…)\\\\ x&=21.3^{\circ} \end{aligned}

(1)

2. Work out the size of angle $BCD$ .

Sine Rule (Exam Question 2)

(5 marks)

Show answer

\frac{BD}{\sin(77)}=\frac{14}{\sin(51)}

(1)

\begin{aligned} BD&=\frac{14}{\sin(51)} \times \sin(77)\\\\ BD&= 17.553\mathrm{cm} \end{aligned}

(1)

\frac{sin(\theta)}{17.55}=\frac{sin(82)}{30}

(1)

\begin{aligned} \sin(\theta)&=\frac{sin(82)}{30} \times 17.55\\\\ sin(\theta)&=0.579… \end{aligned}

(1)

\begin{aligned} \theta&=sin^{-1}(0.579…)\\\\ \theta&=35.4^{\circ} \end{aligned}

(1)

3. Calculate the length $AB.$

Give your answer to $1$ d.p.

Sine Rule (Exam Question 3)

(4 marks)

Show answer

\begin{array}{l} \text{Angle ABE}=42^{\circ} \text{ (Alternate angles are equal)}\\\\ \text{Angle AEB: }180-46-42=92^{\circ} \end{array}

(1)

\frac{AB}{\sin(92)}=\frac{17}{\sin(46)}

(1)

AB=\frac{17}{\sin(46)} \times \sin(92)

(1)

AB=23.6cm

(1)

Learning checklist

You have now learned how to:

know and apply the sine rule to find unknown lengths and angles

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.