One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
Circumference of a circle Solving equations Sine rule Cosine rule Rounding numbers Squares and square rootsThis topic is relevant for:

Arc Length
Here we will learn about calculating arc length including how to identify the arc of a circle (minor and major), form and use the formula for the arc length of a circle and calculate the arc length in various scenarios.
There are also arc length worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
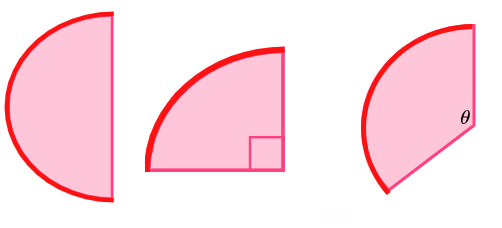
What is the arc length?
The arc length is a portion of the circumference of the circle
Major arc: a major arc is greater than half the circumference.
Minor arc: a minor arc is less than half the circumference.
Arc length = \frac{\theta}{360} \times \pi\times d
θ – angle of the sector
d – diameter of the circle
Or
Arc length = \frac{\theta}{360} \times 2\times\pi \times r
θ- angle of the sector
r – radius of the circle
What is the arc length?

How to find the arc length of a circle
In order to find the arc length you need to be able to find the circumference of a circle. This is because the arc length is a portion of the circle’s circumference. ‘How much’ of the circle is decided by the angle created by the two radii.
The sum of the angles around a point is equal to 360°
Therefore, the arc length is the fraction of the circle’s circumference created by the sector.
The angle is out of 360 or \frac{\theta}{360} , where θ (theta) represents the angle, so we can multiply this by the circumference to calculate the arc length.
NOTE: At GCSE all angles are measured in degrees. Make sure that your calculator has a small ‘d’ for degrees at the top of the screen rather than an ‘r’ for radians- these are not used until A Level.
Arc length formula:
Arc length = \frac{\theta}{360} \times \pi\times d
θ – angle of the sector
d – diameter of the circle
Or
Arc length = \frac{\theta}{360} \times 2\times\pi \times r
θ – angle of the sector
r – radius of the circle
In order to solve problems involving the arc length you should follow the below steps:
- Find the length of the radius/diameter.
- Find the size of the angle creating the arc of the sector.
- Substitute the value of the radius/diameter and the angle into the formula for the arc length.
- Clearly state your answer.
How to find the arc length of a circle

Arc length worksheet

Get your free arc length worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Arc length worksheet

Get your free arc length worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on circles, sectors and arcs
Arc length is part of our series of lessons to support revision on arc of a circle and circles, sectors and arcs. You may find it helpful to start with the main circles, sectors and arcs lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Arc length examples
Example 1: calculate the arc length (quadrant)
Calculate the arc length of the sector shown below. Give your answer to 3 decimal places.
- Find the length of the radius/diameter.
The radius of a circle is the length of the line segment from the centre of the circle to the circumference.
Here the radius = 6cm
2Find the size of the angle creating the arc of the sector.
Angle = 90° . Shown by the symbol of the right angle.
3Substitute the value of the radius/diameter and the angle into the formula for the arc length.
As you know the radius you can use the formula which has ‘r’ as a variable.
4Clearly state your answer.
The question asked you to round your answer to 3 decimal places:
Remember the arc length (length of a curve on the circumference) is a measure of distance and, therefore, the units are not squared.
Example 2: calculate the arc length (semicircle)
Calculate the arc length of the semicircle shown below. Give your answer in terms of 𝜋.
Find the length of the radius/diameter.
Diameter = 24cm
Find the size of the angle creating the arc of the sector.
Angle = 180° . This is because the shape shown is a semicircle. Therefore, the angle of the straight line is 180 degrees.
Substitute the value of the radius/diameter and the angle into the formula for the arc length.
As you know the radius you can use the formula which has ‘d’ as a variable.
Clearly state your answer.
The question asked you to round your answer in terms of pi:
Arc length = 12\pi cm
Remember the arc length (length of the curve on a circumference) is a measure of distance and, therefore, the units are not squared.
Example 3: calculate the arc length (with an angle given)
Calculate the arc length of the sector shown below. Give your answer to 3 significant figures.
Find the length of the radius/diameter.
Radius = 8cm
Find the size of the angle creating the sector.
Angle = 115°
Substitute the value of the radius/diameter and the angle into the formula for the arc length.
As you know the radius you can use the formula which has ‘r’ as a variable.
Clearly state your answer.
The question asked you to round your answer to 3 significant figures:
Example 4: calculate the arc length (the angle is not given)
Calculate the arc length of the sector AOB below.
The length of the radius (OB) is 9cm
The length of a chord (AB) is 10cm .
Give your answer to 2 decimal places.
Find the length of the radius.
Radius = 9cm
Find the size of the angle creating the sector.
In this example you are not given the angle of the sector, you need to calculate it first. Here you can use the triangle created by the two radii and the chord to find the angle:
In this example, you need to apply the cosine rule to find the angle.
a^2=b^2+c^2-2bcCos(A)
A is the angle you are trying to find. You can therefore use the rearranged cosine rule to find the angle.
The size of the angle creating the sector (made by the two radii) is 67.498° .
Substitute the value of the radius/diameter and the angle into the formula for the arc length.
As you know the radius you can use the formula which has ‘r’ as a variable.
Clearly state your answer.
The question asked you to round your answer to 2 decimal places:
How to solve problems involving an arc length
Sometimes you may be given the arc length of the sector and asked to find a property of the circle such as the radius.
In this case you need to ‘reverse’ the process.
- Clearly state which of the properties you know and do not know (e.g. radius, angle of sector, arc length of sector)
- Using the formula for the arc length create an equation and solve for the unknown property you have been asked to find.
- Clearly state your answer.
Solving problems involving an arc length examples
Example 5: finding the radius given the arc length of the sector
The sector below has an arc length of 20cm and an angle of 125°.
Calculate the length of x.
Give you answer to 2 decimal places.
Clearly state which of the properties you know and do not know (e.g. radius, angle of sector, arc length of sector).
Radius = x
Angle of sector = 25°
Arc length = 20cm
Using the formula for the arc length create an equation and solve for the unknown property you have been asked to find.
You are trying to find the radius so use the formula with ‘r’ as the variable
Clearly state your answer.
The question asks you to give your answer to 2 decimal places:
Example 6: finding the angle of a sector given the arc length of the sector
The sector below has an arc length of 62cm and a radius of 18.5.
Calculate the length of x.
Give you answer to 2 decimal places.
Clearly state which of the properties you know and do not know (e.g. radius, angle of sector, arc length of sector).
Radius = 18.5
Angle of sector = x°
Arc length = 62cm
Using the formula for the arc length create an equation and solve for the unknown property you have been asked to find.
You are trying to find the radius so use the formula with ‘r’ as the variable
Clearly state your answer.
The question asks you to give your answer to 2 decimal places:
Common misconceptions
- Finding the length of the circumference not the length of the arc
Remember to find the fraction of the circle that makes the arc not just the circumference of the whole circle.
E.g.
Use
\frac{\theta}{360} \times \pi\times d
Or
\frac{\theta}{360} \times 2\times\pi \times r
Not
\pi\times d
Nor
2\times\pi \times r- Incorrect use of the cosine rule
Many mistakes are made when applying other rules within an arc question (e.g. the cosine rule). Take your time and regularly ask if your answer makes sense within the context of the question.
Have a look at our cosine rule lesson for more practice.
- Incorrect Units
Remember the arc is a length and therefore the units will not be squared.
Practice arc length questions
1. The circumference of a circle is 24cm . A sector within the same circle creates an arc of 6cm . What is the angle of the sector?




\begin {aligned}
\frac{arc length}{circumference}=\frac{6cm}{24cm} \\=\frac{1}{4}
\end{aligned}
\frac{1}{4} of the circumference
Therefore, it is a quarter of the circle, so the angle is 90^{\circ}
2. Is the arc in question 1 a minor or major arc?
Minor arc

Major arc

The arc length is less than half the circumference. Therefore, it is a minor arc.
3. Calculate the arc length of this sector, in terms of pi:




4. Calculate the arc length of this semi circle in terms of pi:




5. Calculate the arc length of this sector in terms of pi:




6. Calculate the arc length of this sector in terms of pi:




Arc length GCSE questions
1. The diagram shows a sector of a circle with centre O .
The radius of the circle is 13cm .
The angle of the sector is 150^{\circ}
Calculate the arc length, give your answer correct to 3 significant figures.
(3 marks)
\frac{150}{360} \times 2\times\pi \times 13
(1)
34.0339
(1)
34.0
(1)
2. The diagram shows a sector of a circle with centre O .
The radius of the circle is 6.5cm .
The acute angle AOB is 70^{\circ} .
Calculate the arc length sector, give your answer correct to 3 significant figures.
(3 marks)
\frac{290}{360} \times 2\times\pi \times 6.5
(1)
32.899
(1)
32.9
(1)
3. The diagram shows a sector of a circle with centre O .
The radius of the circle is 4.9cm .
The acute angle AOB is 60^{\circ} .
Calculate the arc length sector, give your answer correct to 2 decimal places.
\frac{60}{360} \times 2\times\pi \times 4.9
(1)
5.1312…
(1)
5.13
(1)
4. Below is a sector of a circle with an arc length of 6\pi cm and a radius of 10cm . Find the size of the angle labelled x .
(3 marks)
Correct attempt to form an equation for the arc length
6\pi=\frac{x}{360} \times 2 \times {\pi} \times 10
(1)
Attempt to solve equation for x , with one step completed correctly
\begin{aligned}
6&=\frac{x}{360} \times 20 \\
0.3&=\frac{x}{360}
\end{aligned}
(1)
108
(1)
5. The sector below has an arc length of 30cm .
Calculate the length of x .
Give you answer to 2 decimal places.
(4 marks)
Correct attempt to form an equation for the arc length
30=\frac{135}{360} \times 2 \times {\pi} \times x
(1)
Attempt to solve equation for x , with one step completed correctly
\begin{aligned}
80&=2 \times \pi \times x \\
40&=\pi \times x
\end{aligned}
(1)
12.732…
(1)
12.73
(1)
Learning checklist
You have now learned how to:
- Identify and apply circle definitions and properties, including: centre, radius, chord, diameter, circumference
- Identify and apply circle definitions and properties, including tangent, arc, sector and segment
- Calculate the length of an arc
- Calculate a property of a circle given the length of an arc
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.