GCSE Tutoring Programme
Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.
In order to access this I need to be confident with:
Arithmetic Adding decimals Subtracting decimals Parallel and perpendicular lines Collecting like terms Solving equations Types of triangles Types of quadrilateralsThis topic is relevant for:

Angles
Here we will learn about angles, including angle rules, angles in polygons and angles in parallel lines.
There are also angles worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
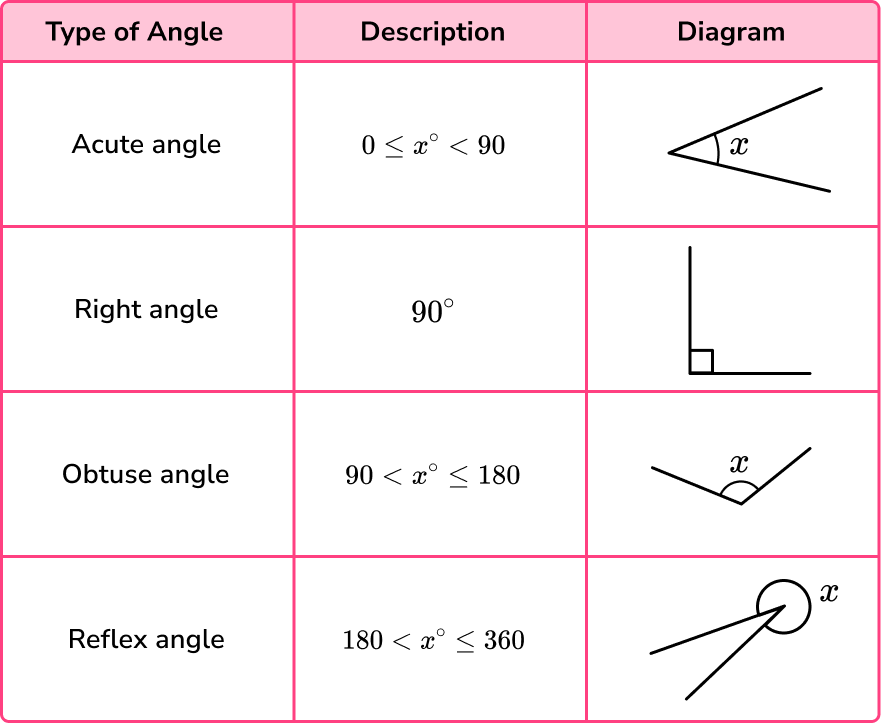
What are angles?
Angles measure the amount of turn required to change direction. At GCSE we can measure angles using a protractor using degrees. If the diagram is not drawn to scale we can determine missing angles by using angle facts (also referred to as angle properties or angle rules).
There can be multiple different approaches to find a missing angle.
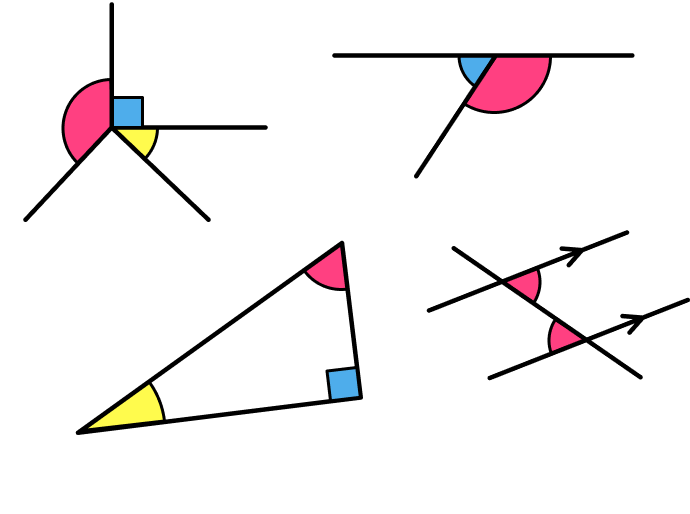
What are angles?
Angle rules
We can use angle rules to work out missing angles.
Angle rules are facts that we can apply to calculate missing angles in a diagram.
The five key angle facts that are used widely within the topic are:
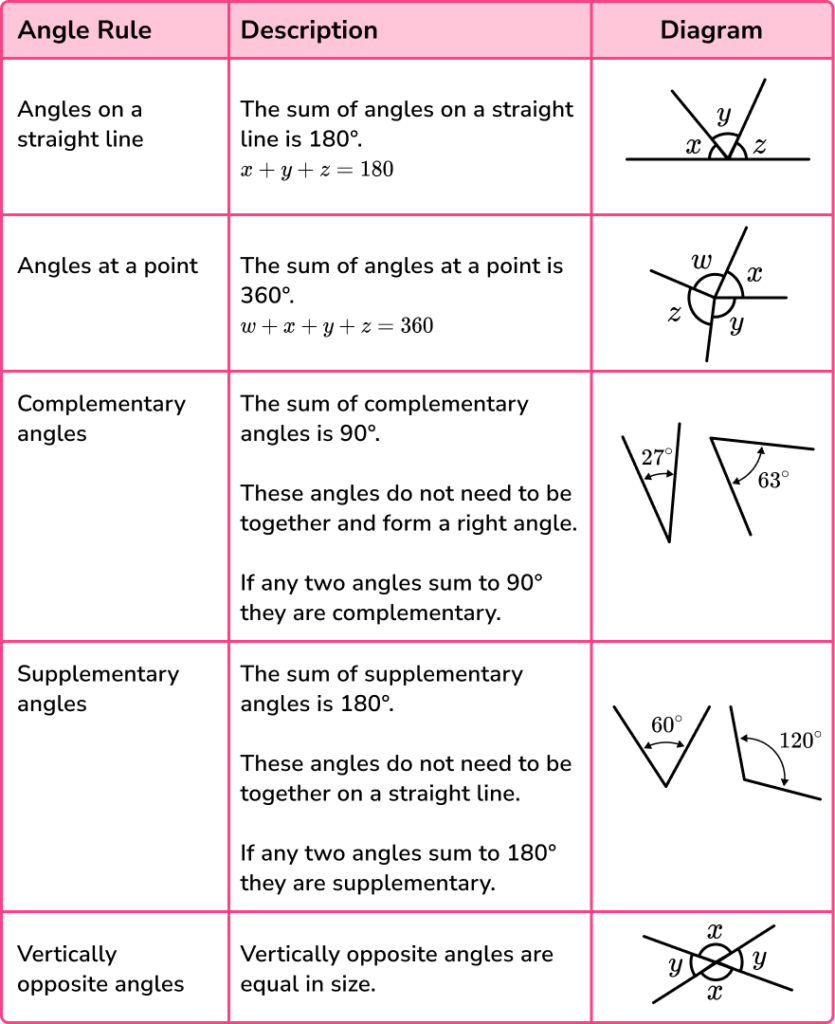
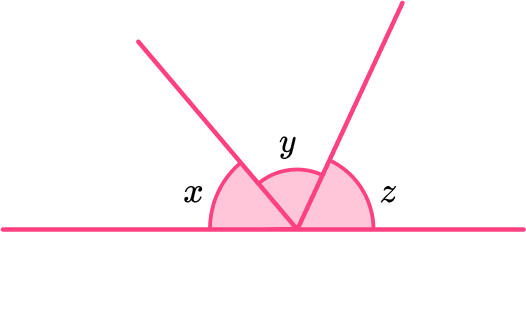
- Angles on a straight line
The sum of angles on a straight line is always equal to \bf{180^{o}.}
A straight line would be considered to be half of a full turn; if you were standing on the line facing towards one end, you would have to turn 180 degrees to face the other end of the line.
A straight line can be called a straight angle if there is a vertex on the line and the turn around that vertex is 180^{o}.
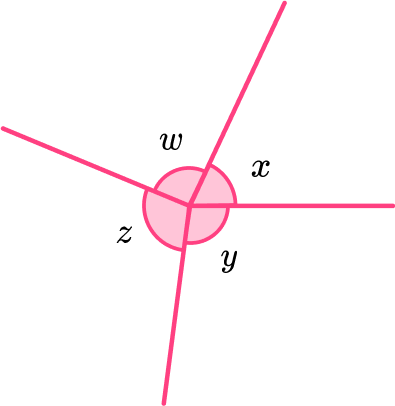
- Angles at a point
The sum of angles at a point is always equal to \bf{360^{o}} .
A point would be considered to be a full turn; if you were standing at the point facing in one direction, you would have to turn 360 degrees to return back to your original position.
- Complementary angles
The sum of complementary angles is always equal to \bf{90^{o}} .
Complementary angles therefore make up a right angle.
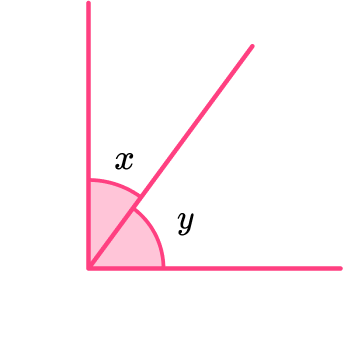
These angles do not need to be together and form a right angle. If any two angles sum to 90^o they are complementary.
- Supplementary angles
The sum of supplementary angles is always equal to \bf{180^{o}} .
Supplementary angles therefore make up a straight line.

These angles do not need to be together on a straight line. If any two angles sum to 180^o they are supplementary.
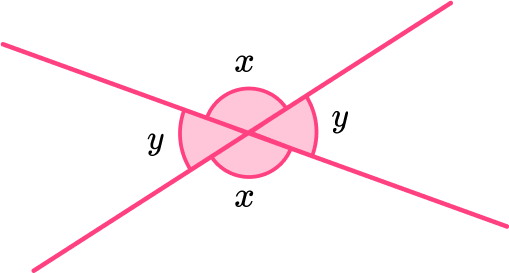
- Vertically opposite angles
Vertically opposite angles are equal.
This occurs when two straight lines meet (intersect) at a point known as a vertex, forming an x shape where the opposite pairs of angles are the same size. Also, two adjacent angles are supplementary (they add to equal 180^o ).
Step-by-step guide: Angle rules
Angles in polygons
We can calculate the interior and exterior angles of any polygon.
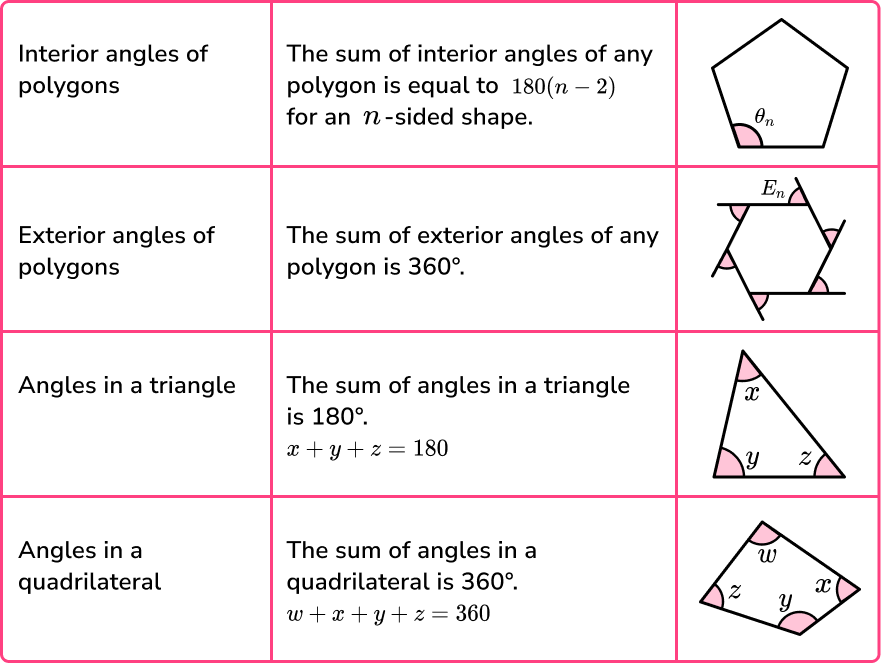
- Interior angles
The sum of interior angles in any n -sided shape is determined using the formula,
\text{Sum of interior angles}=180(n-2).One interior angle of a regular polygon with n -sides is determined using the formula,
\theta=\frac{180(n-2)}{n}.
For an irregular polygon, the missing angle is calculated by subtracting all of the known angles from the total sum of the interior angles of the polygon.
- Exterior angles
The sum of exterior angles for any polygon is \bf{360^{o}} .
Whereas the interior angle sum is different for each n -sided shape, the exterior angle sum is always 360^{o}, regardless of how many sides the polygon has.
This is because, as you walk around the perimeter of the shape, the exterior angle is the turn from the direction of one edge to the next edge of the polygon.
For a regular polygon, each exterior angle is equal to 360 divided by the number of sides, n, and so
\text{Exterior angle}=\frac{360}{n}.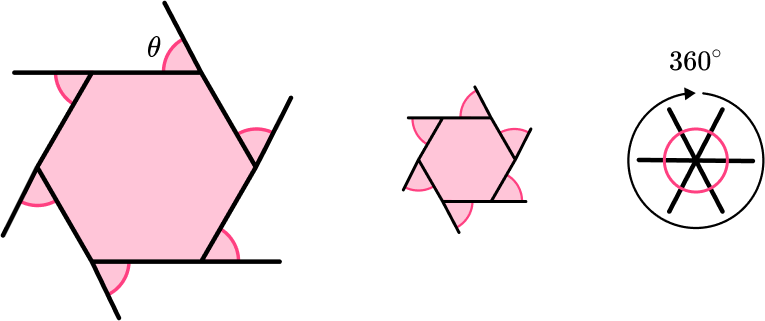
For an irregular polygon, the unknown exterior angle is calculated by subtracting the known exterior angles from 360^{o}.
The sum of an exterior angle and its adjacent interior angle is 180^{circ}, because they both lie on a straight line.
- Angles in a triangle
The sum of angles in a triangle is \bf{180^{o}} .
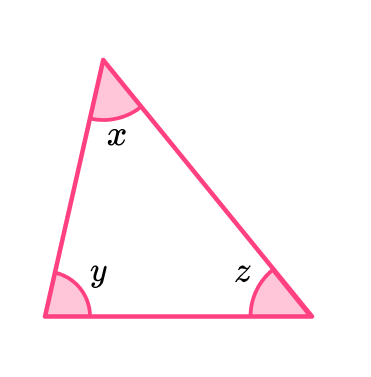
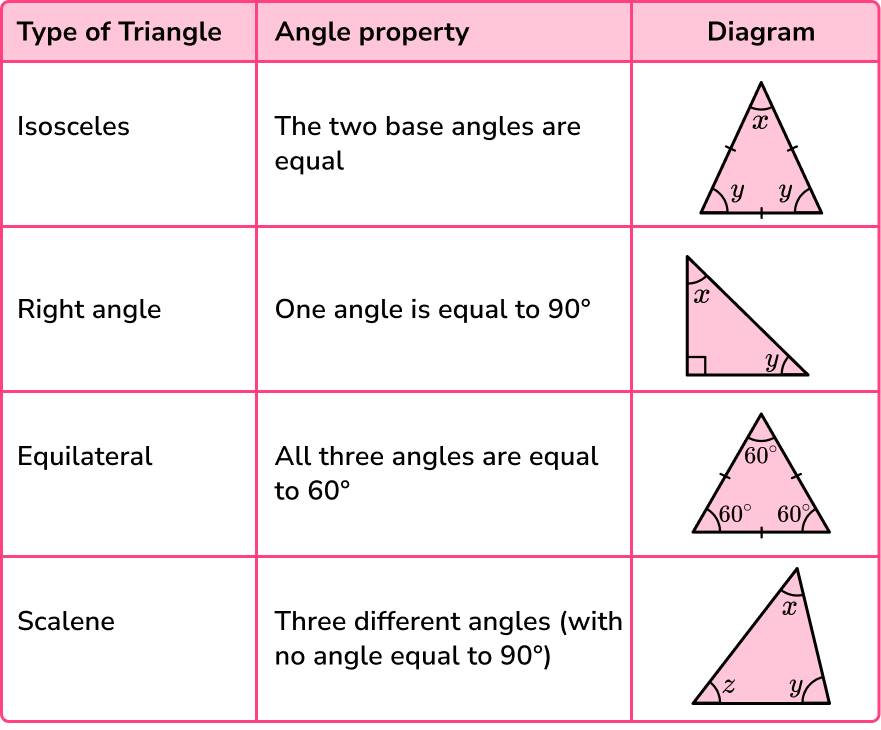
Remember that there are four different types of triangles, each with a specific angle property.
- Angles in a quadrilateral
The sum of angles in a quadrilateral is \bf{360^{o}} .
Any quadrilateral can be constructed from two adjacent triangles. This means that as the angle sum of a triangle is equal to 180^{o}, two triangles would have an angle sum of 360^{o}.
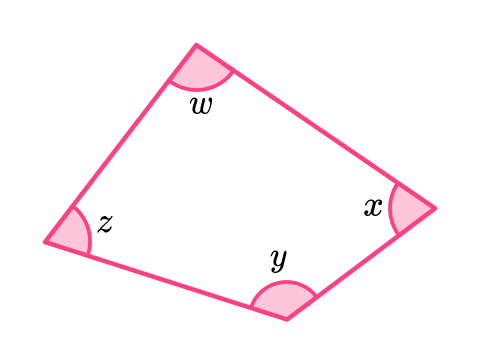
There are several different types of quadrilaterals, each with a specific angle property.
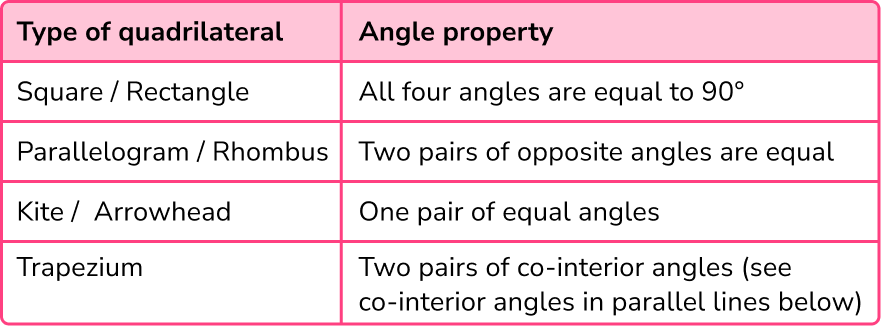
Step-by-step guide: Angle in polygons
Angles in parallel lines
Angles in parallel lines are facts that can be applied to calculate missing angles within a pair of parallel lines. The three key angle facts that are used when looking at angles in parallel lines are,
- Corresponding angles
- Alternate angles
- Co-interior angles

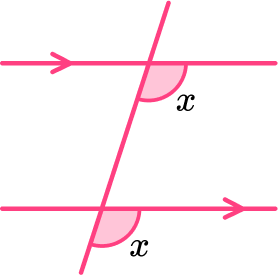
- Corresponding angles
Corresponding angles are equal.
When we intersect a pair of parallel lines with a transversal (another straight line), corresponding angles are the angles that occur on the same side of the transversal line. They are either both obtuse or both acute.
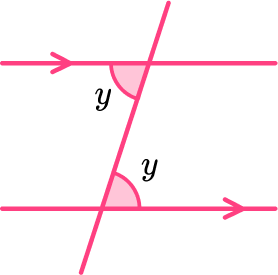
- Alternate angles
Alternate angles are equal.
When we intersect a pair of parallel lines with a transversal, alternate angles occur on opposite sides of the transversal line. They are either both obtuse or both acute.
- Co-interior angles
The sum of two co-interior angles is \bf{180^{o}} .
Co-interior angles occur in between two parallel lines when they are intersected by a transversal. The two angles that occur on the same side of the transversal always add up to 180^{o}.
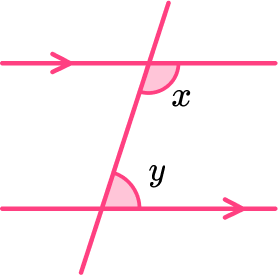
Step-by-step guide: Angles in parallel lines
How to use angles
We can use angles in lots of different contexts.
We will learn about,
- Types of angles
- Angle rules
- Angles in polygons
- Angles in parallel lines
Explain how to use angles

Angles worksheet
Get your free angles worksheet of 20+ questions and answers. Includes reasoning and applied questions.
COMING SOONAngles worksheet
Get your free angles worksheet of 20+ questions and answers. Includes reasoning and applied questions.
COMING SOONAngle rules examples
Example 1: angles on a straight line
Calculate the value of x.
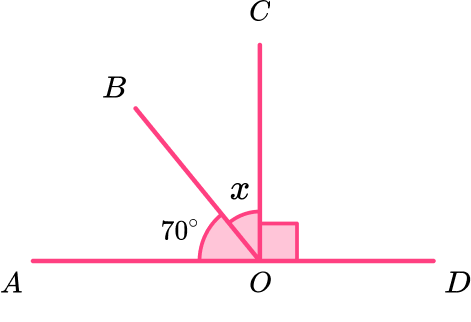
- Add all known angles.
The angle highlighted as a square is a right angle. A right angle measures 90^{o}. Adding the angles together, we can form the expression
70+90=160.2Subtract the angle sum from \bf{180^{o}} .
As the sum of angles on a straight line total 180^{o},
180-160=20.3Form and solve the equation.
Here we have no equation to solve as the missing angle is 20^{o}.
Example 2: angles at a point
Calculate the value of x.
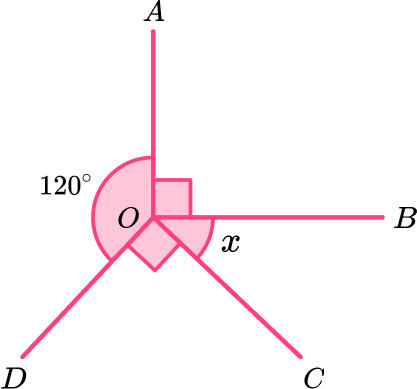
Add all known angles.
Subtract the angle sum from \bf{360^{o}} .
Form and solve the equation.
Here there is no equation to solve as we know the angle x=60^{o}.
Example 3: complementary angles
Angle AOB is complementary to BOC. Determine the size of the angle AOB.
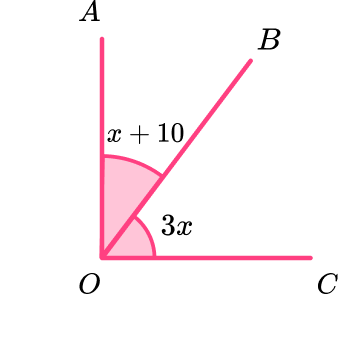
Identify which angles are complementary.
Here, the angles AOB and BOC are complementary.
Clearly identify which of the unknown angles the question is asking you to find the value of.
The question would like us to calculate the angle AOB.
Solve the problem and give reasons where applicable.
As the sum of the two angles is 90 degrees, forming an equation, we have
x+10+3x=90,
or
4x+10=90.
Solving this for x, we have
\begin{aligned} 4x&=90-10\\\\ 4x&=80\\\\ x&=20. \end{aligned}
Clearly state the answer using angle terminology.
We need to determine the size of angle AOB for the solution and so we need to substitute x=20 into x+10.
Angle AOB = x+10=20+10=30^{o}.
Example 4: supplementary angles
Given that AC is a straight line, determine the size of angle AOB.
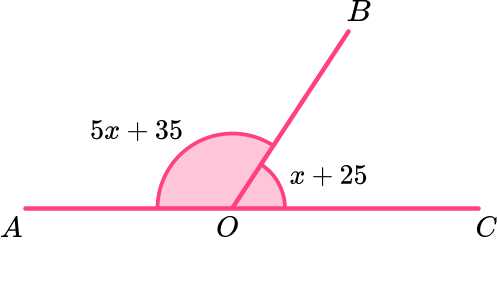
Identify which angles are supplementary.
As the line AC is a straight line, the two angles AOB and BOC are supplementary. This means that we can use the angle rule, “the sum of supplementary angles is 180^{o} ”.
Clearly identify which of the unknown angles the question is asking you to find the value of.
We need to determine the size of angle AOB.
Solve the problem and give reasons where applicable.
Adding the two angles 5x+35 and x+25 is equal to 180^{o}, which gives us the equation
5x+35+x+25=180.
Simplifying the left side of the equation, we have
6x+60=180.
Subtracting 60 from both sides of the equation, we have
6x=180-60=120.
Dividing both sides by 6, we have
x=120\div{6}=20.
Clearly state the answer using angle terminology.
We need to determine the size of angle AOB for the solution and so we need to substitute x=20 into angle AOB \ (5x+35).
Angle AOB = 5x+35=(5\times{20})+35=135^{o}.
Example 5: vertically opposite angles
Given that AC and BD are straight intersecting lines at the point O, determine the size of angle COD.
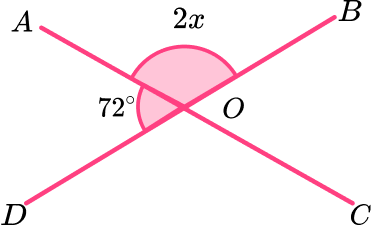
Identify which angles are vertically opposite to one another.
Angle COD is vertically opposite angle AOB and so angle COD = angle AOB.
Angle AOD is vertically opposite angle BOC and so angle AOD = angle BOC.
Clearly identify which of the unknown angles the question is asking you to find the value of.
We need to calculate the size of angle COD \ (2x).
Solve the problem and give reasons where applicable.
We need to inspect the lines and angles in the diagram to see what other rule(s) we need to apply.
As BD is a straight line, the two angles of 72^o and 2x are supplementary.
This means that if we use the rule “the sum of supplementary angles is 180^{o} ,” we can calculate the size of the angle 2x and hence the missing angle COD.
Forming an equation, we have
72+2x=180.
Subtracting 72 from both sides of the equation, and then dividing both sides by 2, we have
2x=180-72=108,
x=108\div{2}=54.
Clearly state the answer using angle terminology.
As x=54, \ 2x=2\times{x}=2\times{54}=108. As vertically opposite angles are equal,
Angle COD = 108^{o}.
Example 6: interior angles of a regular pentagon
What is the interior angle sum of a regular pentagon?
Identify how many sides the polygon has.
A pentagon has 5 sides.
Identify if the polygon is regular or irregular.
The polygon is regular.
If possible work out how many triangles could be created within the polygon by drawing lines from one vertex to all other vertices.

A regular pentagon contains 3 triangles.
Multiply the number of triangles by \bf{180} to calculate the sum of the interior angles.
State your findings.
The interior angle sum of a regular pentagon is 540^{o}.
Example 7: angles in a triangle
What type of triangle is ABC?
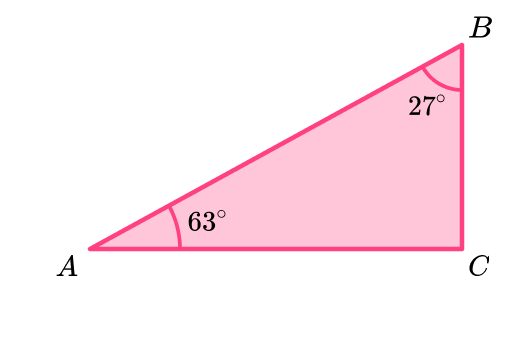
Add up the other angles within the triangle.
Subtract this total from \bf{180^{o}} .
The remaining angle is 90 degrees and so this is a right angle triangle.
Example 8: angles in a quadrilateral
ABCD is a kite. Calculate the size of angle ADO.
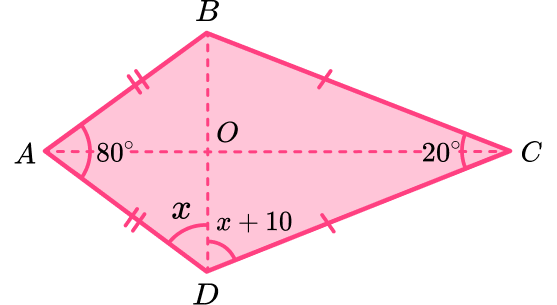
Use angle properties to determine any interior angles.
Angle ABC and ADC are equal as a kite has one pair of equal angles.
This means that ABC = ADC = 2x+10.
Updating the diagram with this information, we have
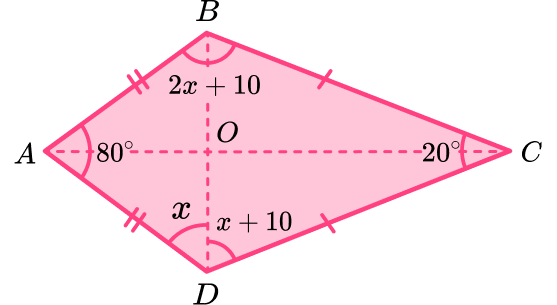
Add all known interior angles.
Subtract the angle sum from \bf{360^{o}} .
Form and solve the equation.
The remaining angles must therefore total 260^{o} and so we can form the equation
2x+10+2x+10=260.
Simplifying the left hand side of the equation, we have
4x+20=260.
Subtract 20 from both sides,
4x=260-20=240.
Divide both sides by 4,
x=240\div{4}=60.
ADO = 60^{o}.
Example 9: exterior angles
Calculate the exterior angle x for the hexagon below.
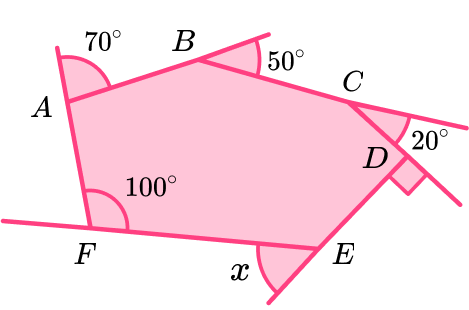
Identify the number of sides in any polygon given in the question.
This irregular hexagon has 6 sides.
Identify what the question is asking.
We need to find the value of the exterior angle, x.
Solve the problem using the information you have already gathered.
The known exterior angles of this hexagon are: 70^{o}, \ 50^{o}, \ 20^{o}, and 90^{o} (the right angle).
As the interior angle is supplementary to the exterior angle at F, the exterior angle at F is equal to 180-100 = 80^{o}.
We now have the known angles: 70^{o}, \ 50^{o}, \ 20^{o}, \ 90^{o}, \ 80^{o} and the unknown angle x.
Subtracting the known angles from 360, we have
x=360-(70+50+20+90+80)=360-310=50.
The missing exterior angle x=50^{o}.
Example 10: alternate angles
Calculate the size of the angle x.
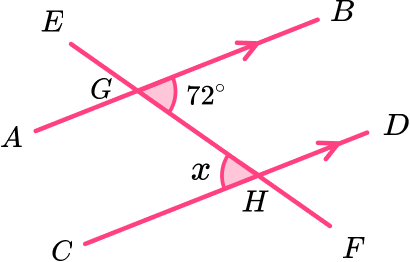
Highlight the angle(s) that you already know.
We know angle BGH and we want to find angle GHC.
State the alternate angle, co-interior angle or corresponding angle fact to find a missing angle in the diagram.
BGH is alternate to angle GHC (our unknown value x ), so we can state that x=72^{o}.
Use basic angle facts to calculate the missing angle.
This step isn’t required as the solution has been calculated.
x=72^{o}
Example 11: corresponding angles
Calculate the value of y.
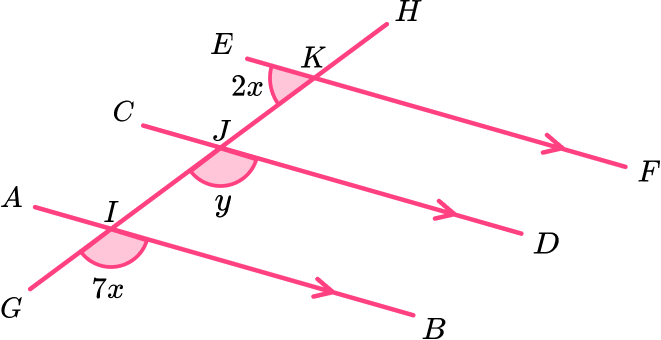
Highlight the angle(s) that you already know.
We do not know the numerical size of any angle in the diagram however we can use angles BIG, \ DJI and EKJ to determine the value of y.
The angle GIB is corresponding to GKF. As EF is a straight line we can calculate the value for x, which will help us to calculate the value of y.
State the alternate angle, co-interior angle or corresponding angle fact to find a missing angle in the diagram.
As GIB is corresponding to GKF, angle GKF = 7x.
Use basic angle facts to calculate the missing angle.
As EF is a straight line and the sum of angles on a straight line is 180, we can form the equation 2x+7x=180. Solving this equation we have
\begin{aligned} 9x&=180\\\\ x&=180\div{9}\\\\ x&=20 \end{aligned} .
As GKF = 7x, \ 7 \times 20=140 and so GKF = 140^{o}.
State the alternate angle, co-interior angle or corresponding angle fact to find a missing angle in the diagram.
Angle GKF is corresponding to GJD and so as corresponding angles are equal, GJD = 140^o and so
y=140^{o}.
Example 12: co-interior angles
Calculate the value of x.
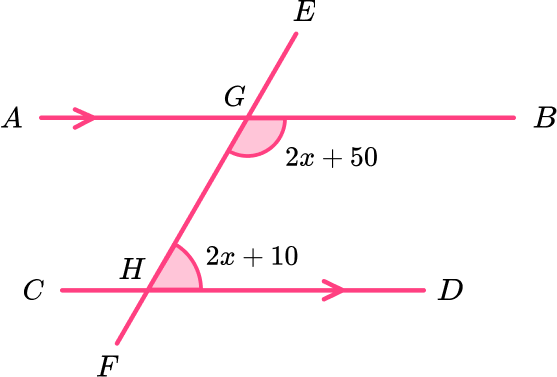
Highlight the angle(s) that you already know.
We know the two angles BGH and GHD.
State the alternate angle, co-interior angle or corresponding angle fact to find a missing angle in the diagram.
BGH is co-interior to GHD and so their angle sum is 180^{o}. Forming an equation for the two angles, we have
2x+50+2x+10=180.
Simplifying the left hand side of the equation, we have
4x+60=180.
Next, we subtract 60 from both sides
4x=180-60=120.
And finally divide by 4.
x=120\div{4}=30
x=30^{o}
Repeat this process until the required missing angle is calculated.
This step isn’t required as the solution has been calculated.
x=30^{o}
Common misconceptions
- Measuring angles with a protractor when the diagrams are not drawn accurately
When the question states that the diagram is not drawn accurately we cannot simply measure the missing angles using a protractor. We need to use angle facts to calculate the missing angle.
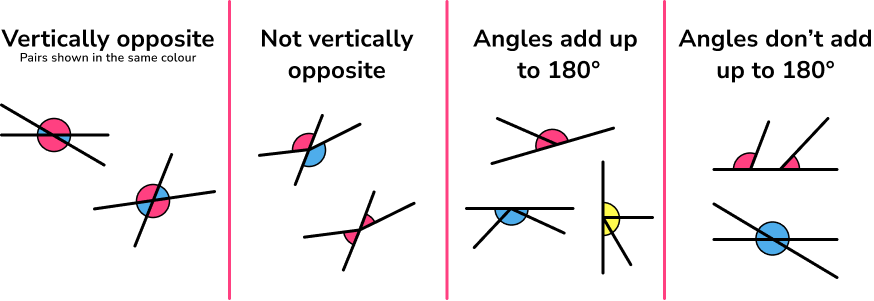
- Angles on a straight line and vertically opposite angle rules
With the straight line rule that only adjacent angles are considered, and for vertically opposite angles the lines must be straight.
- Exterior angles of a polygon
Exterior angles of a polygon have to travel in the same direction for the sum to be 360^{o}.

- Angles in triangles
Pairing up the incorrect angles in an isosceles triangle and using exterior angles when calculating the interior angle sum of a triangle.
Practice angles questions
1. Calculate the value of x.
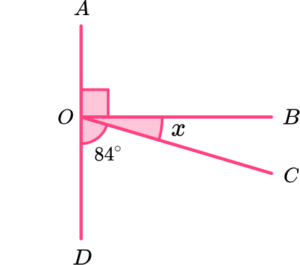




The sum of angles on a straight line is 180^{o}.
x=180-(90+84)=6^{o}
2. Calculate the value of x.
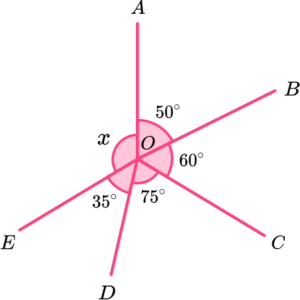




The sum of angles at a point is 360^{o}.
x=360-(50+60+75+35)=140^{o}
3. AOC is a right angle. Calculate the value of angle BOC.
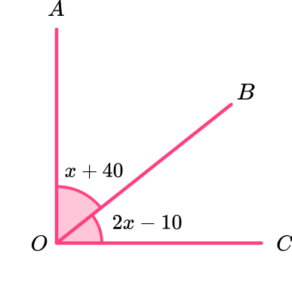




The sum of two complementary angles is 90^{o}.
\begin{aligned} x+40+2x-10&=90\\ 3x+30&=90\\ 3x&=60\\ x&=20 \end{aligned}
2x-10=2\times{20}-10=30^{o}.
4. AB is a straight line. Calculate the size of angle AOC.
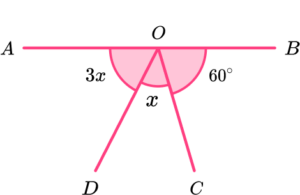




As AB is a straight line, angle AOC is supplementary to angle BOC.
Angle AOC = 3x+x=4x and so
4x=180-60=120
x=30^{o}.
5. The two straight lines AC and BD intersect at the point O. Calculate the value of x.
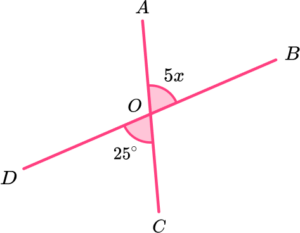




As AC and BD are straight lines, angle COD is vertically opposite angle AOB.
As vertically opposite angles are equal, we can form the equation
\begin{aligned} 5x&=25\\\\ x&=25\div{5}\\\\ x&=5. \end{aligned}
6. The hexagon below has two lines of symmetry. Calculate the size of the interior angle at A.
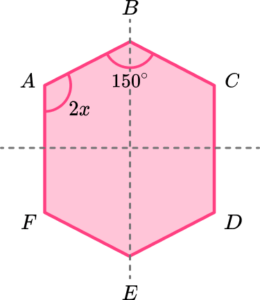




The interior angle at C = 2x given the vertical line of symmetry.
The interior angle at D,E, and F can be found using the horizontal line of symmetry: D = 2x, \ E = 150^{o}, and F = 2x.
The sum of angles in the hexagon is therefore
\begin{aligned} 2x+150+2x+2x+150+2x&=720\\\\ 8x+300&=720\\\\ 8x&=420\\\\ x&=52.5 \end{aligned}
As the interior angle at A is equal to 2x,
A =2x=2\times{x}=2\times{52.5}=105^{o}.
7. Calculate the value of y.
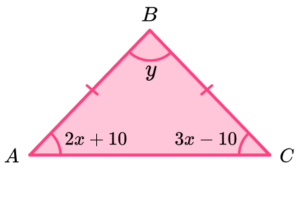




2x+10=2\times{20}+10=50
3x-10=3\times{20}-10=50
As the sum of angles in a triangle is 180^{o},
y=180-(50+50)=80^{o}.
8. Calculate the interior angle at A.
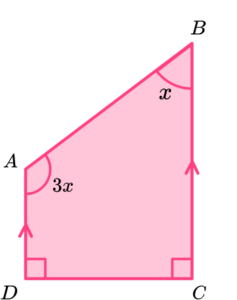




The sum of angles in a quadrilateral is 360^{o}.
\begin{aligned} 3x+x+90+90&=360\\\\ 4x+180&=360\\\\ 4x&=180\\\\ x&=45 \end{aligned}
3x=3\times{45}=105^{o}
9. Calculate the interior angle of a regular octagon.




1080\div{8}=135^{o}
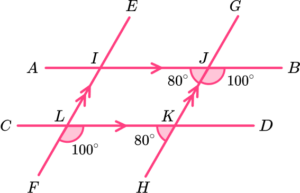
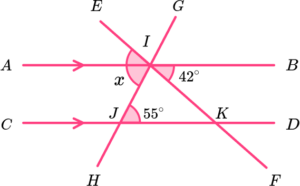
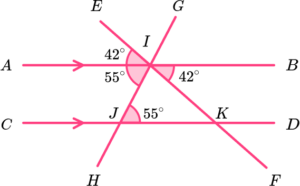
10. Which diagram only needs us to use alternate angles to determine the value of x?
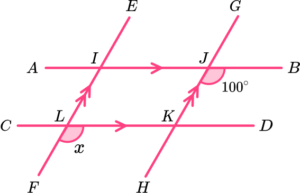

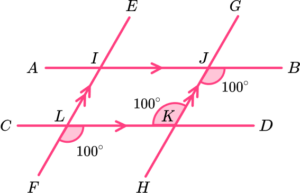



BJH is alternate to JKL.
JKL is alternate to KLF.
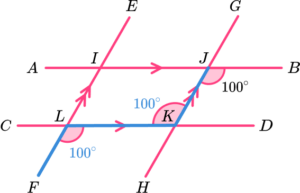
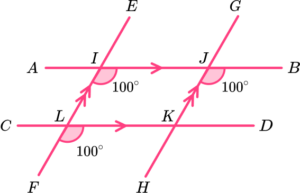
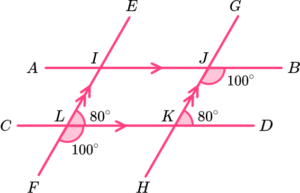
11. Which diagram needs us to use corresponding angles to determine the value of x?
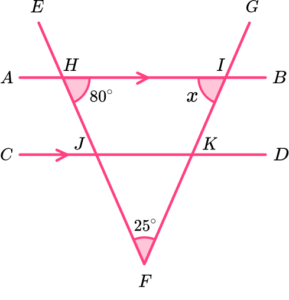


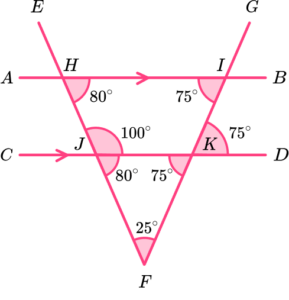

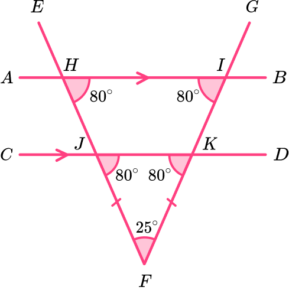

BJH is corresponding to KJF.
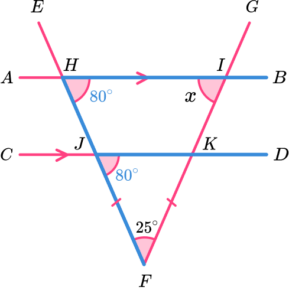
The sum of angles in a triangle is 180^o and so angle
JKF = 180-(80 + 25) = 75.
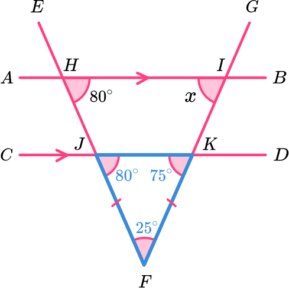
Angle JKL is corresponding to HIK.
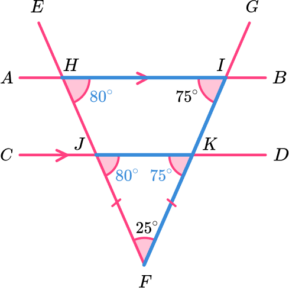
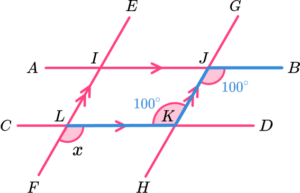
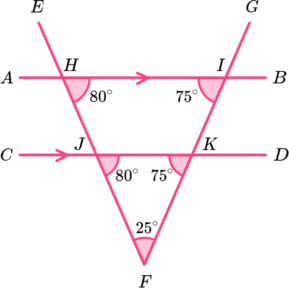
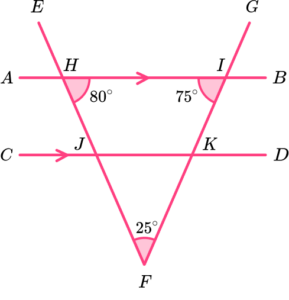
12. Which diagram uses co-interior angles to calculate the value of x?
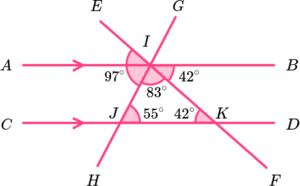


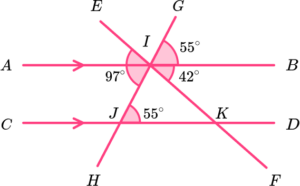

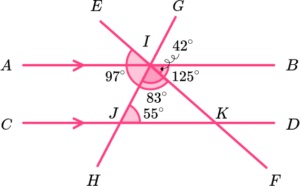

DJI is co-interior to BIJ.
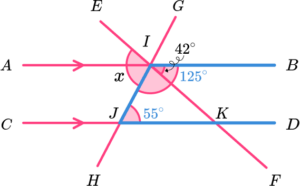
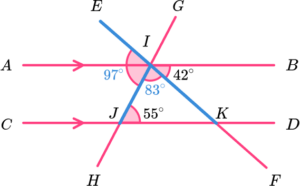
125-42 = 83.
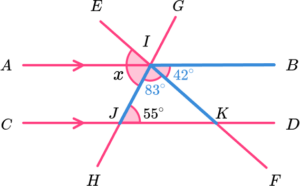
EF is a straight line. The sum of angles on a straight line is 180^{o}.
180-83 = 97^{o}.
Angles GCSE questions
1. A sock design requires four colours of thread. The pie chart below shows the proportion of each colour.

The ratio of white to yellow is 2:1. What fraction of the thread is white?
(4 marks)
(1)
240 \div (2+1)=80(1)
80 \times 2=160^o(1)
\frac{160}{360}(1)
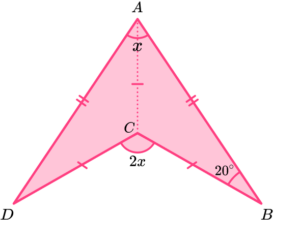
2. ABC and ACD are two congruent isosceles triangles.
Show that the angle BCD is double the angle BAD.
State any angle rules you use.
(5 marks)
BAC = ABC = 20^o and base angles in an isosceles triangle are equal.
(1)
ACB = 180-(20 + 20) = 140^o and the sum of angles in a triangle is 180^{o}.
(1)
ACD = ACB = 140^o and the two triangles are congruent.
(1)
BAD = 20 + 20 = 40^o and the two triangles are congruent.
(1)
BCD = 360-(140 + 140) = 80^o and the sum of angles at a point is 360^{o}.
(1)
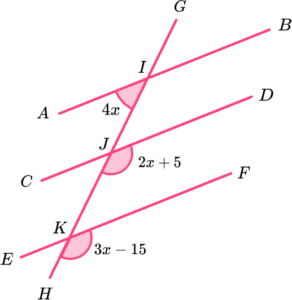
3. Below are the three lines AB, \ CD, and EF, intersected by the line GH.
Show that the lines AB, \ CD, and EF are not parallel.
(7 marks)
Method 1
If AB and CD are parallel, 4x+2x+5=180.
(1)
DJK is corresponding to BIJ.
(1)
The sum of angles on a straight line total 180^{o}.
(1)
x=29.1\dot{6}(1)
and
2x+5=3x-15(1)
x=20(1)
and
x must be the same for both equations.
(1)
Alternative Method
If AB and EF are parallel, 4x+3x-15=180.
(1)
FKH is corresponding to BIJ.
(1)
The sum of angles on a straight line total 180^{o}.
(1)
x=27.86 \ (2dp)(1)
and
2x+5=3x-15(1)
x=20(1)
and
x must be the same for both equations.
(1)
Learning checklist
You have now learned how to:
-
Recognise angles as a property of shape or a description of a turn
-
Apply the properties of angles at a point, angles at a point on a straight line, and vertically opposite angles
-
Derive and use the sum of angles in a triangle and use it to deduce the angle sum in any polygon, and to derive properties of regular polygons
-
Distinguish between regular and irregular polygons based on reasoning about equal sides and angles
-
Understand and use the relationship between parallel lines and alternate and corresponding angles
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.