Triangular prism

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

Learn more

In order to access this I need to be confident with:

3D shapes Area of a triangle Area of a rectangle Substituting into formulae

This topic is relevant for:

GCSE Maths Geometry and Measure 3D Shapes

Triangular Prism

Here we will learn about triangular prisms, including nets of triangular prisms and volume and surface area of triangular prisms.

There are also triangular prism worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What are triangular prisms?

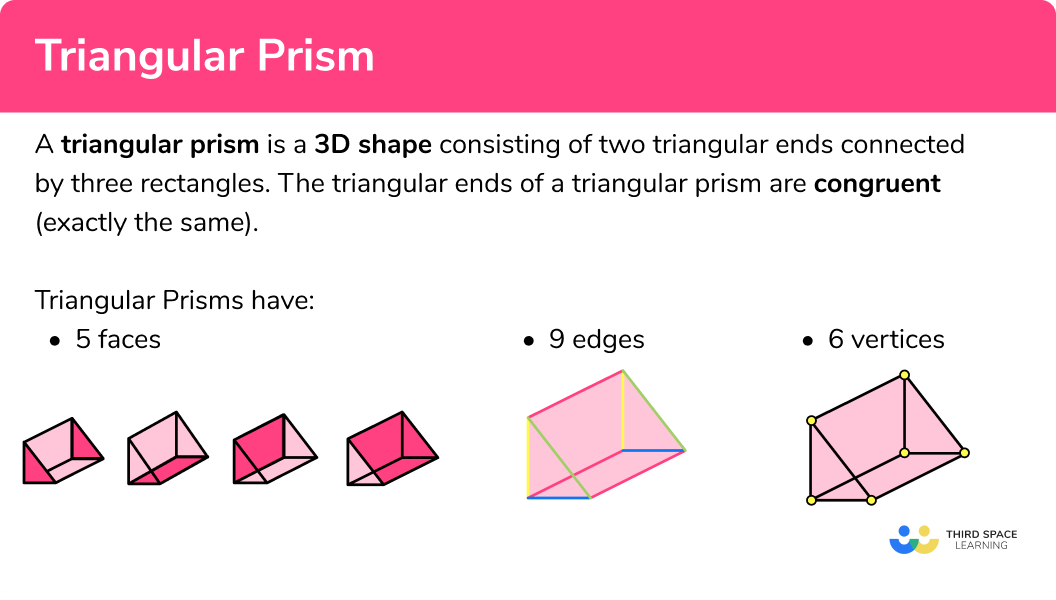
A triangular prism is a polyhedron (3D shape made from polygons) consisting of two triangular ends connected by three rectangles. The triangular ends of a triangular prism are congruent (exactly the same).

E.g.

Triangular Prism Image 1

Triangular Prism Image 2

What are triangular prisms?

Faces

A face of a 3D shape is a flat surface.

Triangular prisms have a total of $5$ faces – $2$ triangular faces and $3$ rectangular faces. The triangular faces of a triangular prism are congruent.

Edges

An edge of a 3D shape is a straight line between two faces.

Triangular prisms have $9$ edges:

Vertices

A vertex is a point where two or more edges meet.

Triangular prisms have $6$ vertices:

Nets

A net of a three-dimensional shape is the $2$ dimensional shape it would make if it were unfolded and laid flat. Nets can be folded up to make the 3D shapes.

Labelling a triangular prism

We can label the vertices (corners) of a prism to help us identify certain edges or faces.

E.g.

Using this labelling we can identify lengths,

E.g. the length AB:

We can also identify faces,

E.g. the face ABC:

Volume of a triangular prism

The volume of a triangular prism is how much space there is inside of the shape.

To calculate the volume of a triangular prism we find the area of the triangular cross-section and multiply it by the length of the prism (or height of the prism).

\text{Volume of a triangular prism } = \text{ Area of triangular cross section } \times \text{ length}

E.g.

Find the volume of the right triangular prism (so called because the triangular faces include a right angle.

\begin{array}{l} \text{Area of triangular cross-section:}\\\\ \text{Area }=\frac{1}{2}bh\\\\ \text{Area }=\frac{1}{2} \times 2 \times 4\\\\ \text{Area }=4\mathrm{cm}^{2}\\\\ \\ \text{Volume of triangular prism:}\\\\ \text{Volume }= \text{Area of triangular cross-section } \times \text{ length}\\\\ \text{Volume }=4 \times 7\\\\ \text{Volume }=28\mathrm{cm}^{3} \\\\ \end{array}

Volume is measured in cubic units (e.g. $mm^3, \ cm^3, \ m^3$ etc).

Step-by-step guide: Volume of a triangular prism

How to calculate the volume of a triangular prism

Calculate the area of the triangular cross-section.
Multiply the area by the length of the triangular prism.
Include the units.

Triangular Prism worksheet

Get your free triangular prism worksheet of 20+ questions and answers. Includes reasoning and applied questions.

COMING SOON

Triangular Prism worksheet

Get your free triangular prism worksheet of 20+ questions and answers. Includes reasoning and applied questions.

COMING SOON

Volume of a triangular prism example

Work out the volume of the triangular prism

Calculate the area of the triangular cross-section.

The base of the triangle is $10 \ cm$ .

The height of the triangle is $4 \ cm.$

The area formula for a triangle is:

\begin{array}{l} \text{Area of triangle }=\frac{1}{2} \times b \times h\\\\ \text{Area of triangle }=\frac{1}{2} \times 10 \times 4\\\\ \text{Area of triangle }=20 \end{array}

2Multiply the area by the length of the triangular prism.

The volume formula is:

\begin{aligned} &\text{Volume of triangular prism } = \text{ Area of triangular cross section } \times \text{ length} \\\\ &\text{Volume of triangular prism } = 20 \times 15 \\\\ &\text{Volume of triangular prism } = 300 \end{aligned}

3Include the units.

The measurements on this triangular prism are in $cm$ so the volume will be measured in $cm^3$ .

Volume $= 300 \ cm^3$

Surface area of a triangular prism

The surface area of a triangular prism is the total area of all of the faces.

To work out the surface area of a triangular prism, we need to work out the area of each face and add them all together.

Lateral faces are all of the faces of an object excluding the top and the base. For a triangular prism the top and the base are triangles and the lateral faces are rectangular sides. The lateral surface area is the total area of the rectangular sides

The triangular faces of a triangular prism are congruent (exactly the same) but, unless the triangle is an isosceles triangle or an equilateral triangle, the rectangles are all different.

E.g.

\begin{aligned} &\text{Face} \quad \quad \quad \quad \quad \quad \quad \quad \text{Area} \\\\ &\text{Front} \quad \quad \quad \quad \quad \quad \frac{1}{2} \times 6 \times 8 = 24 \\\\ &\text{Back} \quad \quad \quad \quad \quad \quad \quad \quad \; 24 \\\\ &\text{Bottom} \quad \quad \quad \quad \quad \quad 6 \times 5=30\\\\ &\text{Left side} \quad \quad \quad \quad \quad \; 8 \times 5=40\\\\ &\text{Right side} \quad \quad \quad \quad \;\;\; 10 \times 5=50 \end{aligned}

Total surface area $=168\; cm^2$

Since it is an area, surface area is measured in square units (e.g. $mm^2, \ cm^2, \ m^2$ etc).

Step-by-step guide: Surface area of a triangular prism

How to calculate the surface area of a triangular prism

Work out the area of each face.
Add the five areas together.
Include the units.

How to calculate the surface area of a triangular prism

Surface area of a triangular prism example

Work out the surface area of the triangular prism

Work out the area of each face.

\begin{aligned} &\text{Face} \quad \quad \quad \quad \quad \quad \quad \quad \text{Area} \\\\ &\text{Front} \quad \quad \quad \quad \quad \quad \frac{1}{2} \times 6 \times 8 = 24 \\\\ &\text{Back} \quad \quad \quad \quad \quad \quad \quad \quad \; 24 \\\\ &\text{Bottom} \quad \quad \quad \quad \quad \quad 4 \times 6=24\\\\ &\text{Left side} \quad \quad \quad \quad \quad \; 4 \times 8=32\\\\ &\text{Right side} \quad \quad \quad \quad \;\;\; 4 \times 10=40 \end{aligned}

2 Add the five areas together.

24+24+24+32+40=144

3Include the units.

The measurements on the triangular prism are in mm therefore the total surface area of the triangular prism $= 144mm^2$ .

Common misconceptions

Missing/incorrect units

You should always include units in your answer.
Volume is measured in units cubed (e.g. $mm^3, \ cm^3, \ m^3$ etc).
Surface area is measured in units squared (e.g. $mm^2, \ cm^2, \ m^2$ etc)

Calculating with different units

You need to make sure all measurements are in the same units before calculating volume.
E.g. You can’t have some measurements in $cm$ and some in $m$

Using the wrong formula

Be careful to apply the correct prism related formula to the correct question type.

Calculating volume instead of surface area

Volume and surface area are different things – volume tells us the space within the shape whereas surface area is the total area of the faces. To find surface area, work out the area of each face and add them together

Using the wrong measurements to work out the area of the triangle faces

In surface area questions, we need to know all three side lengths of the triangle however we only need the base and the height to calculate the area of the triangle.

Practice triangular prism questions

52 \mathrm{cm}^{3}

144 \mathrm{cm}^{3}

72 \mathrm{cm}^{3}

720 \mathrm{cm}^{3}

\begin{aligned} \text{Area of triangle }&=\frac{1}{2} \times 2 \times 9\\\\ &=9 \end{aligned}

\begin{aligned} \text{Volume of triangular prism }&=9 \times 8\\\\ &=72\mathrm{cm}^{3} \end{aligned}

330 \mathrm{mm}^{3}

3.3 \mathrm{mm}^{3}

3300 \mathrm{mm}^{3}

122.6 \mathrm{mm}^{3}

Notice that we have measurements in $mm$ and $cm.$ We can convert the measurements in $cm$ to $mm.$

1cm = 10mm, 1.1cm = 11mm

Now we can work out the volume:

\begin{aligned} \text{Area of triangle }&=\frac{1}{2} \times 10 \times 11\\\\ &=55 \end{aligned}

\begin{aligned} \text{Volume of triangular prism }&=55 \times 6\\\\ &=330 \mathrm{mm}^{3} \end{aligned}

32cm

16cm

3cm

6cm

\begin{aligned} \text{Area of triangle }&=\frac{1}{2} \times 4 \times h\\\\ &=2h \end{aligned}

\begin{aligned} \text{Volume of triangular prism }&=2h \times 8\\\\ 96 &= 16h\\\\ 6&=h \end{aligned}

The height is $6cm.$

312 \mathrm{m}^{2}

438 \mathrm{m}^{2}

360 \mathrm{m}^{2}

408 \mathrm{m}^{2}

Work out the area of each face:

\begin{aligned} &\text{Face} \quad \quad \quad \quad \quad \quad \quad \quad \text{Area} \\\\ &\text{Front} \quad \quad \quad \quad \quad \quad \frac{1}{2} \times 8 \times 6 = 24 \\\\ &\text{Back} \quad \quad \quad \quad \quad \quad \quad \quad \; 24 \\\\ &\text{Bottom} \quad \quad \quad \quad \quad \quad 13 \times 8=104\\\\ &\text{Left side} \quad \quad \quad \quad \quad \; 13 \times 6=78\\\\ &\text{Right side} \quad \quad \quad \quad \;\;\; 13 \times 10=130 \end{aligned}

\text{Total surface area }=24+24+104+78+130=360\mathrm{m}^{2}

112.5 \mathrm{cm}^{2}

178.9 \mathrm{cm}^{2}

160 \mathrm{cm}^{2}

216.7 \mathrm{cm}^{2}

Work out the area of each face:

\begin{aligned} &\text{Face} \quad \quad \quad \quad \quad \quad \quad \quad \text{Area} \\\\ &\text{Front} \quad \quad \quad \quad \quad \quad \frac{1}{2} \times 5 \times 5 = 12.5 \\\\ &\text{Back} \quad \quad \quad \quad \quad \quad \quad \quad \; 12.5 \\\\ &\text{Bottom} \quad \quad \quad \quad \quad \quad 9 \times 7.1=63.9\\\\ &\text{Left side} \quad \quad \quad \quad \quad \; 9 \times 5=45\\\\ &\text{Right side} \quad \quad \quad \quad \;\;\; 9 \times 5=45 \end{aligned}

\text{Total surface area }=12.5+12.5+63.9+45+45=178.9\mathrm{cm}^{2}

157500 \mathrm{cm}^{2}

2346.75 \mathrm{cm}^{2}

26775 \mathrm{cm}^{2}

33375 \mathrm{cm}^{2}

Notice that we have measurements in $cm$ and $m.$ We have been asked for the answer in $cm^2$ so we need to convert $m$ to $cm:$
$1.5m=150cm.$

Now we can work out the area of each face:

\begin{aligned} &\text{Face} \quad \quad \quad \quad \quad \quad \quad \quad \text{Area} \\\\ &\text{Front} \quad \quad \quad \quad \quad \quad \frac{1}{2} \times 60 \times 35 = 1050 \\\\ &\text{Back} \quad \quad \quad \quad \quad \quad \quad \quad \; 1050 \\\\ &\text{Bottom} \quad \quad \quad \quad \quad \quad 150 \times 60=9000\\\\ &\text{Left side} \quad \quad \quad \quad \quad \; 150 \times 35=5250\\\\ &\text{Right side} \quad \quad \quad \quad \;\;\; 150 \times 69.5=10425 \end{aligned}

\text{Total surface area }=1050+1050+9000+5250+10425=26775\mathrm{cm}^{2}

Triangular prisms GCSE questions

1. Work out the volume of the triangular prism

Triangular Prism GCSE Question 1

(2 marks)

Show answer

\text{Area of triangle: } \frac{1}{2} \times 14 \times 10=70

(1)

\text{Volume of triangular prism: } 70 \times 20 = 1400 \mathrm{mm}^{3}

(1)

2. (a) Which of these is a net of a triangular prism?

Triangular Prism GCSE Question 2 Image 1

Triangular Prism GCSE Question 2 Image 3

(b) What would the surface area of the triangular prism be?

(3 marks)

Show answer

(a) A

(1)

(b)

\text{Triangles: } \frac{1}{2} \times 3 \times 4 = 6 \mathrm{cm}^{2}

(1)

\text{Rectangles: } 12 \times 5 =60, 12 \times 4 = 48, 12 \times 3 = 36

(1)

\text{Surface area: }6+6+60+48+36=156\mathrm{cm}^{2}

(1)

3. This triangular prism has a volume of $300cm^3.$ Work out the surface area of the prism.

Triangular Prism GCSE Question 3

(5 marks)

Show answer

\text{Area of triangle: } \frac{1}{2} \times 5 \times 12 = 30 \mathrm{cm}^{2}

(1)

300=30 \times \text{length}

(1)

\text{length } =10cm

(1)

\text{Surface area }= 30+30+50+120+130

(1)

\text{Surface area }=360\mathrm{cm}^{2}

(1)

Learning checklist

You have now learned how to:

Recognise a triangular prism

Calculate the volume of a triangular prism

Calculate the surface area of a triangular prism

Apply formulae to calculate and solve problems involving triangular prisms

Use the properties of faces, surfaces, edges and vertices to solve problems in 3-D

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.