Prism shape

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

Learn more

In order to access this I need to be confident with:

3D shapes Area of triangles and quadrilaterals Substituting into formulae

This topic is relevant for:

GCSE Maths Geometry and Measure 3D Shapes

Prism Shape

Here we will learn about prisms, including what prisms are, types of prisms, nets of prisms and how to find the volume and surface area of prisms.

There are also volume and surface area of prisms worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is a prism shape?

A prism shape is a polyhedron (a 3D shape made from polygons) with a constant cross section through one dimension. A prism shape has two congruent faces (identical ends).

For example, below are three different types of prisms:

The name of the prism is represented by the shape of its cross section.

Faces, edges and vertices

A prism can be characterised using three features: faces, vertices and edges:

Face: a closed, flat surface surrounded by edges and vertices.
Edge: connects two vertices with a straight line
Vertex (pl. vertices): a point where two or more edges meet.

We can label the vertices (corners) of a prism to help us identify certain edges or faces. Below is an example of a triangular prism where the letters $A$ – $F$ represent the $6$ vertices of the prism:

Using this labelling we can identify lengths such as the length $AB$ :

We can also identify faces such as the face $ABC$ :

The number of faces, edges and vertices can vary depending on the prism. Let’s look at some examples:

Shape	Faces	Edges	Vertices
Triangular prism	5	9	6
Cuboid (rectangular prism)	6	12	8
Pentagonal prism	7	15	10
L-shaped prism	8	18	12

A prism is irregular if the cross section is not a regular polygon. For example, the L-shaped prism above is an irregular prism because the cross section is not a regular polygon.

What is a prism?

Nets

If you unfold a three-dimensional shape and lay it down so that it is flat, the result would be the net of the shape. We can draw a net for any prism.

E.g.

Volume of a prism

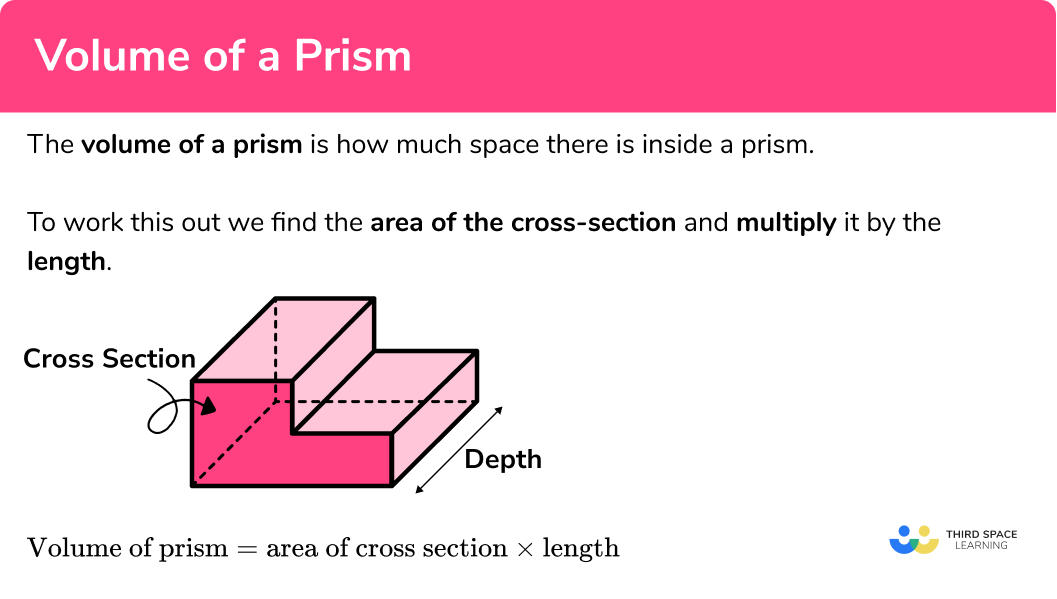
The volume of a prism is how much space there is inside a prism.

To calculate the volume of a prism, we find the area of the cross section and multiply it by the depth.

Volume of prism = Area of cross section × Depth

Volume is measured in cubic units (e.g. $mm^3, cm^3, m^3$ etc).

Step-by-step guide: Volume of a prism

Volume of a prism

How to calculate the volume of a prism

In order to do this I need to follow the steps:

Write down the formula.
Calculate the area of the cross section.
Calculate the volume of the prism.
Write the answer, including the units.

How to calculate the volume of a prism

Prism shape worksheet

Get your free prism shape worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Prism shape worksheet

Get your free prism shape worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Volume of a prism examples

Example 1: triangular prism, given the area of the cross-section

Below is a triangular prism:

The cross-sectional area of the prism is $43cm^2$ . Calculate the volume of the prism.

Write down the formula.

Volume of prism = Area of cross section × Depth

2Calculate the area of the cross section.

The area of the cross section is already stated as $43cm^2$ so we can move on to the next step.

3Calculate the volume of the prism.

\[\text{Volume of prism }=\text{Area of cross section }\times\text{Depth}\\ =43\times{9}\\ =387\]

4Write the answer, including the units.

The measurements on this prism are in cm so the volume will be measured in $cm^3$ .

Volume = $387cm^3$ .

Example 2: parallelogram prism

Work out the volume of the prism

Write down the formula.

Volume of prism = Area of cross section × Depth

2Calculate the area of the cross section.

\[\text{Area of a parallelogram }=b\times{h}\\ =8\times{3}\\ =24\]

3Calculate the volume of the prism.

\[\text{Volume of prism }=\text{Area of cross section }\times{Depth}\\ =24\times{20}\\ =480\]

4Write the answer, including the units.

The measurements on this prism are in m so the volume will be measured in $m^3$ .

Volume = $480m^3$ .

Example 3: trapezoidal prism

Calculate the volume of the prism below.

Write down the formula.

Volume of prism = Area of cross section × Depth

2Calculate the area of the cross section.

\[\text{Area of cross section (trapezium) }=\frac{1}{2}(a+b)h\\ =\frac{1}{2}(5+9)\times{4}\\ =28\text{cm}^{2}\]

3Calculate the volume of the prism.

\[\text{Volume of prism }=\text{Area of cross section }\times\text{Depth}\\ =28\times{10}\\ =280\]

4Write the answer, including the units.

Volume = $280cm^3$

Surface area of a prism

The surface area of a prism is the total area of all of the faces.

The surface area of a prism is special because all of the lateral faces are rectangles. To calculate the surface area of a prism, we calculate twice the area of the cross section and add the perimeter of the cross section multiplied by the depth of the prism.

In general, the surface area of any prism is:

Surface Area of a Prism = $2A+PD$

where:

$A$ = Area of the cross section
$P$ = Perimeter of the cross section
$D$ = Depth of the prism

Step-by-step guide: Surface area of a prism

Surface area of a prism

How to calculate the surface area of a prism

In order to work out the surface area of a prism:

Calculate the area of the cross section.
Calculate the perimeter of the cross section.
Substitute all known values into the formula and solve.
Write the answer, including the units.

How to calculate the surface area of a prism

Surface area of a prism examples

Example 4: surface area using a formula

Calculate the surface area of the following triangular prism.

Calculate the area of the cross section.

The cross section is a right angle triangle.

\[A=\frac{1}{2}(b\times{h})\\ =\frac{1}{2}(5\times{12})\\ =30\text{cm}^{2}\]

2Calculate the perimeter of the cross section.

The perimeter is the sum of the edges of the cross section:

P=5+12+13=30\text{cm}

3Substitute all known values into the formula and solve.

Using the formula Surface Area of a Prism = $2A+PD$ , when $A=30, P=30,$ and $D=10$ , we have

\[\text{SA}=2\times{30}+(30\times{10})\\ =60+300\\ =360.\]

4Write the answer, including the units.

The surface area of the triangular prism is $360cm^2$ .

Example 5: surface area of a cylinder

A cylinder has a height of $5m$ and a radius of $2m$ . Calculate the surface area of the cylinder. Write your answer in terms of $\pi$ .

Calculate the area of the cross section.

The cross section is a circle.

\[A=\pi\times{r}^{2}\\ =\pi\times{2}^{2}\\ =4\pi\text{ m}^{2}\]

2Calculate the perimeter of the cross section.

The perimeter of a circle is the circumference:

P=\pi\times{2r}=\pi\times{2}\times{2}=4\pi\text{ m}

3Substitute all known values into the formula and solve.

Using the formula Surface Area of a Prism = $2A+PD$ , when $A=4, P=4,$ and $D=5$ , we have

\[\text{SA}=2\times{4\pi}+(4\pi\times{5})\\ =8\pi+20\pi\\ =28\pi.\]

4Write the answer, including the units.

The surface area of the triangular prism is $28\pi\text{ m}^{2}$

Example 6: surface area of a compound prism

Calculate the surface area of the compound prism below.

Calculate the area of the cross section.

The cross section is a kite.

\[A=\frac{1}{2}(w\times{h})\\ =\frac{1}{2}(16\times{21})\\ =168\text{cm}^{2}\]

2Calculate the perimeter of the cross section.

The perimeter is the sum of the edges of the cross section:

P=10+17+17+10=54\text{cm}

3Substitute all known values into the formula and solve.

Using the formula Surface Area of a Prism = $2A+PD$ , when $A=168, P=54,$ and $D=4,$ we have

\[\text{SA}=2\times{168}+(54\times{4})\\ =336+216\\ =552.\]

4Write the answer, including the units.

The surface area of the compound prism is $552cm^2$ .

Common misconceptions

Calculating the volume instead of the surface area of the prism

Volume and surface area are different things – volume tells us the space within the shape whereas surface area is the total area of the faces. To find surface area, work out the area of each face and add them together.

All of the rectangles have the same area

Usually all of the rectangles have different areas (unless the shape of the cross section is a regular polygon)

Missing faces

This usually occurs on a compound prism where it can be difficult to visualise all of the face

Missing/incorrect units

You should always include units in your answer. Remember, volume is measured in units cubed (e.g. $mm^3, cm^3, m^3$ etc) and surface area is measured in units squared (e.g. $mm^2, cm^2, m^2$ etc)

Calculating with different units

You need to make sure all measurements are in the same units before calculating volume or surface area. (E.g. you can’t have some in $cm$ and some in $m$ )

Using the wrong formula

Be careful to apply the correct prism related formula to the correct question type.

Practice prism shape questions

160cm^3

90cm^3

72cm^3

144cm^3

\text{Area of trapezium }=\frac{1}{2}(3+5)\times{4}\\ =16

\text{Volume of prism }=16\times{9}\\ =144\mathrm{cm}^{3}

630cm^3

990cm^3

526cm^3

17820cm^3

Area of cross section:
$6 \times 5=30\\ 3\times 11=33\\ 30+33=63$

\text{Volume of prism }=63 \times 10\\ =630\mathrm{cm}^{3}

16200m

8m

0.178m

6m

We know the area of the octagon is $45m^2$ and the volume of the prism is $360m^3$ .

\text{Volume of prism } = \text{Area of cross-section } \times \text{Depth}\\ 360=45 \times{D}\\ D=8

The depth of the prism is $8m$ .

1056m^2

800m^2

960m^2

776m^2

Work out the area of each face:

Face	Area
Front	12×4=48
Back	48
Bottom	12×20=240
Top	240
Left side	5×20=100
Right side	100

\text{Total surface area }=48+48+240+240+100+100=776\mathrm{m}^{2}

252000cm^2

28200cm^2

4440cm^2

6600cm^2

1.2m=120cm

Face	Area
Front	70×30=2100
Back	2100
Bottom	70×120=8400
Top	8400
Left side	30×120=3600
Right side	3600

\text{Total surface area }=2100+2100+8400+8400+3600+3600=28200\mathrm{cm}^{2}

484mm^2

398mm^2

374mm^2

286mm^2

Area of cross section:
Area A: $\frac{1}{2} \times 8 \times 3=12$
Area B: $4\times 8=32$
Total area = $12+32=44$

Work out the area of each face:

Face	Area
Front	44
Back	44
Bottom	8×11=88
Left side	4×11=44
Top left	5×11=55
Top right	55
Right side	44

\text{Total surface area }=44+44+88+44+55+55+44=374\mathrm{mm}^{2}

Prism shape GCSE questions

1. Work out the surface area of the prism

(3 marks)

Show answer

$\frac{1}{2}(7+17) \times 12=144$
For calculating the area of the cross section (trapezium)

(1)

$272, 208, 208$ and $112$
For calculating the area of each lateral face (rectangles)

(1)

$144+144+272+208+208+112=1088\mathrm{cm}^{2}$
For calculating the total surface area of the prism

(1)

2. (a) The volume of this prism is $132m^3$ . Work out the height of the prism.

(b) Hence calculate the surface area of the prism.

Show answer

(a)
$5h$
For calculating the area of the cross section

(1)

$5h\times 12=60h$
For calculating the volume of the prism

(1)

$60h=132$
For forming an equation to calculate the height of the prism

(1)

$h=132\div{60}=2.2\text{m}$
For the correct answer

(1)

(b)
$5 \times 2.2=11$
For calculating the area of the cross section

(1)

$60(T), 60(B), 36(L), 36(R)$
For calculating the area of the rectangular faces

(1)

$\text{Total surface area: }11+11+60+60+36+36=214\mathrm{m}^{2}$
For calculating the total surface area of the prism

(1)

3. Richard would like to fill the container below with apple juice.

Can Richard pour $5$ litres of apple juice into the container without it overflowing?

(4 marks)

Show answer

$\frac{1}{2} (12+16) \times 12=168$
For calculating the area of the cross section (trapezium)

(1)

$168 \times 25 = 4200\mathrm{cm}^{3}$
For calculating the volume of the container

(1)

$4200\mathrm{cm}^{3}=4.2\text{ litres}$
For converting the volume into litres

(1)

No, it will not fit
For correct conclusion

(1)

Learning checklist

You have now learned how to:

Derive and apply formulae to calculate and solve problems involving prisms

Use the properties of faces, surfaces, edges and vertices of prisms to solve problems in 3-D

Calculate surface areas and volumes of composite solids

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.