Volume of a cuboid

GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

Teacher-trusted tutoring

In order to access this I need to be confident with:

3D shapes Area of a rectangle Substituting into formulae Decimals

This topic is relevant for:

GCSE Maths Geometry and Measure 3D Shapes Cuboid

Volume Of A Cuboid

Here we will learn about the volume of a cuboid, including how to calculate the volume of a cuboid and how to find missing lengths of a cuboid given its volume.

There are also volume and surface area of a cuboid worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

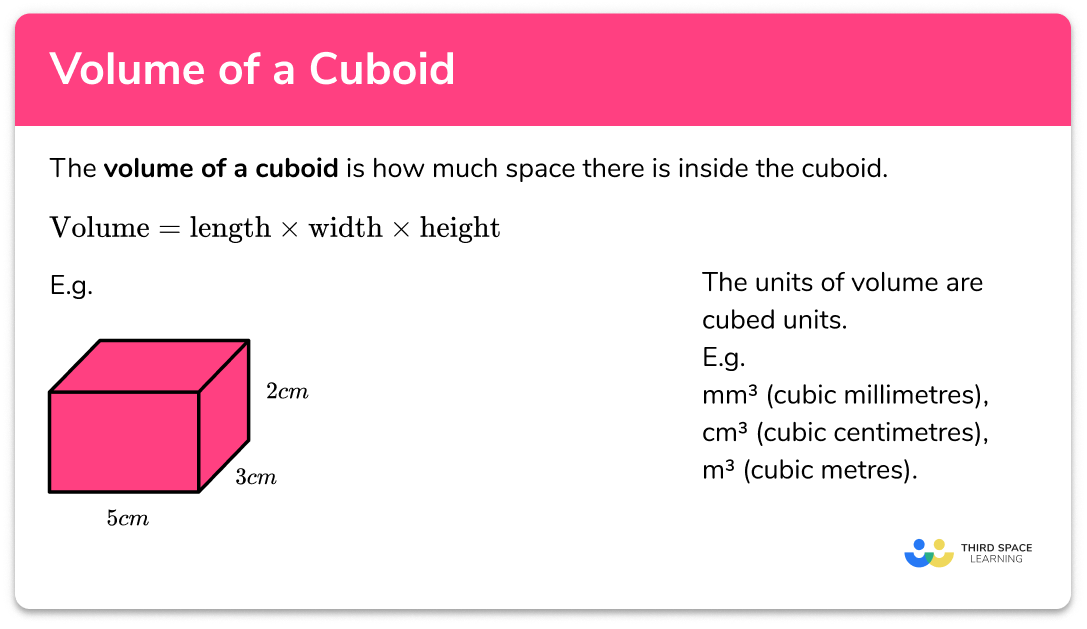
What is volume of a cuboid?

The volume of a cuboid is the amount of space there is within a cuboid.

Cuboids are $3$ dimensional shapes with $6$ rectangular faces.

The formula for the volume of a cuboid is:

Volume = length \times width \times height

Volume is measured in cubic units, e.g. $mm^3, cm^3$ or $m^3.$

This cuboid is made from $24$ unit cubes.

Its volume is

\begin{aligned} &Volume = length \times width \times height \\ &Volume = 2 \times 4 \times3 \\ &Volume = 24 \; cm^3 \end{aligned}

The units of volume are cubed units

E.g. $mm^3$ (cubic millimetres), $cm^3$ (cubic centimetres), $m^3$ (cubic metres) .

What is volume of a cuboid?

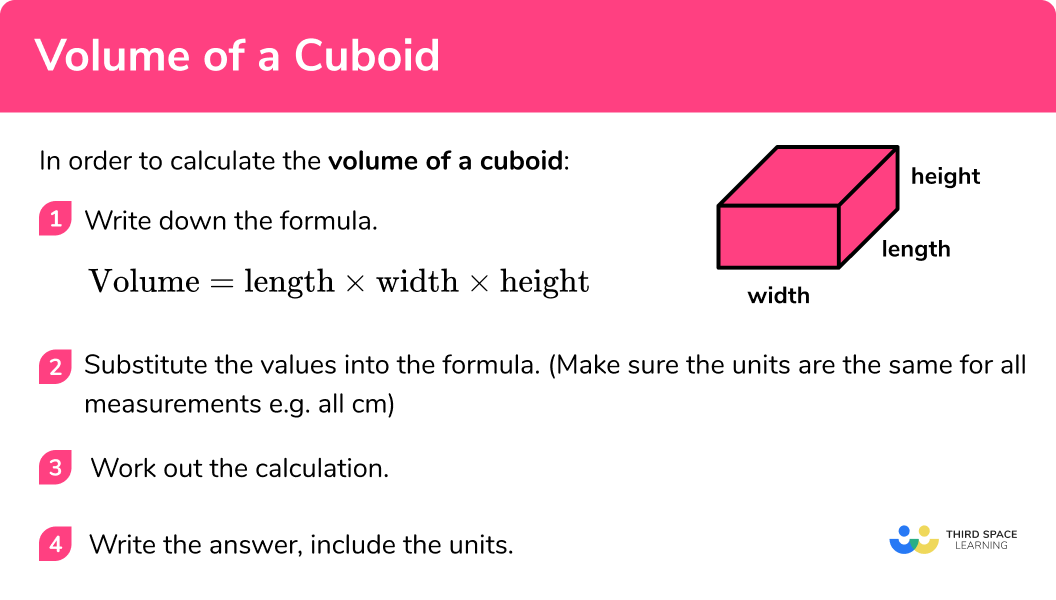
How to calculate the volume of a cuboid

In order to calculate the volume of a cuboid:

Write down the formula.

$Volume = length \times width \times height$

2Substitute the values into the formula.

Make sure the units are the same for all measurements

3Substitute the values into the formula.

4Write the answer, include the units.

How to calculate the volume of a cuboid

Volume of a cuboid worksheet

Get your free volume of a cuboid worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Volume of a cuboid worksheet

Get your free volume of a cuboid worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Volume of a cuboid examples

Example 1: volume of a cuboid

Work out the volume of the cuboid:

Write down the formula.

Volume = length \times width \times height

2Substitute the values into the formula.

Here the length is $10 \; cm$ , the width is $2 \; cm$ and the height is $5 \; cm$ .

Volume = 2 \times 10 \times 5

3Work out the calculation.

\begin{aligned} &Volume = 2 \times 10 \times 5 \\\\ &Volume = 100 \end{aligned}

4Write the answer, include the units.

The measurements are in $cm$ therefore the volume will be in $cm^3.$

Volume = 100cm^3

Example 2: volume of a cube

Work out the volume of this cube:

Write down the formula.

Volume = length \times width \times height

Substitute the values into the formula.

Since this is a cube, the length of the cuboid, width of the cuboid and height of the cuboid are all $6 \; cm.$

$Volume = 6 \times 6 \times 6$

Work out the calculation.

\begin{aligned} &Volume = 6 \times 6 \times 6 \\\\ &Volume = 216 \end{aligned}

Write the answer, include the units.

Volume=216 \; cm^3

Example 3: volume of a cuboid (different units)

Work out the volume of this cuboid:

Write down the formula.

Volume = length \times width \times height

Substitute the values into the formula.

Notice here that one of the units is in cm whilst the others are in m. We need all the units to be the same to calculate the volume.

We can change $cm$ to $m: 50cm = 0.5m.$

Now that we have all of the measurements in m, we can calculate the volume:

$Volume = 4 \times 2 \times 0.5$

Work out the calculation.

\begin{aligned} &Volume = 4 \times 2 \times 0.5 \\\\ &Volume = 4 \end{aligned}

Write the answer, include the units.

Since the measurements that we used were in metres, the volume will be in cubic metres.

$Volume=4 \; m^3$

How to work out a missing length given the volume

Sometimes we might know the volume and some of the measurements of a cuboid and we might want to work out the other measurements. We can do this by substituting the values that we know into the formula for the volume of a cuboid and solving the equation that is formed.

Write down the formula.

$Volume = length \times width \times height$

2Substitute the values that you do know into the formula.

Make sure the units are the same for all measurements

3Solve the equation.

4Write the answer, include the units.

How to work out a missing length given the volume

Missing length given the volume examples

Example 4: find the width of a cuboid given the volume

The volume of the cuboid is $56 \; cm^3$ . Work out the width of the cuboid.

Write down the formula.

Volume = length \times width \times height

Substitute the values that you do know into the formula.

In this example, we know that the volume of the cuboid is $56$ cubic centimetres, the width is $7 \; cm$ and the height is $2 \; cm.$

Substituting these into the formula:

$\begin{aligned} \text{Volume }&= \text{ length }\times \text{ width }\times \text{ height }\\\\ 56&=7 \times w \times 2\\\\ 56&=14w \end{aligned}$

Solve the equation.

\begin{aligned} 14w&= 56\\\\ w&=4 \end{aligned}

Write the answer, include the units.

Since the measurements in this question were in $cm$ and $cm^3$ , the width will be in $cm$

$w = 4 \;cm$

Example 5: find the length of a cuboid given the volume

The cuboid below has a square base. The height of the cuboid is $8 \; m$ and the volume of the cuboid is $32 \; m^3$ . Find the length of the cuboid.

Write down the formula.

Volume = length \times width \times height

Substitute the values that you do know into the formula.

In this example, we know that the volume of the cuboid is $32$ cubic metres and the height is $8 \; cm$ .

Substituting these into the formula:

$\begin{aligned} \text{Volume }&= \text{ length }\times \text{ width }\times \text{ height }\\\\ 32&=l \times w \times 8\\\\ 32&=8lw \end{aligned}$

Solve the equation.

\begin{aligned} 8lw&=32\\\\ lw&=4 \end{aligned}

Since the base is a square, we know that the length and width are the same.

Therefore we are looking for a number that, when multiplied by itself, makes $4.$ We need to find the square root of $4.$

$\sqrt{4}=2$

The length and width of this cuboid are $2.$

Write the answer, include the units.

l=2 \;m

Example 6: dimensions of a cube given the volume

Work out the dimensions of a cube which has a volume of $64 \; cm^3$

Write down the formula.

Volume = length \times width \times height

Substitute the values that you do know into the formula.

The only value we currently know is the volume is $64$ cubic $cm.$

$\begin{aligned} \text{Volume }&= \text{ length }\times \text{ width }\times \text{ height }\\\\ 64&=l \times w \times h \end{aligned}$

Solve the equation.

lwh=64

Since the shape is a cube, we know that the length, width and height are all the same. Therefore we are looking for a number that, when multiplied by itself three times, makes $64.$ We need to find the cube root of $64.$

$\sqrt[3]{64}=4$

The length, width and height of this cube are $4.$

Write the answer, include the units.

The cube is $4cm \times 4cm \times 4cm$

Common misconceptions

Missing/incorrect units

You should always include units in your answer. Volume is measured in units cubed (e.g. $mm^3, cm^3, m^3$ etc)

Calculating with different units

You need to make sure all measurements are in the same units before calculating volume.

E.g. you can’t have some in $cm$ and some in $m$

Dividing by three rather than cube rooting

If you are given the volume of a cube and you need to find the side length, remember the inverse of cubed is cube root, not divide by $3.$

E.g. if the volume of a cube is $8cm^3$ , the side length is

$\sqrt[3]{8}=2 \; \mathrm{cm}$ (not $8\div3$ )

Volume of a cuboid is part of our series of lessons to support revision on cuboid. You may find it helpful to start with the main cuboid lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Practice volume of a cuboid questions

144 \; \mathrm{cm}^{2}

12 \; \mathrm{cm}^{3}

144 \; \mathrm{cm}^{3}

36 \; \mathrm{cm}^{3}

\begin{aligned} \text{Volume }&= \text{ length }\times \text{ width }\times \text{ height }\\\\ \text{Volume }&= 12 \times 3 \times 4\\\\ \text{Volume }&=144 \; \mathrm{cm}^{3} \end{aligned}

64 \; \mathrm{m}^{3}

512 \;\mathrm{m}^{3}

8 \;\mathrm{m}^{3}

24 \; \mathrm{m}^{3}

\begin{aligned} \text{Volume }&= \text{ length }\times \text{ width }\times \text{ height }\\\\ \text{Volume }&= 8 \times 8 \times 8\\\\ \text{Volume }&=512 \; \mathrm{m}^{3} \end{aligned}

1748 \; \mathrm{cm}^{3}

174.8 \; \mathrm{m}^{3}

17.48 \; \mathrm{m}^{3}

17.48 \; \mathrm{cm}^{3}

Here there are measurements in $cm$ and $m$ so we must make the units the same before calculating the volume.

We can convert $380 \; cm$ to $3.8 \;m.$

\begin{aligned} \text{Volume }&= \text{ length }\times \text{ width }\times \text{ height }\\\\ \text{Volume }&= 2.3 \times 2 \times 3.8\\\\ \text{Volume }&=17.48 \; \mathrm{m}^{3} \end{aligned}

Since the measurements we used were in metres, the volume will be in cubic metres.

3 \; cm

24 \; cm

200 \; cm

75 \; cm

\begin{aligned} \text{Volume }&= \text{ length }\times \text{ width }\times \text{ height }\\\\ 600&= 25 \times 8 \times h\\\\ 600&=200h\\\\ h&=3\; \mathrm{cm} \end{aligned}

45 \; cm

4.5 \; cm

2.1 \; cm

6.7 \; cm

Since the base of the cuboid is a square, the length and the width are both $10 \; cm.$

\begin{aligned} \text{Volume }&= \text{ length }\times \text{ width }\times \text{ height }\\\\ 450&= 25 \times 10 \times h\\\\ 450&=100h\\\\ h&=4.5 \; \mathrm{cm} \end{aligned}

7 \; cm

114.3 \; cm

18.5 \; cm

57.2 \; cm

\begin{aligned} \text{Volume }&= \text{ length }\times \text{ width }\times \text{ height }\\\\ 343&=l \times w \times h \end{aligned}

Since this is a cube we know that the length, width and height are all equal. Therefore we are looking for a number that, when multiplied by itself $3$ times, makes $343.$ We need the cube root of $343.$

\sqrt[3]{343}=7

The length, width and height of the cube are all $7 \;cm.$

Volume of a cuboid GCSE questions

1. Work out the volume of this cuboid. Give your answer in $cm^3.$

Volume of a cuboid GCSE Question 1

(3 marks)

Show answer

0.9 \; m = 90 \;cm

(1)

\text{Volume }=90 \times 40 \times 20

(1)

\text{Volume }=72000 \; \mathrm{cm}^{3}

(1)

2. A paddling pool is in the shape of a cuboid.

Volume of a cuboid GCSE Question 2

(a) Work out the volume of the paddling pool.

(b) Sam wants to fill the pool so that it is $\frac{5}{6}$ full.

Water flows out of her hose pipe and into the pool at a rate of $20$ litres per minute.

Given that $1\;\mathrm{m}^{3}=1000 \;\mathrm{l}$ , calculate the length of time it would take Sam to fill the pool so that it is $\frac{5}{6}$ full. Give your answer in hours.

(6 marks)

Show answer

(a)
$\text{Volume }=4 \times 1.8 \times 0.6$

(1)

\text{Volume }=4.32 \; \mathrm{m}^{3}

(1)

(b)

4.32 \times 1000=4320 \; \mathrm{l}

(1)

\frac{5}{6} \text{ of } 4320 = 3600 \; \mathrm{l}

(1)

3600 \div 20=180 \text{ mins}

(1)

180 \; \text{ mins} = 3 \; \text{ hours}​

(1)

3. A carton of orange juice is shown below. The carton is completely full. The orange juice is poured into another container, as shown below.

Volume of a cuboid GCSE Question 3 Image 1

Volume of a cuboid GCSE Question 3 Image 2

What will the height of the orange juice in the container be?

(5 marks)

Show answer

\text{Volume of orange juice: }6 \times 10 \times 30

(1)

\text{Volume of orange juice: }1800 \; \mathrm{cm}^{3}

(1)

\begin{aligned} \text{Volume }&= \text{ length }\times \text{ width }\times \text{ height }\\\\ 1800&=40 \times 9 \times h \end{aligned}

(1)

1800 = 360 \;h

(1)

h = 5 \; cm

(1)

Learning checklist

You have now learned how to:

Know and apply the formula to calculate the volume of cuboids

Use the properties of faces, surfaces, edges and vertices of cubes and cuboids to solve problems in 3-D

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.