Ratio Questions And Practice Problems: Differentiated Practice Questions Included
Ratio questions appear throughout middle and high school, building on students’ knowledge year on year. Here we provide a range of ratio questions and practice problems of varying complexity to use with your own students in class or as inspiration for creating your own.
What is ratio?
Ratio is used to compare the size of different parts of a whole. For example, the total number of students in a class is 30. There are 10 girls and 20 boys. The ratio of girls:boys is 10:20 or 1:2. For every one girl there are two boys.
Ratio Worksheet
Download this quiz to check your students’ understanding of ratios. Features 10 questions with answers to identify areas of strength and support!
Download Free Now!
Uses of ratio
You might see ratios written on maps to show the scale of the map or use ratios to determine the currency exchange rate if you are going on vacation to another country.
Ratio will be seen as a topic in its own right as well as appearing within other topics. An example of this might be the area of two shapes being in a given ratio or the angles of a shape being in a given ratio.
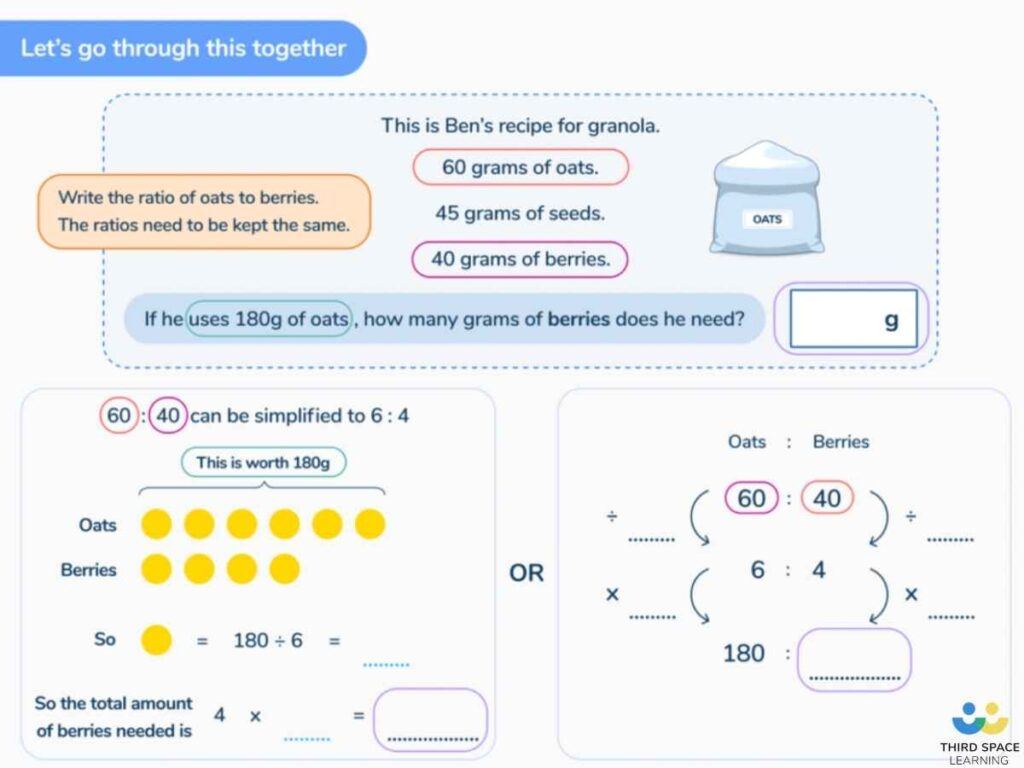
visual representations are a really useful way in.
Ratio in Middle School and High School
In middle school, ratio questions will involve writing and simplifying ratios, using equivalent ratios, dividing quantities into a given ratio and will begin to look at solving problems involving ratio. At high school, these skills are recapped and the focus will be more on ratio word problems which will require you to conduct problem solving using your knowledge of ratio.
Proportion and ratio
Ratio often appears alongside proportion and the two topics are related. Whereas ratio compares the size of different parts of a whole, proportion compares the size of one part with the whole. Given a ratio, we can find a proportion and vice versa.
Take the example of a box containing 7 counters; 3 red counters and 4 blue counters:
The ratio of red counters:blue counters is 3:4.
For every 3 red counters there are four blue counters.
The proportion of red counters is \frac{3}{7} and the proportion of blue counters is \frac{4}{7}.
3 out of every 7 counters are red and 4 out of every 7 counters are blue.
Direct proportion and inverse proportion
From 7th grade onwards, students learn about direct proportion and inverse proportion. When two things are directly proportional to each other, one can be written as a multiple of the other and therefore they increase at a fixed ratio.
How to solve a ratio problem
When looking at a ratio problem, the key pieces of information that you need are what the ratio is, whether you have been given the whole amount or a part of the whole and what you are trying to work out.
If you have been given the whole amount you can follow these steps to answer the question:
- Add together the parts of the ratio to find the total number of shares.
- Divide the total amount by the total number of shares.
- Multiply by the number of shares required.
If you have been been given a part of the whole you can follow these steps:
- Identify which part you have been given and how many shares it is worth.
- Use equivalent ratios to find the other parts.
- Use the values you have to answer your problem.
How to solve a proportion problem
As we have seen, ratio and proportion are strongly linked. If we are asked to find what proportion something is of a total, we need to identify the amount in question and the total amount. We can then write this as a fraction:
Proportion problems can often be solved using scaling. To do this you can follow these steps:
- Identify the values that you have been given which are proportional to each other.
- Use division to find an equivalent relationship.
- Use multiplication to find the required relationship.
Real life ratio problems and proportion problems
Ratio is all around us. Let’s look at some examples of where we may see ratio and proportion:
Cooking ratio question
When making yogurt, the ratio of starter yogurt to milk should be 1:9. I want to make 1,000 ml of yogurt. How much milk should I use?
Here we know the full amount – 1,000 ml.
The ratio is 1:9 and we want to find the amount of milk.
- Add together the parts of the ratio to find the total number of shares.
- Divide the total amount by the total number of shares.
- Multiply by the number of shares required.
- Total number of shares
= 1 + 9 = 10 - Value of each share:
1,000 ÷ 10 = 100 - The milk is
9 shares so9 × 100 = 900
I need to use 900ml of milk.
Maps ratio question
The scale on a map is 1:10,000. What distance would 3.5cm on the map represent in real life?
If you have been been given a part of the whole you can follow these steps:
- Identify which part you have been given and how many shares it is worth.
- Use equivalent ratios to find the other parts.
- Use the values you have to answer your problem.
Here we know one part is 3.5. We can use equivalent ratios to find the other part.
The distance in real life would be 35,000cm or 350m.
Speed proportion question
I traveled 60 miles in 2 hours. Assuming my speed doesn’t change, how far will I travel in 3 hours?
This is a proportion question.
Proportion problems can often be solved using scaling. To do this you can follow these steps:
- Identify the values that you have been given which are proportional to each other.
- Use division to find an equivalent relationship.
- Use multiplication to find the required relationship.
- I traveled 60 miles in 2 hours.
- Dividing by 2, I traveled 30 miles in one hour.
- Multiplying by 3, I would travel 90 miles in 3 hours.
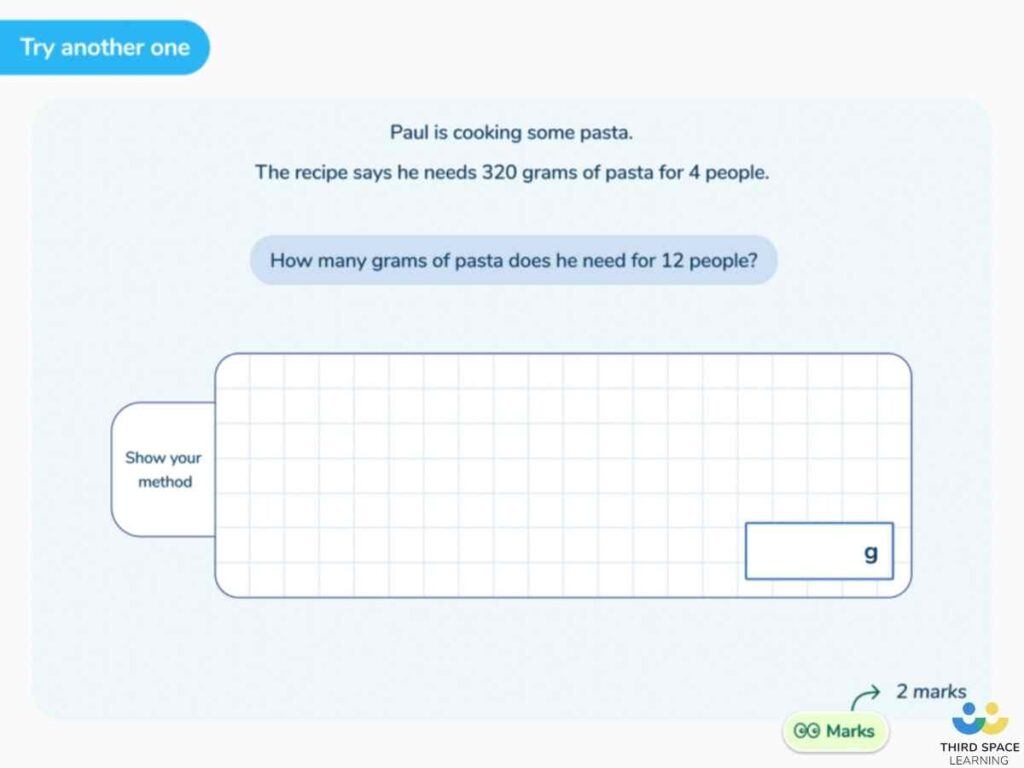
Middle School ratio questions
Ratio is introduced in middle school. Writing and simplifying ratios is explored and the idea of dividing quantities in a given ratio is introduced using proportion word problems such as the question below, before being linked with the mathematical notation of ratio.
Example Middle School worded question
Richard has a bag of 30 sweets. Richard shares the sweets with a friend. For every 3 sweets Richard eats, he gives his friend 2 sweets. How many sweets do they each eat?
Practice ratio questions for middle school
At this level, ratio questions ask you to write and simplify a ratio, to divide quantities into a given ratio and to solve problems using equivalent ratios. See below the example questions to support test prep.
Ratio questions for 6th grade
1. In Lucy’s class there are 12 boys and 18 girls. Write the ratio of girls to boys in its simplest form.




The question asks for the ratio of girls to boys, so girls must be first and boys second. It also asks for the answer in its simplest form.
2. The ratio of cups of flour to cups of water in a pizza dough recipe is 9:4. A pizza restaurant makes a large quantity of dough, using 36 cups of flour. How much water should they use?
Ratio questions 7th grade
3. The ratio of men to women working in a company is 3:5. What proportion of the employees are women?




In this company, the ratio of men to women is 3:5 so for every 3 men there are 5 women.
This means that for every 8 employees, 5 of them are women.
Therefore \frac{5}{8} of the employees are women.
4. Mac traveled 30 miles in \frac{3}{4} of an hour. Assuming his speed doesn’t change, how far will Mac travel in 1 hour?
40 miles

66 miles

22.5 miles

50 miles

We have been given a part so we can work this out using equivalent ratios.
The ratio of miles to hours is 30: \frac{3}{4} .
To create an equivalent ratio, divide each side by the same number. Since we are solving to find how far Mac will travel in 1 hour, divide both sides by \frac{3}{4} .
30: \frac{3}{4}
30 \div \frac{3}{4}: \frac{3}{4} \div \frac{3}{4}
40: 1
Mac will travel 40 miles in 1 hour.
Ratio questions 8th grade
While the Common Core State Standards does not explicitly include ratio and proportional relationships in the 8th grade, it may pop up on your own curriculums and offers a good opportunity to revisit and extend their knowledge of ratio and proportion before they enter high school.
5. The angles in a triangle are in the ratio 3:4:5. Work out the size of each angle.
30^{\circ} , 40^{\circ} and 50^{\circ}

22.5^{\circ}, 30^{\circ} and 37.5^{\circ}

60^{\circ} , 60^{\circ} and 60^{\circ}

45^{\circ} , 60^{\circ} and 75^{\circ}

The angles in a triangle add up to 180 ^{\circ} . Therefore 180 ^{\circ} is the whole and we need to divide 180 ^{\circ} in the ratio 3:4:5.
The total number of shares is 3 + 4 + 5 = 12.
Each share is worth 180 ÷ 12 = 15 ^{\circ} .
3 shares is 3 x 15 = 45 ^{\circ} .
4 shares is 4 x 15 = 60 ^{\circ} .
5 shares is 5 x 15 = 75 ^{\circ} .
6. Paint Pro makes pink paint by mixing red paint and white paint in the ratio 3:4.
Colour Co makes pink paint by mixing red paint and white paint in the ratio 5:7.
Which company uses a higher proportion of red paint in their mixture?
They are the same

Paint Pro

Colour Co

It is impossible to tell

The proportion of red paint for Paint Pro is \frac{3}{7}
The proportion of red paint for Colour Co is \frac{5}{12}
We can compare fractions by putting them over a common denominator using equivalent fractions
\frac{3}{7} = \frac{36}{84} \hspace{3cm} \frac{5}{12}=\frac{35}{84}
\frac{3}{7} is a bigger fraction so Paint Pro uses a higher proportion of red paint.
High school ratio questions
At high school, we apply the knowledge that we have of ratios to solve different problems. Ratio can be linked with many different topics, for example similar shapes and probability, as well as appearing as problems in their own right.
Ratio high school questions (low difficulty)
7. The students in Ellie’s class walk, cycle or drive to school in the ratio 2:1:4. If 8 students walk, how many students are there in Ellie’s class altogether?




We have been given one part so we can work this out using equivalent ratios.
The total number of students is 8 + 4 + 16 = 28
8. A bag contains counters. 40% of the counters are red and the rest are yellow.
Write down the ratio of red counters to yellow counters. Give your answer in the form 1:n.




If 40% of the counters are red, 60% must be yellow and therefore the ratio of red counters to yellow counters is 40:60. Dividing both sides by 40 to get one on the left gives us
Since the question has asked for the ratio in the form 1:n, it is fine to have decimals in the ratio.
9. Rosie and Jim share some sweets in the ratio 5:7. If Jim gets 12 sweets more than Rosie, work out the number of sweets that Rosie gets.




Jim receives 2 shares more than Rosie, so 2 shares is equal to 12.
Therefore 1 share is equal to 6. Rosie receives 5 shares: 5 × 6 = 30.
10. Rahim is saving for a new bike which will cost $480. Rahim earns $1,500 per month. Rahim spends his money on bills, food and extras in the ratio 8:3:4. Of the money he spends on extras, he spends 80% and puts 20% into his savings account.
How long will it take Rahim to save for his new bike?
1 month

6 months

3 months

5 months

Rahim’s earnings of $1,500 are divided in the ratio of 8:3:4.
The total number of shares is 8 + 3 + 4 = 15.
Each share is worth $1,500 ÷ 15 = £100.
Rahim spends 4 shares on extras so 4 × $100 = $400.
20% of $400 is $80.
The number of months it will take Rahim is $480 ÷ $80 = 6
Ratio GCSE exam questions higher
11. The ratio of milk chocolates to white chocolates in a box is 5:2. The ratio of milk chocolates to dark chocolates in the same box is 4:1.
If I choose one chocolate at random, what is the probability that that chocolate will be a milk chocolate?




To find the probability, we need to find the fraction of chocolates that are milk chocolates. We can look at this using equivalent ratios.
To make the ratios comparable, we need to make the number of shares of milk chocolate the same in both ratios. Since 20 is the LCM of 4 and 5 we will make them both into 20 parts.
We can now say that milk to white to dark is 20:8:5. The proportion of milk chocolates is \frac{20}{33} so the probability of choosing a milk chocolate is \frac{20}{33} .
12. In a school the ratio of girls to boys is 2:3.
25% of the girls have school dinners.
30% of the boys have school dinners.
What is the total percentage of students at the school who have school dinners?




In this question you are not given the number of students so it is best to think about it using percentages, starting with 100%.
100% in the ratio 2:3 is 40%:60% so 40% of the students are girls and 60% are boys.
25% of 40% is 10%.
30% of 60% is 18%.
The total percentage of students who have school dinners is 10 + 18 = 28%.
13. For the cuboid below, a:b = 3:1 and a:c = 1:2.
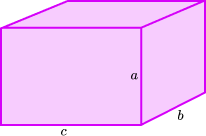
Find an expression for the volume of the cuboid in terms of a.




If a:b = 3:1 then b=\frac{1}{3}a
If a:c = 1:2 then c=2a.

Ratio high school questions (average difficulty)
14. Bill and Ben win some money in their local lottery. They share the money in the ratio 3:4. Ben decides to give $40 to his sister. The amount that Bill and Ben have is now in the ratio 6:7.
Calculate the total amount of money won by Bill and Ben.
$560

$70

$140

$600

Initially the ratio was 3:4 so Bill got $3a and Ben got $4a. Ben then gave away $40 so he had $(4a-40).
The new ratio is 3a:4a-40 and this is equal to the ratio 6:7.
Since 3a:4a-40 is equivalent to 6:7, 7 lots of 3a must be equal to 6 lots of 4a-40.
\begin{aligned} \\ 7 \times 3a &= 6 \times (4a-40)\\\\ 21a&=24a-240\\\\ 3a&=240\\\\ a&=80 \end{aligned}
The initial amounts were 3a:4a. a is 80 so Bill received $240 and Ben received $320.
The total amount won was $560.
15. On a farm the ratio of pigs to goats is 4:1. The ratio of pigs to piglets is 1:6 and the ratio of goats to kids is 1:2.
What fraction of the animals on the farm are babies?




The easiest way to solve this is to think about fractions.
\\ \frac{4}{5} of the animals are pigs, \frac{1}{5} of the animals are goats.
\frac{1}{7} of the pigs are adult pigs, so \frac{1}{7} of \frac{4}{5} is \frac{1}{7} \times \frac{4}{5} = \frac{4}{35}
\frac{6}{7} of the pigs are piglets, so \frac{6}{7} of \frac{4}{5} is \frac{6}{7} \times \frac{4}{5} = \frac{24}{35}
\frac{1}{3} of the goats are adult goats, so \frac{1}{3} of \frac{1}{5} is \frac{1}{3} \times \frac{1}{5} = \frac{1}{15}
\frac{2}{3} of the goats are kids, so \frac{2}{3} of \frac{1}{5} is \frac{2}{3} \times \frac{1}{5} = \frac{2}{15}
The total fraction of baby animals is \frac{24}{35} + \frac{2}{15} = \frac{72}{105} +\frac{14}{105} = \frac{86}{105}
Looking for more middle school and high school ratio math questions?
Try these:
- Algebra questions
- Probability questions
- Trigonometry questions
- Venn diagram questions
- Long division questions
- Pythagorean theorem questions
Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.
Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.
Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring
Why not learn more about how it works?





