Long Division Problems That Will Test All Students From Sixth Grade to Seniors
Some division questions are designed for students to practice dividing large numbers such as a four digit number by a two digit number or a three digit number commonly. When larger numbers are involved, students will often use the standard algorithm, or long division.
Here is a selection of long division questions you can share with your students to help them work through the steps involved in using long division.
Teaching Long Division Worksheets
Long division can be tough, download this free worksheet for Grades 3-5 to help your students better understand long division.
Download Free Now!Long division key terminology
Let’s recap some key points:
- The division symbol looks like this: ÷
- The dividend is the number we are dividing.
- The divisor is the number we are dividing by.
- The quotient is the quantity produced by the division.
What is the long division algorithm
We can think of long division as a step by step process in which the steps are repeated until the calculation is complete.
When completing a long division calculation, the first thing we do is write out the first 9 multiples of the divisor. This makes the next steps a lot easier. Once we have done this, we can follow these long division steps:
- Divide
- Multiply
- Subtract
- Bring the next digit down
If you have been struggling to teach long division to your 6th grade class then this post on the long division method step by step will prove invaluable!
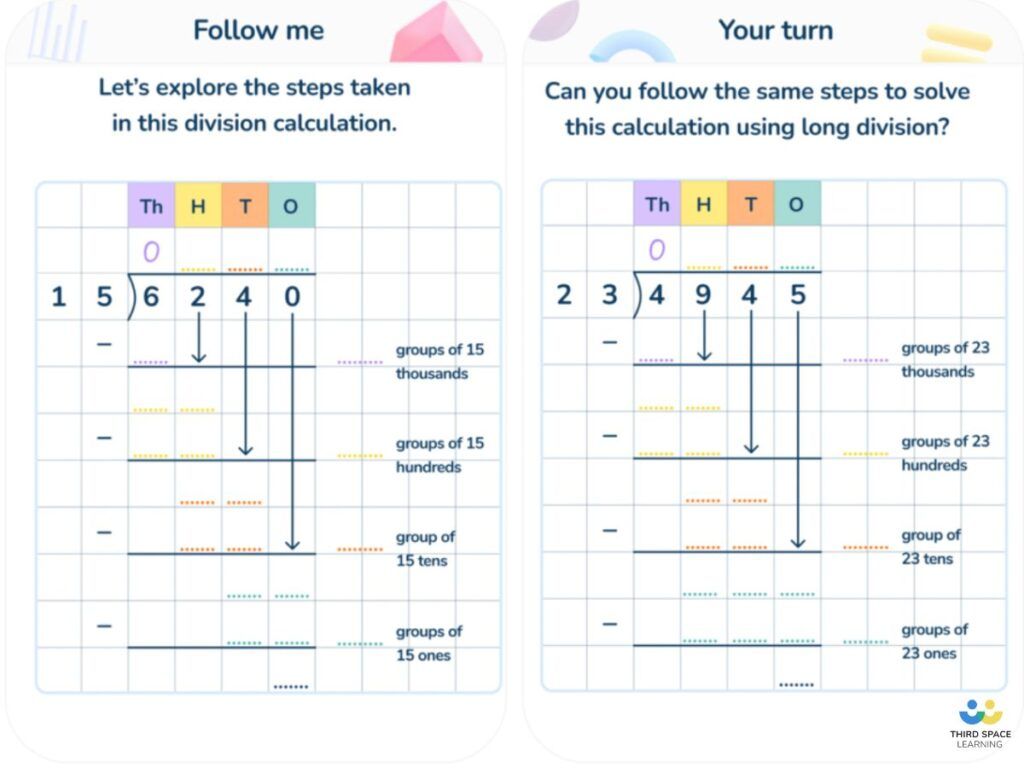
Long division question example
Let’s look at an example:
1752 ÷ 24
First, write out the first 9 multiples of 24. This can be worked out either using partitioning or by repeated addition.
By writing out the multiples of 24, you are saving yourself the time of working through the 24 times table mentally several times, as well as ensuring you make less mistakes.
Multiples of 24:
24, 48, 72, 96, 120, 144, 168, 192, 216, …
Now follow the steps:
- Divide: how many times does 24 go into 175?
It goes in 7 times (I can see this from my multiples)
- Multiply: 24 x 7 = 168 (Again I can see this from multiples). Ensure you align the place values correctly when placing this on the grid.
- Subtract: 175 – 168 = 7
- Bring down: bring down the 2
Repeat:
- Divide: how many times does 24 go into 72?
It goes in 3 times
- Multiply: 24 x 3 = 72
- Subtract: 72 – 72 = 0
- The answer to the subtraction here is 0, therefore the remainder is zero and we are finished
In some long division problems the divisor does not divide the dividend a whole number of times and in these cases the answer may be written with a remainder or a decimal.
The Common Core State Standards states that we need to be able to interpret remainders as whole number remainders, decimals, or by rounding, as appropriate for the context.
Long division questions for 5th grade
Students sometimes first encounter long division around 4th grade, typically finding whole number quotients using one-digit divisors and multi-digit dividends.
As students’ skills develop across 5th grade, questions typically involve two-digit divisors. Beginning in 6th grade, students apply the same understanding to dividing multi-digit decimals.
As students progress through the process of long division, they then apply the same method to divide numbers to reasoning and word problems. It is important that students have a good understanding of the basic multi-digit multiplication and division process.
Long division questions for 5th grade
1. Calculate 4488 ÷ 34




The multiples of 34 are: 34, 68, 102, 136, 170, 204, 238, 272, 306,…
2. Work out 6720 ÷ 25




The multiples of 25 are: 25, 50, 75, 100, 125, 150, 175, 200, 225, …
3. Calculate 9129 ÷ 68.



The multiples of 68 are: 68, 136, 204, 272, 340, 408, 476, 544, 612, …
4. What is the remainder when 3810 is divided by 47?




The multiples of 47 are: 47, 94, 141, 188, 235, 282, 329, 376, 423, …
Long division questions for 6th grade
5. Nadim is calculating 4482 ÷ 54. His calculation is shown below.
Nadim has made a mistake. Which of the circled numbers is incorrect?




0 is incorrect. He should have brought the 2 down.
6. A zoo charges £13 per ticket. In one day the zoo took £6,136 in ticket sales. How many people visited the zoo that day?




The calculation we need to do is £6,136 ÷ 13
The multiples of 13 are: 13, 26, 39, 52, 65, 78, 91, 104, 117, …
472 people visited the zoo that day.
7. Sophia is going to make some bracelets. Each bracelet uses 77 beads. Sophia has 3500 beads. How many bracelets can Sophia make?




We need to work out 3500 ÷ 77
The multiples of 77 are: 77, 154, 231, 308, 385, 462, 539, 616, 693, …
Sophia can make 45 bracelets. She will have 35 beads left over.
8. A shopkeeper sells pineapples for $0.93 each. One week he sells $91.14 worth of pineapples. How many pineapples did he sell that week?




£91.14 is the same as 9114p. In this case it makes more sense to multiply by 100 and work in pence than to work with decimals.
9114 ÷ 93:
Multiples of 93: 93, 186, 279, 372, 465, 558, 651, 744, 837, …
He sold 98 pineapples.
9. Below is a calculation. Some numbers have been covered up.
What number should appear in place of the triangle?




Subtracting 136 from 1__0 gives us 54.
136 + 54 = 190, so the number under the square should be 9.
68 + 19 = 87, so the number under the triangle should be 7.
(The number under the circle should be 6 since 1 multiplied by the number gives us 68.)
10. Lucy buys a car for $7500. She pays $4080 up front and splits the rest of the cost over 36 months. Work out how much she pays each month.




£7500 – £4080 = £3420.
She has £3420 to pay so we need to calculate £3420 ÷ 36
The multiples of 36 are: 36, 72, 108, 144, 180, 216, 252, 288, 324, …
She will pay £95 each month.
11. The area of this rectangle is 1224cm ^2 .
Find the length of the base of the rectangle.




Since area = base × height, 1224 = base × 17
We need to calculate 1224 ÷ 17
The multiples of 17 are: 17, 34, 51, 68, 85, 102, 119, 136, 153,….
The length of the base is 72cm.
Long division in middle school and high school
Long division is not taught explicitly past the 6th grade but it can come in useful when solving division problems. It is expected that students can apply multiplication and division skills such as long multiplication and long division across all areas of the middle school and high school math curriculum, including dividing decimals and fractions.
Below are some examples of questions for high school level students where math skills in long division could be applied.
Long division questions for middle and high school
12. The probability of winning a game is \frac{3}{13} . If 845 people play the game, how many would you expect to win?




We need to calculate \frac{3}{13} of 845.
845 ÷ 13:
The multiples of 13 are:
13, 26, 39, 52, 65, 78, 91, 104, 117, …
65 × 3 = 195
You would expect 195 people to win.
13. Solve the equation 23(2x + 1) = 1219




The multiples of 46 are: 46, 92, 138, 184, 230, 276, 322, 368, 414, …..
x = 26
Looking for more middle school and high school long division math questions?
Try these:
- Ratio questions
- Algebra questions
- Probability questions
- Trigonometry questions
- Venn diagram questions
- Pythagorean theorem questions
Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.
Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.
Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring
Why not learn more about how it works?
The content in this article was originally written by secondary teacher Beki Christian and has since been revised and adapted for US schools by elementary math teacher Christi Kulesza.

