What Is The Quotient? A Step-by-Step Guide For Students And Teachers

Finding the quotient is a key skill in math from grade 3 onwards. In this article, we break down step by step how to support students to find the quotient.

Understanding operations is all about recognizing the situations or actions that are associated with each operation. They are active. Primary learners first recognize that addition represents the action of putting together or adding to, and that subtraction represents the action of taking from.

In third grade, students begin to explore the operations of multiplication and division and their inverse relationship. Finding the quotient through division helps students to visualize how many groups (quotative division) or how many objects are in each group (partitive division). These initial experiences with finding the quotient support learners in solving real-world mathematical problems. It is an important foundational skill and will be relied on to generalize patterns in numbers as students progress through higher mathematics.

What is the quotient?

The definition of quotient is the result of dividing one quantity by another. Here is an example of quotient in a division problem:

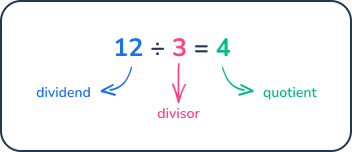
The result of the division example sentence above is 4, so 4 is the quotient. The number that is being divided, 12, is the dividend and the number that divides the given number into equal groups, 3, is the divisor.

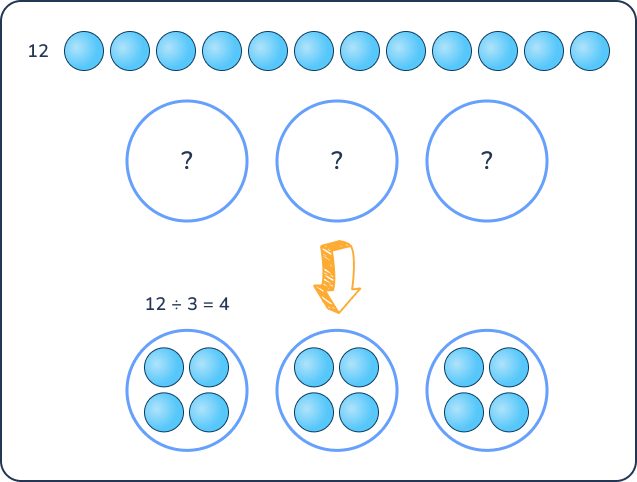
The quotient in the above example is a whole number because the dividend, 12, is a perfect division, i.e. able to be divided into equal groups of three (see below).

The quotient can also be a decimal. This happens when the dividend cannot be divided into equal groups (see below).

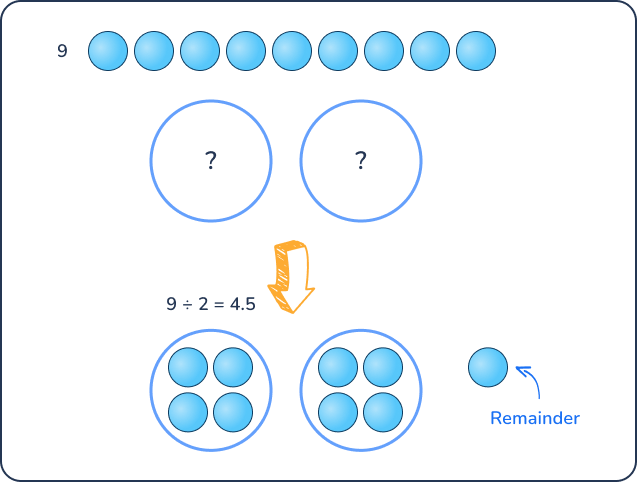
Decimal quotients leave a remainder. We discuss decimal quotients and remainders in further detail later in the article.

How to find the quotient

Finding the quotient first starts in third grade and students will learn different ways to find the quotient as they advance on their mathematics journey. Let’s take a look at a progression of strategies for finding the quotient.

Finding the quotient by repeated subtraction

When students first experience concrete representations of division situations, it is through the idea that there is a total number of objects that need to be physically split or divided into equal groups. This can be accomplished through repeated subtraction: subtracting the divisor from the dividend until subtraction is no longer possible.

Here’s an example:

Mr. Kent got a new bookshelf. The book has 5 shelves and can hold a total of 25 books. How many shelves can fit on each shelf?

In this example, the dividend is 25 and the divisor is 5. We will use repeated subtraction to find the quotient of 25 ÷ 5. 

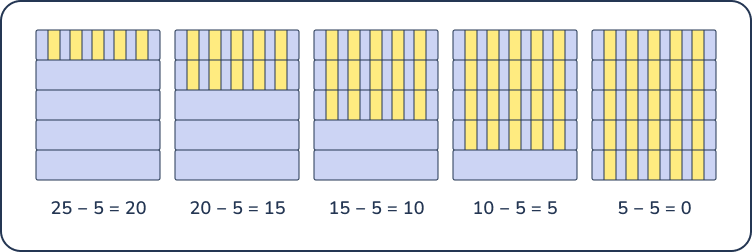
In the diagram above, we subtract 5 five times until subtraction is no longer possible. Thus, the quotient of 25 ÷ 5 is 5.

In fourth grade, students begin to experience finding the quotient with multi-digit numbers and transition from using repeated subtraction to partial quotients. Below is an example of partial quotients.

1,176 ÷ 8 = ?

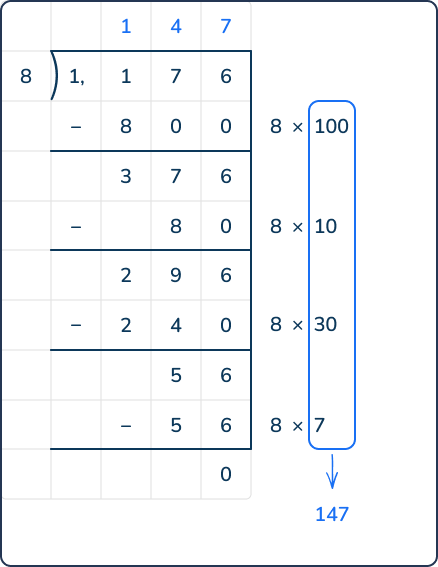
The partial quotients strategy allows students to think of division as the inverse of multiplication. It requires them to find different ways to group that can be subtracted from the total or dividend. This allows for flexible thinking and for students to use their strengths of multiplication to support their thinking around finding the quotient.

Finding the quotient by long division method

As students transition from concrete representations to partial products, students begin to be introduced to the standard algorithm of long division, also known as the long division method. This method requires an abstract understanding of our place value system. Here’s a long division example with a step by step process:

94 ÷ 4 = ?

First, set up the equation. Below is the traditional bracket notation that identifies the dividend, 96, and the divisor, 4.

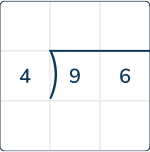
We know that we have a total of 96 and need to know how many groups of 4 there are. The process for long division is described below:

1. Divide
2. Multiply
3. Subtract
4. Bring the next digit down
5. Repeat until you have reached the solution (if possible)

This process is linked to the partial quotients method of finding the quotient but allows for more abstract thinking.

Quotient and remainders

The remainder in division is the remaining part of the total value after performing division. This part is remaining because the dividend was not completely divisible by the divisor so we are left with the remainder once the division is done. Students first experience division with remainders in fourth grade mathematics.

Concrete materials and math manipulatives such as counters help students to model situations with a remainder and visually see that there are counters left over. When learners encounter division word problems with a remainder, they need to be able to interpret the remainder with respect to the context. Here are some ways to interpret the remainder:

Ignore the remainder

Example: Sasha is buying new clothes for the school year. She is buying shirts that are $8.00 each. Sasha has $50.00. How many shirts can Sasha buy?

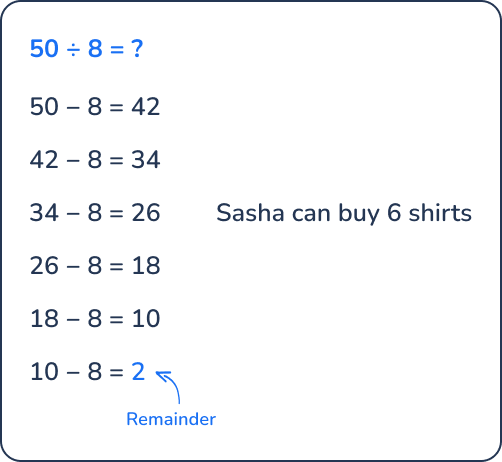
This word problem requires us to think about how many shirts Sasha can afford with the money she has. Since Sasha starts out with $50, we can repeatedly subtract $8 (the cost of one shirt) until Sasha does not have enough money left. When we subtract $8 six times, Sasha is left with only $2, which is the remainder.

This means that Sasha has enough money to buy 6 shirts since that is the number of times we subtracted a group of 8, and she still has $2 left over. Sasha does not have enough money left to buy another shirt, so we can ignore the remainder and say that Sasha can buy 6 shirts with her $50.

Increase the quotient

Example: Small Elementary’s fifth grade class is going on a field trip to the museum. There are 50 students in the fifth grade classes altogether and the vans can hold 8 students each. How many vans do they need?

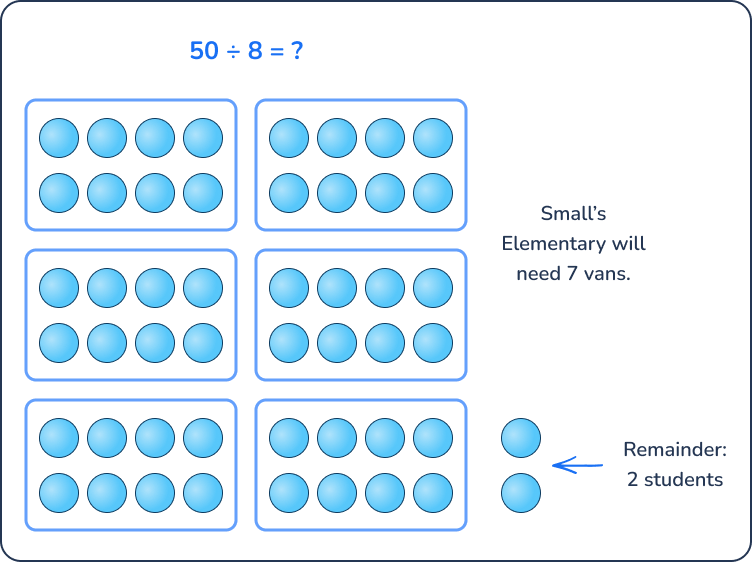
In this story, it’s important to remember that we are thinking about 50 students getting on a van to go on the field trip and that all 50 students are going.

When 50 is divided by 8, you can make 6 groups of 8 with a remainder of 2. The remainder represents 2 students who do not fit on the 6 vans, so we need to increase the quotient to 7 so all students can go on the field trip. Thus, Small’s Elementary will need 7 vans.

Remainder as a fraction or decimal

Example: There are 50 yards of fabric to make 8 scarves. How many yards of fabric will each scarf be?

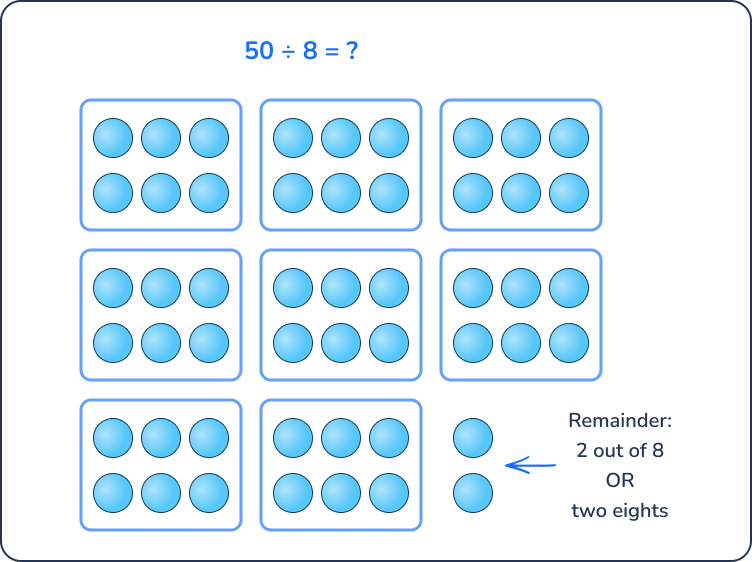
Each scarf will need 6\frac{2}{8} yards of fabric.

When 50 is divided by 8, you can make 8 groups of 6 with a remainder of 2. In this math story, fabric can be split into fractional parts that are meaningful to the story. It makes sense that fabric can be a fraction of a yard.

Thus, we can interpret the remainder as a fraction so that each scarf will need 6\frac{2}{8} yards of fabric. The numerator, 2, represents the remainder of yarn, and the denominator, 8, represents the total amount of yards that would make an equal group.

Notice that our correct answer is written as a mixed number. This quotient could also be written in different forms, such as 6\frac{1}{4} yards or as a decimal number, 6.25 yards.

When do students learn about quotients?

Finding a quotient is most suited to students in Grades 3-12. Students first learn about quotients in third grade, with a focus on the meaning of multiplication and division and their relationship with factors 0-12. This experience is very hands-on, with the use of concrete manipulatives. Repeated subtraction is a pattern students begin to connect to division. This is extremely crucial because it’s something students will rely on throughout their educational path.

In fourth grade, students begin to experience dividing multi-digit whole numbers and interpreting the remainder. Since repeated subtraction would become very cumbersome with large dividends, students begin to experience different strategies for finding the quotient, such as partial quotients and the area model. These algorithms rely heavily on place value understanding and a strong foundation of their basic math facts is required.

By fifth grade, students apply their knowledge of whole number quotients and extend it to fractions and decimals. Again, students begin with visual representations and then transition to the use of an algorithm. All this work helps to prepare students for representing and interpreting expressions through algebraic methods in middle and high school.

Quotient worked examples

Quotient worked example 1: 4th grade

372 ÷ 12 = ?

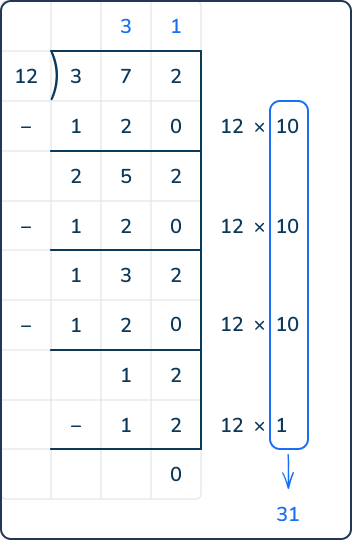
In this example, we used partial quotients to help us find the quotient. To do this, we first need to identify that the dividend or total is 372 and the divisor is 12. Then, we remove equal groups from the dividend in order to find the quotient. Thus, 372 ÷ 12 = 31.

Quotient worked example 2: 4th grade

Mrs. Nantucket has 130 apples. 4 apples fit in a basket. How many baskets does she need for all the apples?

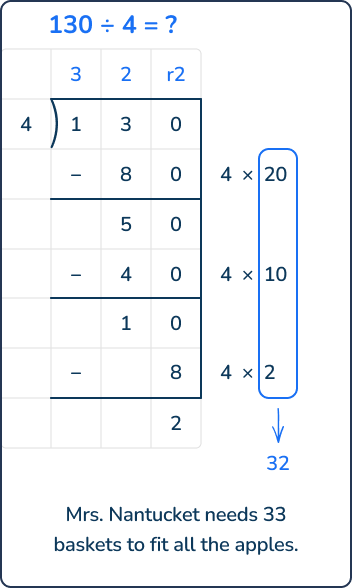
In this story, it’s important to remember that we are thinking about 130 apples being put into baskets. All 130 apples need to fit in a basket. When 130 is divided by 4, you can make 32 groups of 4 with a remainder of 2. The remainder represents 2 apples do not fit in the 32 baskets, so we need to increase the quotient to 33 so that all the apples fit in the basket. Thus, the final answer is Mr. Nantucket needs 33 baskets for all the apples.

Quotient worked example 3: 4th grade

At the fair, Jenna has 40 ride tickets. Each ride on the ferris wheel costs 7 tickets. How many times can Jenna go on the ferris wheel?

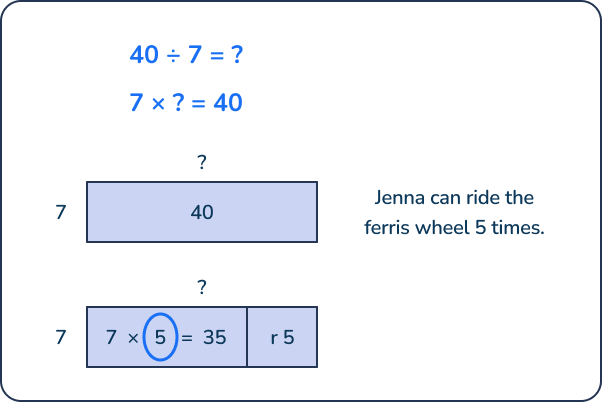
Since Jenna starts out with 40 ride tickets, we can use an area model to help us. We know that 7 x 5 = 35. This leaves us with a remainder of 5 in order to make 40. This means that Jenna has ride tickets to ride the ferris wheel 5 times, with 5 tickets left over. Even though she has 5 tickets left over, it is not enough tickets to ride the ferris wheel again, so we can ignore the remainder.

Quotient worked example 4: 5th grade

A roll of toilet paper is 10 feet long. Each sheet is \frac{1}{2} of a foot long. How many sheets are on the roll?

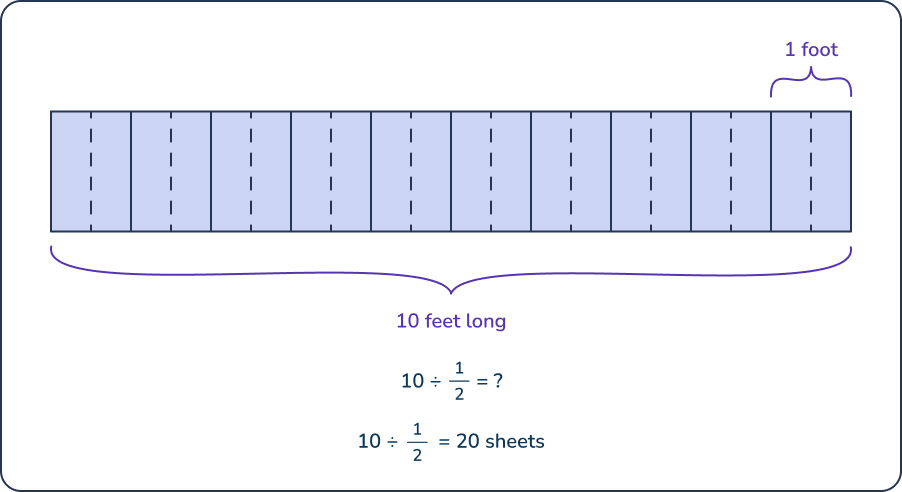
10 ÷ \frac{1}{2} = ?

10 ÷ \frac{1}{2}= 20 sheets

In this math story, we started by creating 10 feet of toilet paper. Then, we partitioned each sheet in half. This action is represented by the dotted lines. 10 divided by half has the same meaning as the question: How many halves are in 10? Thus, there are 20 halves in 10, so 10 ÷ \frac{1}{2}= 20 sheets.

Quotient practice problems

Here are a few practice problems which require students to find the quotient. The word problems below relate to real-life situations where finding the quotient is needed. Remember that it’s important to understand the meaning of the quotient, and how to interpret the remainder.

Quotient practice problem 1: 4th grade

54,180 ÷ 5 = ?

Answer: 10,836

Quotient practice problem 2: 4th grade

A baseball team needs to order 200 tennis balls for a tournament. If there are 3 balls in each can, how many cans should the team order?

Answer: 67 cans

Quotient practice problem 3: 4th and 5th grade

Paint kits are on sale for $12.00 each, including tax. How many paint kits can Janice buy with $65.00?

Answer: 5 paint kits

Quotient practice problem 4: 5th grade

Ben is bringing in a snack for his classroom tomorrow and wants to bring in oranges. He has 12 oranges. If each person gets \frac{1}{2} of an orange, how many people can have an orange?

Answer: 24 people

In addition to teaching and learning resources for finding the quotient, including long division worksheets, Third Space Learning also offers one-to-one online tutoring to support students. Personalized to the needs of each individual child, our online tutoring courses aim to fill gaps in learning and boost confidence in math. 

Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.

Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.

Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring

Why not learn more about how it works?