What Is The Concrete Representational Abstract (CRA) Approach And How To Use It In Your Elementary Math Classroom

December 17, 2024 | 7 min read

Emma Johnson

The Concrete Representational Abstract approach is now an essential tool in teaching math at elementary school, so here we explain what it is, why its use is so widespread, what misconceptions there may be around using concrete resources throughout a child’s primary math education, and how best to use the CRA approach yourself in math lessons.

In this blog, we will be focusing specifically on how the CRA approach can be used to support the teaching and learning of the four written calculation methods.

CRA diagramme — The CRA approach illustrated by one of our Third Space Learning resources

What is the Concrete Representational Abstract approach in Math?

The Concrete Representational Abstract (CRA) approach is a system of learning that uses physical and visual aids to build a child’s understanding of abstract topics.

Decimal Place Value Chart

Download this printable decimal place value chart from millionths up to millions. Contains blank place value templates for your pupils to write on.

Download Free Now!

Students are introduced to a new mathematical concept through the use of concrete resources (e.g. fruit, base ten blocks, fraction bars, etc). When they are comfortable solving problems with physical aids, they are given problems with pictures – usually visual representations of the concrete objects they were using.

Then they are asked to solve problems where they only have the abstract, i.e. numbers or other symbols. Building these steps across a lesson can help students better understand the relationship between numbers and the real world, and therefore helps secure their understanding of the mathematical concept they are learning.

Origins of Concrete Representational Abstract Approach

Looking at the origins of the CRA approach, we need to go back to the teaching methods of the 1960s, when American psychologist Jerome Bruner proposed this approach as a means of scaffolding learning.

He believed the abstract nature of learning (which is especially true in math) to be a ‘mystery’ to many children. It, therefore, needs to be scaffolded by the use of effective representations and math manipulatives.

He found that when students used the CRA approach in math, they were able to build on each stage towards a greater mathematical understanding of the concepts being learned, which in turn led to information and knowledge being internalized to a greater degree.

Many teachers mistakenly believe the CRA approach to have been a method imported from Singapore.

In actual fact, the Singapore Math curriculum has been heavily influenced by a combination of Bruner’s ideas about learning and recommendations from the 1982 Cockcroft Report (a report by the HMI in England, which suggested that computational skills should be related to practical situations and applied to problems).

Why use the Concrete Representational Abstract approach in Math?

Students achieve a much deeper understanding if they don’t have to resort to rote learning and are able to solve problems without having to memorize.

When teaching reading to young children, we accept that children need to have seen what the word is to understand it. Putting together the letters c- a- t would be meaningless and abstract if children had no idea what a cat was or had never seen a picture.

People often don’t think of this when it comes to math but to children, many mathematical concepts can be equally meaningless without a concrete resource or picture to go with it. This applies equally to mathematics teaching at elementary school.

What is a ‘Concrete’ representation in the CRA approach?

As part of the CRA approach, new concepts are introduced through the use of physical objects or practical equipment. These can be physically handled, enabling children to explore different mathematical concepts. These are sometimes referred to as math manipulatives and can include ordinary household items such as straws or dice, or specific mathematical resources such as base ten blocks or ten frames.

The abstract nature of math can be confusing for children, but through the use of concrete materials, they are able to ‘see’ and make sense of what is actually happening.

Previously, there has been the misconception that concrete resources are only for learners who find math difficult. In fact, concrete resources can be used in a great variety of ways at every level. All children, regardless of ability, benefit from the use of practical resources in ensuring understanding goes beyond the learning of a procedure.

Practical resources promote reasoning and discussion, enabling children to articulate and explain a concept. Teachers are also able to observe the children in order to gain a greater understanding of where misconceptions lie and to establish the depth of their understanding.

An explanation of the concrete part of the CPA approach — Tangible objects help children to represent numbers by observing the concrete method.

How can we portray the “representational” part of the CRA approach?

Once children are confident with a concept using concrete resources, they progress to drawing visual representations or quick sketches of the objects. By doing this, they are no longer manipulating the physical resources but still benefit from the visual support the resources provide.

Some teachers choose to leave the representational stage (also known as semi-concrete) out, but it is key to ensuring that children can make the link between a concrete resource and abstract notation. Without it, children can find actually visualizing a problem difficult.

One of the most common methods used in the representational stage is the bar model, often used in more complex multi-step problem solving.

Read more: What is a bar model

visualisation diagramme — Visualization through pictures is the next step as we see here

What is an ‘Abstract’ representation in the CRA approach?

Once children have a secure understanding of the concept through the use of concrete resources and visual images, they are then able to move on to the abstract stage. Here, children are using abstract symbols to model problems – usually numerals. To be able to access this stage effectively, children need access to the previous two stages alongside it.

For the most effective learning to take place, children need to constantly go back and forth between each of the stages. This ensures concepts are reinforced and understood.

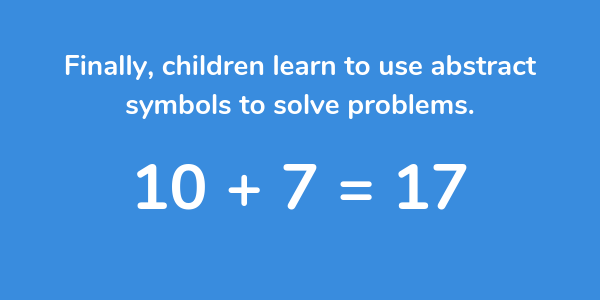
An image of the abstract part of the CPA approach — Typically written math problems like this will now be more approachable.

How to teach using the Concrete Representational Abstract method in elementary school

A common misconception with the CRA model is that you teach the concrete, then the representational, and finally the abstract. But all stages should be taught simultaneously whenever a new concept is introduced and when the teacher wants to build further on the concept.

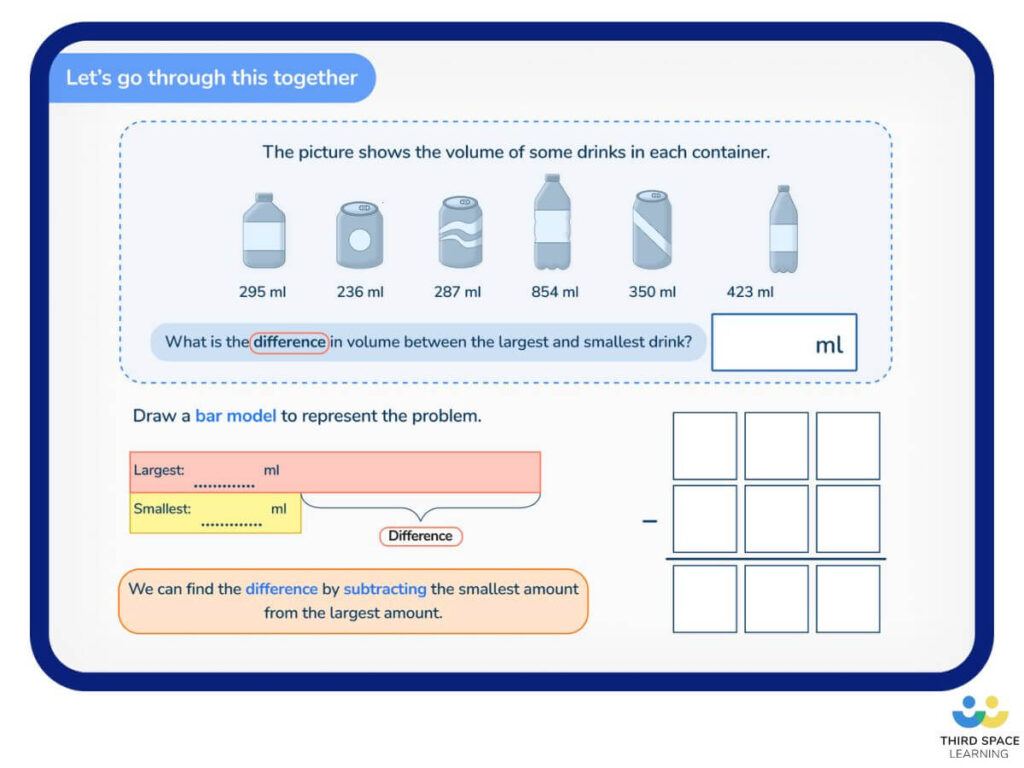
diagram lesson slide — The bar model in action in a Third Space Learning 1-to-1 lesson.

When concrete resources, visual representations and abstract recordings are all used within the same activity, it ensures students are able to make strong links between each stage.

If you’re concerned about differentiating effectively using the CRA approach, have a look at our differentiation strategies guide for ideas to get you started.

Using ‘The Four Operations’ to model how CRA works

Diagram of the 'four operations' in mathematics — ‘The four operations’ we approach in elementary level math.

In the following section, we will be looking at the ‘four operations’ and how the CRA approach can be used at different stages of teaching them. In particular, we will examine how the 3 parts of the CRA approach should be intertwined rather than taught as 3 separate things.

As this blog is to share ideas rather than say how the calculation methods should be taught, we will only cover the four operations briefly.

Teaching addition using the Concrete Representational Abstract approach

In the early stages of learning column addition, it is helpful for children to use familiar objects. For example, straws or lollipop sticks can be bundled into groups of ten and used individually to represent the tens and ones.

Once children are familiar with making 2-digit numbers using these resources, they can set the resources out on a baseboard to represent the two numbers in a column addition calculation.

Column addition straws — The concrete method sees lollipop sticks used by a teacher to differentiate between digits.

Initially, children complete calculations where the units do not add to more than 9, before progressing to calculations involving exchanging/regrouping. Alongside the concrete resources, children can annotate the baseboard to show the digits being used, which helps to build a link towards the abstract formal method.

Once children are confident using the concrete resources they can then record them representationally, again recording the digits alongside to ensure links are constantly being made between the concrete, representational and abstract levels.

The next step is for children to progress to using more formal mathematical equipment. Base ten blocks should be introduced alongside the straws, to enable children to see what is the same and what is different. As confidence grows using the base ten blocks, children can be introduced to the hundreds column for column addition, adding together 3-digit and 2-digit numbers

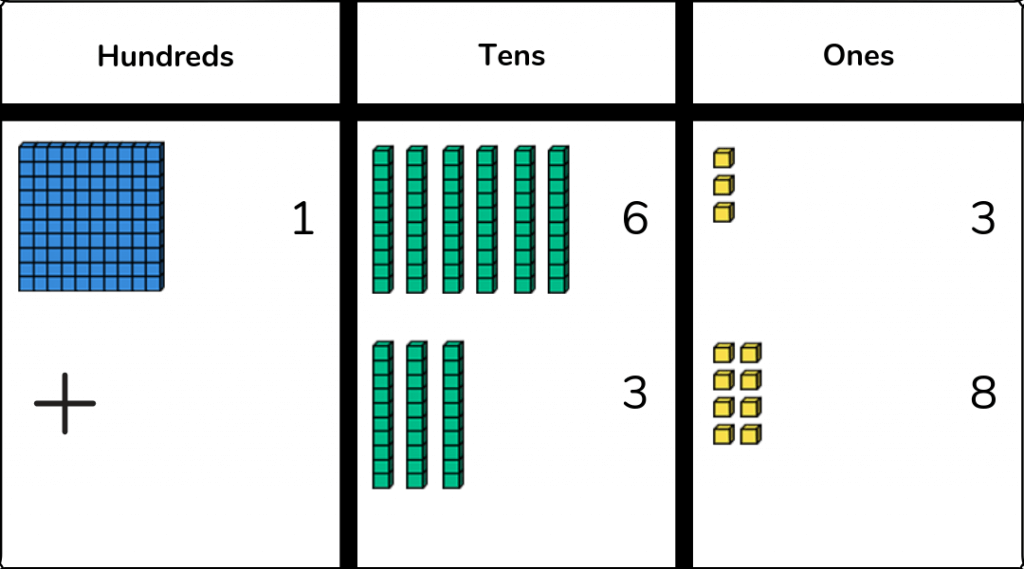
A basic example of the representational stage of column addition with base ten blocks.

Alongside the concrete resources children should be recording the numbers on the baseboard, and again have the opportunity to record representational representations.

Once children are completely secure with the value of digits and the base ten nature of our number system, base ten blocks can be replaced with place value counters. These help children as they progress towards the abstract, as unlike the base ten blocks, they are all the same size.

column addition example image — An example of counters as the intermediary between the concrete and abstract steps.

These should be introduced in the same way as the other resources, with children making use of a baseboard without regrouping initially, then progressing to calculations, which do involve regrouping.

As with the other equipment, children should have the opportunity to record the digits alongside the concrete resources and to progress to recording representationally once they are secure. The place value counters can be used to introduce children to larger numbers, calculating column addition involving the thousands and then the ten thousands column.

Teaching subtraction using the Concrete Representational Abstract

The method for teaching column subtraction is very similar to the method for column addition. Children should start by using familiar objects (such as straws) to make the 2-digit numbers, set out on a baseboard as column subtraction.

example image of column subtraction — The same lollipop sticks can now be used for subtraction.

To begin with, ensure the ones being subtracted don’t exceed those in the first number. Once children are confident with this concept, they can progress to calculations, which require exchanging. As with addition, the digits should be recorded alongside the concrete resources to ensure links are being built between the concrete and abstract.

Once secure with using the concrete resources, children should have the opportunity to record representationally, again recording the digits alongside.

As with addition, children should eventually progress to using formal mathematical equipment, such as base ten blocks.

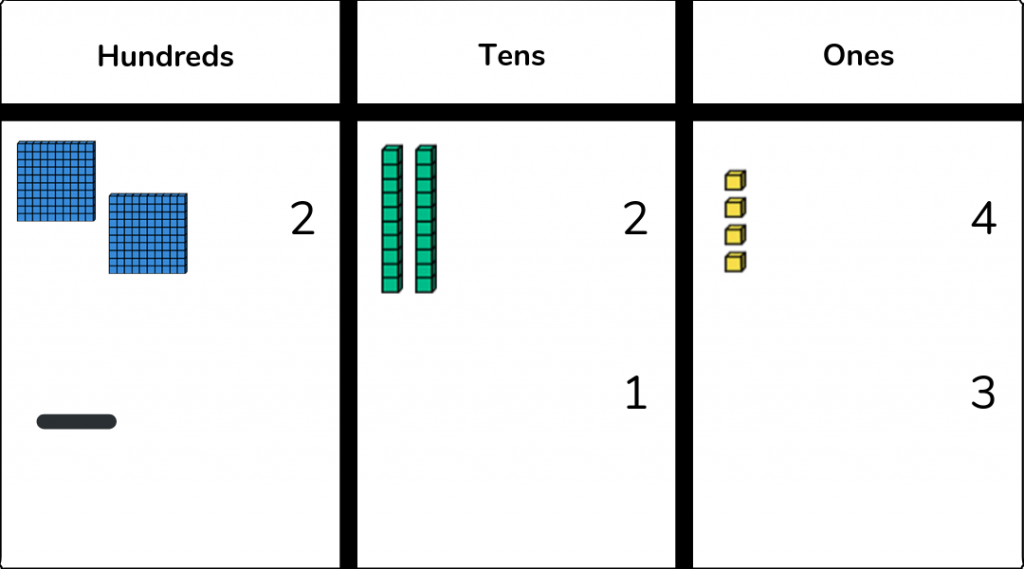
example image of column subtraction using dienes — An example of base ten blocks illustrating subtraction.

These should be introduced alongside the straws so students will make the link between the two resource types. Digits are noted down alongside the concrete resources and once secure in their understanding children can record the base ten blocks representationally, to ensure links are built between the concrete and abstract.

Once secure with the value of the digits using base ten blocks, children progress to using place value counters.

Column subtraction using place counters as concrete materials — Tackling subtraction using place value counters.

Again, the counters enable children to work concretely with larger numbers, as well as bridge the gap from the use of base ten blocks to the abstract. Along with the counters, children should be recording the digits and they should have the opportunity to record representationally once confident with the method using concrete resources.

Teaching multiplication using the Concrete Representational Abstract approach

The grid method is an important step in the teaching of multiplication, as it helps children to understand the concept of partitioning to multiply each digit separately.

Students can begin by drawing out the grid and representing the number being multiplied concretely. For example, 23 x 3 can be shown using straws, setting out 2 tens and 3 ones three times. This way, children can actually see what is happening when they multiply the tens and the ones.

multiplying straws grid method — Consistent object choices through the operations can assist a child’s learning process.

As with addition and subtraction, children should be recording the digits alongside the concrete apparatus, and recording representationally once they are confident with the concrete resources.

Children are then able to progress to representing the numbers in a grid, using place value counters.

Once children are confident using the counters, they can again record them representationally, ensuring they are writing the digits alongside both the concrete apparatus and the visual representations.

Progressing to the expanded method and then the short method of column multiplication is much easier for children if these are introduced alongside the grid method, to enable them to see the link.

Teaching division using the Concrete Representational Abstract (CRA) Approach

As children work towards the standard algorithm for division (long division), it is important they understand what is meant by both division as grouping and division as sharing.

Concrete resources are invaluable for representing this concept. Students need to understand how numbers can be partitioned and that each digit can be divided by both grouping and sharing.

partitioning with straws — In this example, the straws will be shared out between the stuffed toys.

Once confident using concrete resources (such as bundles of ten and individual straws, or base ten blocks), children can record them representationally, before progressing to more formal short division.

As children work towards understanding long division to find the quotient, concrete resources can be used to help them understand that 2-digit numbers can be partitioned and divided by both sharing and grouping. This can be through the use of bundles of ten straws and individual straws or base ten blocks to represent the tens and ones.

As with the other operations, it’s important that children are recording the digits alongside the concrete resources and are having the opportunity to draw visual representations. As children grow in confidence and once they are ready to progress to larger numbers, place value counters can replace the base ten blocks.

The Concrete Representational Abstract Approach is here to stay

It may have taken many years for CRA to reach the level of popularity it has today, but it is definitely here to stay.

I have seen firsthand how successful it can be when children have the opportunity to work in this way and I love the fact that children are now starting to have the conceptual understanding in math that I never had as a child.

Read more:

Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.

Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.

Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring

Why not learn more about how it works?

The content in this article was originally written by assistant headteacher Emma Johnson and has since been revised and adapted for US schools by elementary math teacher Katie Keeton.