Differentiation In The Classroom: The 8 Strategies That Will Support Every Student To Reach A Good Standard

The concept of differentiation in the classroom has had a bit of a bad rap recently as school leaders and teachers adopt a mastery approach to teaching. Here Neil Almond explains the 8 differentiation strategies that we should be using and how to make sure they’re used effectively in schools.

To start with, we’re dealing with a situation where there are so many bad differentiation strategies. It’s not hard when trying to implement differentiation in the classroom to fall into the trap of differentiating the wrong way, and widening the achievement gap we’ve been trying to close.

Add in that there are many other teaching strategies that provide similar benefits at much lower risk, and some teachers may simply feel that differentiation ‘isn’t worth it.’

But, using a mastery-based approach, it is possible, and ultimately essential, to develop a differentiated classroom that accommodates the individual needs of all students to create a learning experience that works for all.

Many of the ideas in this post are borrowed from Mark McCourt’s ‘Teaching For Mastery’ (see What is math mastery? and the Third Space guide to math mastery resources) and other sources.

The list of ways to differentiate in the classroom below should be a good starting point for you to continue your professional development and develop your whole class teaching in a more mastery-aligned way.

To start with, we need to be clear on some important language that is often used among educators, but whose meaning can vary between them. Below I shall outline what I mean by some of these words in the context of providing differentiated instruction. 

As an elementary math teacher and leader following a math mastery focused approach, many of the examples in this post will be math-based and focussed on the elementary classroom. The differentiation strategies I highlight can be used for any subject and any year group, however. 

Definitions of differentiation and differentiation strategies

What is differentiation?

Differentiation is often defined as tailoring instruction to meet the needs of individual students. However, this is too simplistic a definition in my view; we need to look at both what students’ needs might be through different prisms and how we can adjust our teaching and classroom management according to the ways they may present at different levels.

Differentiation in fluency 

When they first learn new mathematical concepts, students use much of their working memory to think about what they are being taught. 

We know from decades of cognitive science that our working memory – what we can think about in the moment and give attention to – is limited, some say between 4-7 pieces of information. 

That is why when we want to remember a telephone number we have to keep on repeating it so that it is not lost from our working memory and forgotten. 

Learning, as defined by Kirschner, Sweller and Clark, is a ‘change in long-term memory.’

Learners take what they hold in their working-memory and encode it into their long-term memory – a far more complicated process than I have made it sound here. 

From our long-term memory, we can call upon this information as needed with very little effort – multiplication facts are a good example – and transfer them to our working memory to solve problems. 

Fluency then, is the process of retrieving information from our long-term memory with no effort from our working memory, freeing up valuable space in our working memory to give attention to other things. 

Read more on cognitive load theory and fluency in math.

Differentiation of ability

When talking about ability, I am referring to an individual student’s capability to grasp new ideas and concepts. 

An ‘ability gap’ within a class will still be present whether that class is streamed or not. This is far from fixed, and changes in our pedagogy can result in students grasping new ideas more quickly and working at a higher level than they may have done previously. With the right learning opportunities, more students are able to become high achievers.

Differentiation of achievement

When talking about achievement, I am referring to the differences between what students in the class know. 

When we talk about ‘streaming’ classes – this is really what we mean. By setting students (or putting them into ability groups within classes), we are trying to limit the range of the achievement gap – the difference between the most that one student knows and the least another student knows – within classes. 

This then gives teachers and support staff a narrower range to focus on while giving high-quality instruction. 

It should be noted that in Mark’s book, he recognizes that there is no high-quality research into whether classes should be in mixed ability or set. 

Read more: Mixed ability vs ability grouping in elementary classrooms

Differentiation in the classroom as part of your teaching

With those important definitions established, let’s look at our list of ways to differentiate in the classroom that you could use to ensure your whole class is brought up to a good standard.

For the mastery model to work, groups need to be as highly homogenized as possible, meaning the achievement gap in a class needs to be as narrow as possible with the understanding that there would be great fluidity between groups.

Generally, however, this is out of the control of the teacher and is a strategic choice to be made by leaders. However, this does not mean a teacher cannot explore flexible grouping within their classroom environment.

Below you will find eight ways that a teacher can change their practice to ensure that, through their differentiation in teaching, everyone is brought up to a good standard.

In essence, these are the differentiated instruction strategies to aim for rather than different colored worksheets, different lesson plans, or different learning objectives.

List of differentiation strategies for the elementary school classroom

Differentiation Strategy 1: Teach with a mix of direct instruction and inquiry-based learning. 

A source of contention that ought to give those teachers with strong positive thoughts about inquiry-based learning a pause for thought. 

In order to give students the best chance to succeed (and bring all learners up together as one), the majority of our teaching should involve teacher-directed methods. 

The table below looks at how differentiated instruction impacted on PISA scores. 

While every teacher-directed method produced increases overall, inquiry-based methods had a negative impact when used with ‘none to few’ teacher-directed lessons. 

Most importantly, it is only when we use a mixture of teacher-directed methods and student centered learning inquiry-based learning that we optimize the benefits both methods can offer.

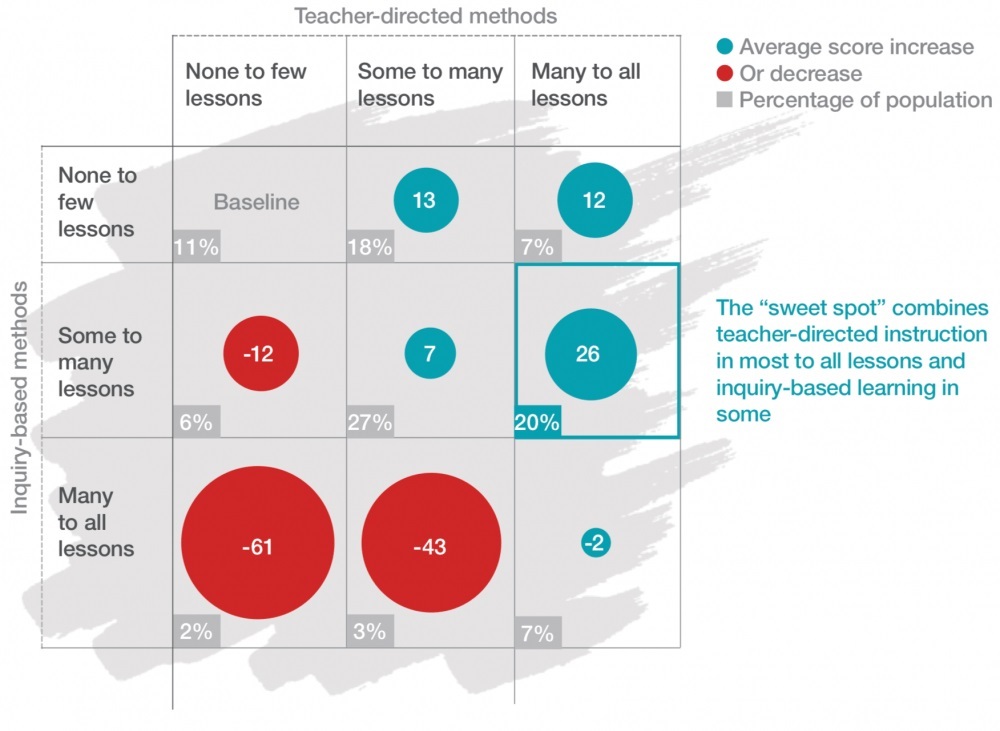
To ensure that the whole class is ‘brought up’ to the same level, it is crucial that we look at the pedagogical choices we make while teaching, and decide whether we’re making the most efficient choices to bring out the best in our students. 

One of the biggest variables in teaching for mastery is time; we need to use it wisely.  

When we can start with direct instruction for students about a topic, as opposed to having them discover it for themselves, we should.

Differentiation Strategy 2: Using manipulatives 

For those unfamiliar with the term, a manipulative is a physical object used to help teach a concept; they can be anything from fruits to blocks, as long as it enables a child to have a physical example of the concept being taught. They are commonly used as part of the Concrete Representational Abstract Approach. 

This is not to be confused with the idea of kinesthetic learning. The idea of ‘learning styles’ has been disproven, however, math manipulatives allow students who are learning new ideas to create mental representations of the subject being taught. 

Learning strategies such as mental representations help students embed conceptual understanding, increasing the chances that they will be able to apply these key concepts into other contexts. 

Interestingly, a study by Panasuk and Beyranevand (which McCourt cites in his book) claims that those who have deep conceptual understanding perform well on standardized tests, yet the opposite does not hold true. There is limited evidence to suggest that high achievement is a good indicator of deep conceptual understanding.

Manipulation of manipulatives, as well as articulating thoughts and ideas, can help to solidify ideas, concepts or facts and allow teachers to transfer this knowledge to new contexts. 

Mark McCourt, in his book ‘Teaching for Mastery,’ takes what he calls a ‘mathematical diversion’ and illustrates a range of ways in which he uses Cuisenaire rods to demonstrate a variety of mathematical ideas – including arithmetic with fractions and using negative numbers.

This is a great chapter in his book that ALL elementary school teachers should read and stick with.

Differentiation Strategy 3: Find gaps and fill them! 

The core purpose of mastery-based teaching is to ensure that no child is left behind.

In an ideal world, the route to mastery would have begun in kindergarten so the class group would be as homogenized as possible. 

Obviously, this will not be the case for those looking to begin to implement mastery principles in their current class. 

Where there is a large range of different abilities in a class, it is very unlikely that providing challenging and demanding work to the more able students at the top of the range and easier, less demanding work to those at the bottom of the range will decrease the achievement gap in any way. 

When differentiation is planned through giving students different tasks based on prior achievement, teachers are, in fact, increasing that gap.

To close the gap, elementary teachers should look to the first element of the mastery cycle and establish their students’ prior knowledge: what key ideas are missing from a child’s knowledge of a subject? Fill those gaps. 

This is when you should be creating or using diagnostic questions which are specifically designed on a range of mathematical content to identify a child’s misconceptions. Craig Barton’s Eedi website has been built around these.

Why knowledge gaps appear, and how to close them

As mentioned earlier, fluency is crucial for effective differentiation. For example, when students can remember their number facts and are fluent in number bonds to and within 10, the concept of place value, and multiplication facts, they can use a greater portion of their working memory to learn new math content. 

A child who is still reliant on using valuable working memory space to add numbers, perhaps with fingers, is likely to encounter cognitive overload when coupled with new instruction. 

This cognitive overload prevents new information from being encoded into the student’s long-term memory, meaning they are unlikely to reach their learning goals. 

A child who is confident in their number facts is able to recall this from their long-term memory, effectively bypassing the limits of working memory, and using their working memory to focus on the new content. 

Gap-filling can even be done “passively”; changing the displays in your classroom topic-by-topic is a great way of enriching students’ learning environment with knowledge that can fill gaps without conscious effort from the children. 

To help get everyone up to a good standard, ensure that there are plenty of opportunities for fluency and gap-filling. Have students quiz each other in pairs or small groups, chant times tables or mnemonics as a whole class – the greater the variety of classroom practices you can differentiate, the better!                

Read more: What Is A Spiral Curriculum: A Teacher’s Guide to What, How And When To Implement           

Differentiation Strategy 4: Prioritize learning over performance 

One of the most interesting findings from cognitive psychology over the last fifty years has been the distinction between performing well on a task and learning from that task. 

This finding has made the most profound change in my practice since I began my teaching career. 

Before, I would take students performing well on a task to be a good indication of students learning what I was teaching. It was always a massive frustration when in the next lesson (or in several lessons), I wanted the students to use that skill again and many were unable to recall it despite doing well in the original lesson. 

This is down to a simple concept that was lost to me during teacher training and the first four and a half years of my career – performing well and learning are two totally different things.

We’re always measuring how well students are performing; performance is the interactions they have with them ‘in the moment,’ or how many questions they got right on that worksheet. 

Yet performing well is a poor proxy for learning. It is easy to fall into the trap of ‘oh, the students have got this, let’s move on,’ because students are performing well. 

So when teachers move onto a topic too quickly based on performance, it is no wonder that the achievement gap increases. We’re essentially skipping part of the learning process, on the strength of incomplete evidence. 

To move everyone forward at the same pace, we need to ensure that concepts, facts and truths have been learned, not performed. 

Read more about how to prioritize learning over performance with our posts on metacognition in the classroom.

Differentiation Strategy 5: Use formative assessment to guarantee understanding

Formative assessment plays a massive role in bringing everyone up to the same standard. Especially in a class with diverse learning needs, awareness of the breadth of understanding between students is key to helping them improve.

Formative assessment crops up three times during the mastery cycle – at the beginning, element three, and element five.

1. Diagnostic pre-assessment with pre-teaching
2. High-quality, group-based initial instruction
3. Progress monitoring through regular formative assessment               
4. High-quality corrective instruction
5. Second, parallel formative assessment
6. Enrichment or extension activities

But what is formative assessment?

The purpose of formative assessment is to ascertain if the student has learned something and if they are understanding what is being taught. 

As educational psychologist David Ausubel put it in 1968, ‘The most important single factor influencing learning is what the learner already knows. Ascertain this and teach them accordingly.’

In Dylan Wiliam’s latest book, Creating the Schools our Children Need, he outlines five main features of short-cycle formative assessment and what teachers can do, minute-by-minute or day-by-day, to ensure high-quality formative assessment takes place.

1. Ensuring students know what they are meant to be learning
2. Finding out what the students have learned
3. Providing feedback that improves the students’ learning
4. Having students help each other learn (group work, peer marking, etc.)
5. Developing students’ ability to monitor and assess their own learning. 

The impact of formative assessment

Recent research has found that formative assessment has a positive effect on learning outcomes; the National Council of Teachers of Mathematics found that formative assessment produces greater increases in achievement and is more cost effective than other efforts to boost achievement such as reduced class sizes.

The other interesting thing they found was that students in the lower third for achievement showed greater progress than those in the highest third. 

Using assessment for learning can be used to establish what a student knows before teaching them something new, after we have taught them that new topic, and after we have changed our practice as a result of the first wave of formative assessment. This is one way that we can ensure everyone can be brought up to a high standard. 

For practical ideas on how to carry out the short-term formative assessment cycle, see Dylan Wiliam’s book, ‘Embedding Formative Assessment’ and Shirley Clarke’s ‘Outstanding Formative Assessment – Culture and Practice.’ 

Read more on formative vs summative assessment, questioning in the classroom strategies and the importance of a math diagnostic test for good teaching.

Differentiation Strategy 6: Create lessons with spaced practice

Spaced Practice refers to a specific practice concerned with timing – ‘when’ it’s best to learn.  

Is it better to spend seven hours on a Sunday to practice a skill before a test or to space those seven hours out to one hour sessions across seven days? 

Many studies have looked into this and the evidence is clear: it would be far better to practice seven one-hour sessions than to practice for seven hours the night before. 

Mark McCourt draws on the research of Rohrer and Taylor to illustrate this point. To summarize, three groups were asked to participate in a test and prepare for the test in the following ways:

	Week 1	Week 2	Week 3
Spacers	Two problems	Two problems	Test
Massers	Four problems	Test	Filler Task
Light Massers	Two problems	Test	Filler Task

The gap between practicing and taking the test was the same – one week. The final outcome was that those who used the spacing method of practice performed higher than the massed practice categories.

The implication for our teaching (if we want to take advantage of the benefits of spaced practice) is to dedicate some time in every lesson to go over previously learned material. Since January 2019, I begin all my math lessons the following way:

The last week, last month and last quarter structure proved a useful tool to space out practicing of core ideas across the school year that the students had already been taught. 

The students had to retrieve this information from their long-term memory; if they failed, this made it clear that the students had forgotten the idea, and so I could quickly adapt my lesson content to go over the content again.

I would also consider whether the homework I set should be based on recently taught content, or if it should be used to revisit previously taught content. 

Differentiation Strategy 7: Interleave effectively!

If spacing is to do with the ‘when’ of practice, interleaving is all about the ‘what.’ 

In an hour-long session, would it be better to spend the whole session practicing long division, or would it be better to practice fifteen minutes of long division and fifteen minutes of long multiplication twice over?  

Cognitive science is confident that the latter would provide the most benefits to long-term learning. 

Note that this should only be utilized once a skill has been taught. It would make very little sense to teach a day of fractions and a day of numbers and assume students can automatically work on them interchangeably. 

But once students are familiar with concepts, then the practicing of those concepts could be interleaved. 

The benefits of interleaving have been well documented, and Rohrer and Taylor again have produced math specific evidence of the benefits of interleaved practice. 

They found that those that interleaved their practicing two weeks before a test did not perform as well in their practice sessions as those who blocked work into one sitting. But they did score significantly higher than the blockers when it came to test performance, with the blockers achieving 20% accuracy and the interleavers scoring 63%. 

Interleaving is particularly useful in teaching the formal long division and long multiplication methods.

What does effective interleaving look like?

To help bring all students up to the same level, we should look to interleave new content with previously learnt material once we are sure it has been fully taught and understood. 

For example, if fractions have been taught, then that content could be interleaved into perimeter questions. 

Another way to interleave would be to put in several questions from a previously taught and unrelated topic into work that is being currently studied. 

If nothing else, this would ensure that children gain an awareness of the need to read questions carefully, and avoid going into auto-pilot when the same types of questions are repeated. 

Differentiation Strategy 8: Phased learning in the classroom

This is Mark McCourt’s proposed structure of a learning episode from Teaching For Mastery. 

In phased learning, there are 4 parts: Teach, Do, Practice, Behave. 

Phase 1: Teach

During the Teach phase, ideas are novel to the learner and the teacher will pass on key knowledge and facts through the use of worked examples, modeling and metaphor. This ensures that students are beginning to make new connections in their schema. 

Crucially, no new learning has taken place for the student. 

Phase 2: Do

The Do phase is to check if students have understood all the interaction and modeling from the Teach phase. 

The teacher is looking for replication of what has gone on previously. If not, the teacher can change their models and use high-quality corrective instruction personalized to individual learners to ensure that the students can grasp the idea. 

The other purpose of the Do phase is to build up a student’s confidence in a topic, so that they know they are able to learn the material at hand. Eagle-eyed readers will already be picking up on the crossover potential this has with the growth mindset.

Again no learning has happened by the end of this phase, just replication. 

Phase 3: Practice

The practice phase is when we seek to move students beyond mere performance, and provide the necessary conditions for far transfer – using concepts across different contexts. 

This can only be done when true fluency (as defined earlier) has been achieved and the students are able to use some of the space in their working memory to attend to the deeper structures of the idea. 

Phase 4: Behave

The final phase, which McCourt sees as the most important, is the Behave phase. It is here that learners are given the opportunity to demonstrate a deep understanding of the concept. 

The content we should expect the students to ‘Behave’ should not be the same content that was covered in the previous phases, but rather content already familiar with the students. 

As Mark McCourt puts it, ‘many teachers find it an uncomfortable – perhaps even illogical – process to plan the ‘Behave’ phase as one that relates to much earlier learning rather than the new idea, but it is crucial to do so if we want to bring about optimal gains in learning, understanding and long term recall.’ 

Differentiation in the classroom is a tool for long-term results

If we want all different students with different learning profiles to reach the same level, we need to put learning for the long-term ahead of short-term-gain performances by really looking at our teaching and redesigning it around the ideas and benefits of math mastery we’ve discussed here.

It’s further worth remembering that it will take time for the full impacts of differentiation in the classroom to be known. There may be some short-term improvements for different groups of students, but the real strength of mastery-based differentiation and other quality first teaching strategies is in the impact they can have across a child’s education.

With average diverse classrooms in the US containing students working at very different levels, already one teacher in a class of over 20 students at elementary and 25 at high school, students can struggle to close this achievement gap. However, working in small groups or one-to-one can have a significant impact on this. This is the reason Third Space continues to provide 1-to-1 math tutoring as the heart of our math intervention programs for elementary schools.   

Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.

Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.

Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring

Why not learn more about how it works?