Effective Questioning In The Classroom: 9 Tried and Tested Techniques For Teachers

April 23, 2024 | 5 min read

Pete Richardson

Effective questioning in the classroom can make or break your lesson. These questioning techniques are ones that I use time and again in my elementary school lessons; the questioning examples given are drawn from math but the principles apply across the curriculum.

I am an elementary teacher, but I’ve seen middle school and high school colleagues use similar questioning techniques in the classroom.

What is questioning in the classroom?

Effective questioning is an essential teaching skill that enables the educator to check students’ understanding, broaden and deepen the topic under discussion, and model clear thinking skills, and speaking and listening skills.

Why do we need effective questioning techniques in the classroom?

“Good learning starts with questions, not answers.” Guy Claxton, Professor in Education and Director of CLIO Development, University of Bristol.

And better questions tend to deepen and facilitate the learning process in the limited amount of time you have with your students, so let’s make the most of them.

Here are the top 3 reasons I believe in the importance of teacher questions.

First, if we remember our assessment to gain our teaching certifications, we will know that questioning in the classroom is a powerful formative assessment tool. Executed properly, higher order questions from the classroom teacher gives the teacher the opportunity to gauge student understanding of the topic as well as enabling students to actively participate in their own learning.
Second, a well thought out questioning strategy can help to build the relationship between teacher and student by encouraging engagement and improving verbal fluency of key concepts whether in elementary math or any other subject.
Third, good questions also lead to good class discussions, better student interactions, and ultimately, the shared understanding that is part and parcel of the learning experience.

See also: How To Learn Math

List of the 9 most effective classroom questioning techniques

This article will guide you through the 9 key questioning skills that, together with other teaching strategies, will have the most impact on your teaching and your classroom practice.

The majority of these 9 are open questions; they require longer, more thought out answers than those that only need a simple, short response (closed questions).

This means these types of questions usually won’t have either a correct answer or a wrong answer – an idea students may need some time to fully understand and accept.

1. Are you sure?

Developing students’ metacognition and critical thinking skills are crucial if we want them to be less reliant on the teacher as the person who ‘knows’.

If a student is used to asking a teacher ‘Is this right?’ and getting a response, then they are likely to not have checked their answer, not gained a deep enough understanding of the concept they are learning or have their need for affirmation so ingrained over years of schooling that they simply have to ask.

Asking ‘Are you sure?’ with a questioning tone will instantly flip the tables and create blind panic amongst your whole class. Especially when you ask the question as often when they are right as wrong. Even more so if you follow it up with ‘Well okay, if you are sure…’ or ‘If it makes sense to you…’

Now, obviously blind panic is not what we are aiming for, but it is a stage they will need to briefly enter until they get used to this and the other questions in the post.

Soon, especially if you encourage a growth mindset in your elementary school, they will pick up the idea that they really have to know if they are right or not and crucially, why. This leads us into a key follow-up question…

2. How do you know?

To be able to answer ‘Are you sure?’ confidently, students will need to have checked their calculation/explanation themselves, more and more often before they have even given their initial response.

Asking ‘How do you know?’ ensures this by asking them to share their reasoning with you, a group or the whole class.

This question is also a great way to really develop students’ thinking skills; they need to be clear not only that they have the right answer, but that they arrived at it by following the right method.

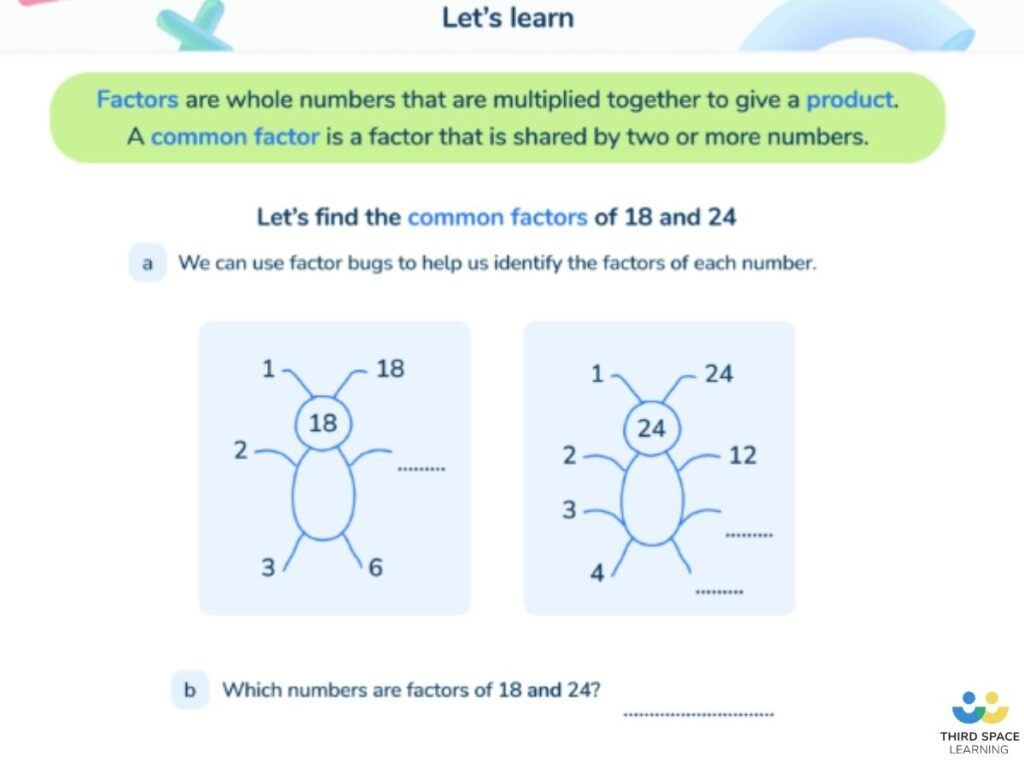
factors lesson slide — Taken from Third Space Learning’s online intervention lessons

The result of this increased metacognition is children will be more reliant on themselves (and each other) for checking their understanding, method and answer.

3. What do you notice?

Alongside metacognition, developing students’ ability to generalize can reap huge rewards. In other words, encouraging young learners to be mindful and look for patterns within and outside the mathematical area currently being learned. This also helps their number sense.

Asking students ‘What do you notice?’ when showing 2 calculations or problems at the same time can help children to see what is similar and different. It’s a key question when building procedural variation.

It also uncovers where a student’s understanding is, showing whether their current line of thinking is relevant to the current learning, in turn, enabling you to nudge them towards more relevant thinking where necessary.

In a lesson on exchanging you could ask the following question.

47 – 8 = 39

47 – 6 = 41

What do you notice about these two calculations?
This may yield answers such as:
- ‘8 and 6 are both even’ which are not particularly relevant,
- ‘the 4 and the 6 can be added to make 10’ shows up misconceptions
- ‘you don’t have enough ones (7) to subtract 8 but you do with 7-6’ which shows students are making relevant connections
From here it is a small step to ask for generalizations about subtracting ones from ones that can be applied whenever faced with that situation. eg ‘You must always regroup when you try and subtract more ones than you have.’

4. What’s the same and what’s different?

If you want a similar type of question that serves the same purpose as ‘What do you notice?’ but is more confining in its responses, asking ‘What’s the same and what’s different about these 2 calculations / problems / statements?’ will push that conversation on with you still guiding the direction.

5. Can you convince me?

This is another question that can help develop generalizations. Asking individuals or small groups to work together to convince you of something develops their depth of understanding and ability to reason.

Here are some math question examples:

‘Convince me that subtraction is the opposite of addition’
‘Convince me that all multiples of 8 are multiples of 2’

Flipping around the previous question’s example, ‘convince me that you always need to regroup when you subtract a 2 digit number (subtrahend) where the ones are greater than the initial number (minuend)’.

6. Is there another way?

‘Is there another way to find 25% of $80?’
‘Is there another way to work out 47 + 28?’
‘Is there another way you could have used to find all the possibilities?’

These kinds of questions help children who have not used a modeled or shared method realize they are not ‘wrong’ because their problem solving method is different (they may be less or more efficient).

It will also highlight to children that in Mathematics, as in life, there are many ways to approach something. It can also be used as a general challenge activity for students.

7. Is it always, sometimes, or never true?

This is a great higher-order thinking question to further develop children’s ability to generalize and, depending on the specific question used, their number sense. As with all the questions, it develops reasoning skills and can deepen student learning.

‘Is it always, sometimes or never true that you should round and adjust when you subtract 9 from a number?’

8. Can you imagine?

Building students’ ability to visualize things without actually doing it themselves helps in a number of disciplines such as Computing or Science, as well as mathematics.

Looking specifically at mathematics, it helps students understand and summarize problems and raises their ability to reason with a higher level of understanding.

So in a word problem, if you ask a student to imagine the train pulling up at that station at that time and then continuing on its journey to the next station, it can help contextualize an abstract time problem.

This type of questioning in the classroom is also a handy way to nudge children away from requiring concrete apparatus when you think they are ready, for example, ‘Can you imagine regrouping that ten for ten ones?’

9. I think I understand what you mean, are you saying?

Okay, so our final question is more of a leading question than an open-ended question, but it is still a very valuable tool. You will always find times where a student’s questions and ability to verbalize their reasoning is not quite at the same stage as their actual thinking and thought process.

Dependent on the situation and the student, you may find it supports them, your discussion or the pace of the lesson in general by reflecting on the student’s response by saying:

‘I think I understand what you mean, are you saying you would always round and adjust because you know that 9 will always be next to 10 so you will always be able to do the same adjustment afterwards?’

In other words, build on the student’s answer and reasoning, making it sharper or more concise so that the group or whole class can develop their understanding and the student giving the explanation can internalize their understanding further.

There are several variations on this question, such as:

‘You’ve really tried hard to explain that… are you saying…’ or
‘It’s a really difficult thing to explain, you’ve helped me understand it I think. Is this what you mean…’

So there you have it. Almost 9 questions that when used across school will significantly impact teaching and learning outcomes and ultimately, enable all students, high and low ability students, to achieve and use mathematics in their general lives.

Don’t rush the answers when questioning in the classroom!

One final piece of advice, if you’re new to these questioning strategies – think about how you’re going to be handling the answers to your questions too.

Give students thinking time, prompt them for when you’re looking for a long or a short answer, encourage the entire class to think about their own answers using their whiteboards to share their own thoughts.

These are the higher order skills from Bloom’s Taxonomy at work here, so it can take more time than usual. This is the learning process in action!