What Is A Bar Model And How Is It Used In Elementary School Math?
What is a bar model? The bar model method is a way to represent the underlying structures of mathematical problems to aid problem solving. The bar model is first introduced in 1st grade and then used more broadly across operations, according to Common Core, in upper elementary grade levels.
Many schools will use a ‘math mastery’ curriculum that prioritizes conceptual understanding over the rote memorization of mathematical facts and procedures. To do this, they will use what is known as a CRA approach – or the concrete representational abstract approach.
- What is a bar model?
- What is bar modeling
- How to explain a bar model to children
- When do students learn about bar models?
- Braces or bars in your bar models?
- How does a bar model relate to other areas of math?
- How does a bar model link to real life?
- Bar model examples
- Bar model practice questions and answers
The bar model is a useful tool as it can be demonstrated both in the concrete with actual math manipulatives (such as Cuisensaire rods or counters) but also through students’ drawings.
What is a bar model?
The bar model, also know as a strip diagram, is a pictorial representation of a math problem that uses rectangles to represent both known and unknown quantities (missing numbers). This may be used as the next stage after using concrete objects, such as blocks and counters.
Pre-K and elementary students can draw bars to represent values in math problems and when solving word problems. This can help them to answer the question more easily and can develop number sense.
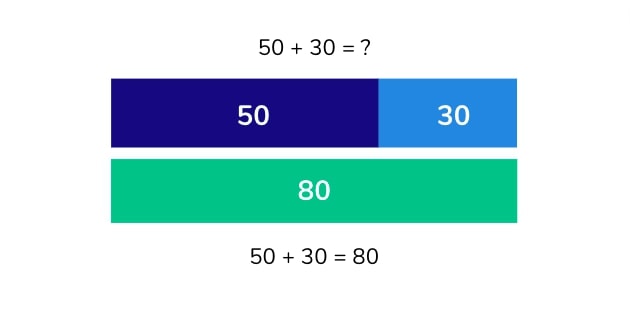
The bar model can be used across operations and math topics, but is particularly useful for multi-step problems and complex word problems.
The bar model is also known as the Singapore math model or the Singapore bar model.
What is bar modeling
Bar modeling uses blocks to represent values. The bar model is an effective, non concrete, way of helping your child and young mathematicians to understand numbers and values.
How to explain a bar model to children
We can explain the bar model to learners by taking a step by step Concrete Representational Abstract approach (also known as Concrete Pictorial Abstract). By first allowing students to use concrete objects such as counters, we can then transition them onto the representational bar model.
For example, by explaining that three counters represent the same amount as a bar model of three, we can help children to develop their number sense.
At Third Space Learning, we often use bar models in our elementary online math tutoring lessons. We use bar modeling to fill gaps in individual students’ learning and help to develop students’ solid understanding of mathematical concepts.

problem in a Third Space Learning online tutoring lesson
When do students learn about bar models?
Bar models are merely a way of representing problems and there is no requirement in the Common Core Math State Standards for them to be taught explicitly.
That said, many topics do encourage their use. Informal teaching of bar methods could begin in Kindergarten with the use of Cuisenaire rods and can move into more formal learning from 1st grade onwards.
Braces or bars in your bar models?
To represent the whole, some bar models will use a brace or another bar. The differences can be seen through the two models below.
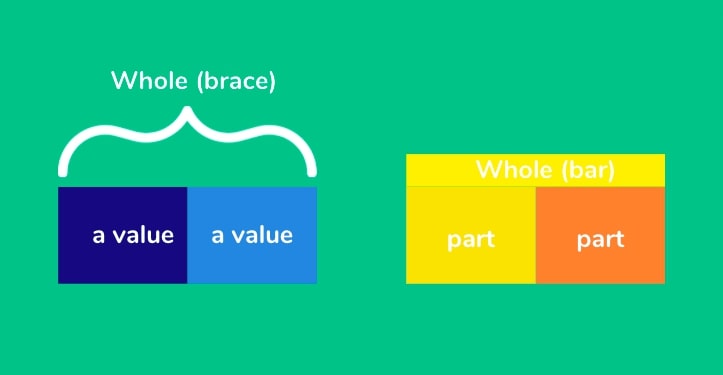
Having the whole represented by a bar is closer to what usually happens in concrete situations where a Cuisenaire rod of equal length is placed above the separate parts. Doing this in the early stages of bar modeling is advisable as it will help students move from concrete to representational.
However, as their understanding of the representations and underlying structures improves, it is beneficial to use a brace to represent the whole as it better represents the combination of the whole rather than a comparison model as can be seen when using the bar.
How does a bar model relate to other areas of math?
The bar model can be used for a wide variety of math number problems such as addition and subtraction problems and multiplication and division problems.
Use of bar models can help represent the mathematical structures of the 4 operations and can be used wherever word problems require the 4 operations. Therefore, bar models are unique in their flexibility within mathematics.
The bar model can also be used in math lessons to teach fractions and percentages. By using a fraction bar model, teachers can demonstrate the fractions and equal parts that make up one whole bar.

Bar models can also be used to help children understand what is place value.

How does a bar model link to real life?
The purpose of these models is to scaffold students’ understanding of numbers. It is therefore unnecessary for students to actually use these models in the real world.
However, the learning and understanding of numbers students will gain from using them early on in their mathematics journey will be stored as ‘mental models’ in which they can draw upon to solve the problems they encounter in ‘the real world’.
Bar model examples
Bar model example 1: addition
There were 19 people on the bus. Then 17 more people got on the bus. How many people are on the bus altogether?
The question tells us that there are 19 people on the bus. We can represent that using one bar.

We are then told that another 17 got on the bus. This can be demonstrated through the following:

The question asks us how many are now on the bus so this is an addition question.
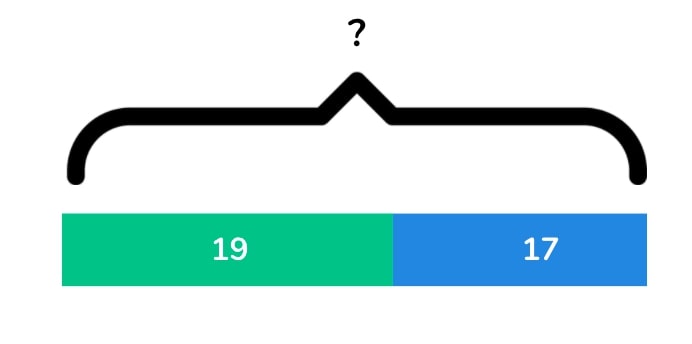
This is the final model for the question. 19 + 17 = 36. So the total number of people on the bus was 36.
Bar model example 2: multiplication as repeated addition
The length of one side of a square is 30cm. What is the perimeter?
To answer this question, we need to know that the perimeter is the length of the lines that make a shape. We also need to know that the length of the sides of a square are all equal and that there are 4 sides. If one side is 30 cm then the other sides will be 30 also. This would be 30 + 30 + 30 + 30 or 30 x 4.
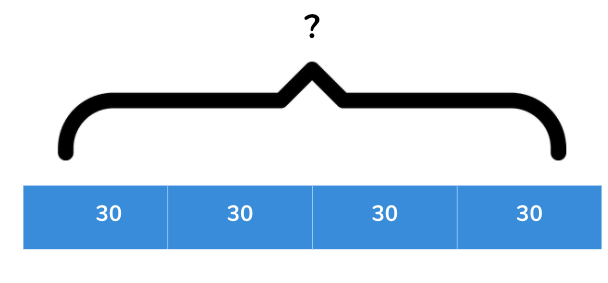
This is bar model multiplication as repeated addition. 30 x 4 can be thought of as 3 x 4 x 10 = 12 x 10 = 120cm.
Bar model example 3: inverse of multiplication structure
There is a total weight of 56 KG. Each weight is 7KG. How many weights are there altogether?
For this question, we know that there is a total weight of 56 kg and that each weight is 7 kg. What we do not know is how many weights there are in total. However, we know that there needs to be at least two – this first one and the last one that defines the end point.
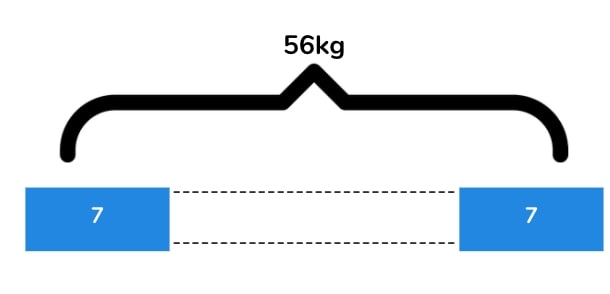
This is the inverse-of-multiplication structure and so what I need to be thinking about now is my knowledge of the 7 times table. 7, 14, 21, 18, 35, 42, 49, 56. 7 x 8 = 56 so there will be 8 weights altogether.
Bar model example 4: difference model of subtraction
I have 23 football cards and my friend has 17 football cards . How many more football cards do I have than my friend?
In this question, it is known that I have 23 football cards and that another person has 17. What it wants to know is how many more I have compared to the other. This can be shown using the bar model below.
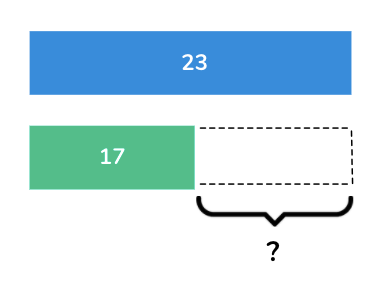
This is a difference model of subtraction and we can now solve the problem one of two ways. Either, we can subtract 17 from 23 or we can count on from 17 until we get to 23. This is down to student choice but the answer they should get is 6.
Bar model practice questions and answers
Use the bar models examples to represent the following problems.
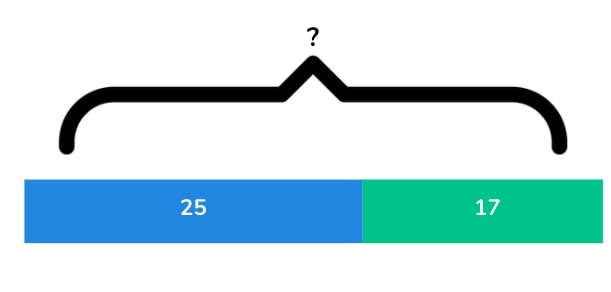
1. There were 25 people on the bus. Then 17 more people got on the bus. How many people are on the bus altogether?
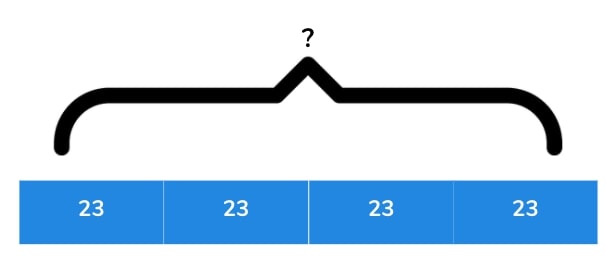
2. The length of one side of a square is 23cm. What is the perimeter?
3. There is a total weight of 40 KG. Each weight is 5KG. How many weights are there altogether?
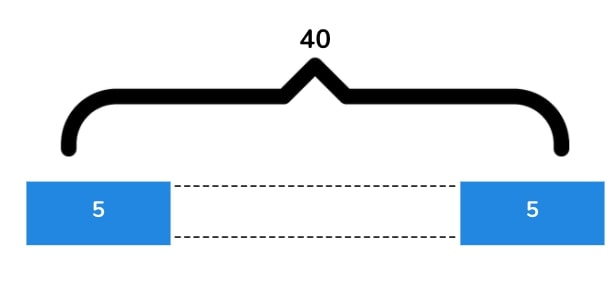
Answers:
- Augmentation
- Repeated addition
- Inverse-of-multiplication
What is an example of a bar model?
This image is an example of a bar model: a block representing a value.
What are the different types of bar models?
The different types of bar models are the part part whole model and the comparison model. In the part whole model, we usually know two parts and are trying to find the whole.
In the comparison model, we compare two different bars often looking at a before and after situation.
How do bar models solve word problems?
Bar models can help solve multi-step word problems by producing a visual of the problem. The visual representation can help students to understand wordy questions that may otherwise be difficult to comprehend.
Why is a bar model helpful?
A bar model helps students to visually see the information within a problem, often making it easier to understand.
Find out more about other elementary math vocabulary in our math dictionary for kids.
Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.
Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.
Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring
Why not learn more about how it works?
The content in this article was originally written by primary school lead teacher Neil Almond and has since been revised and adapted for US schools by elementary math teacher Christi Kulesza.




