Teaching Fractions: A Guide For Elementary School Teachers From 3rd Grade To 5th Grade

Fractions in upper elementary math not only extend students’ knowledge from lower elementary, but also act as the foundation from which several other topics – such as decimals and percentages – are developed.

Therefore, it’s essential to ensure your students approach them with confidence. This post will help you do exactly that, offering some practical suggestions as to how some objectives could be taught in the classroom.

When are fractions taught in elementary?

As anyone who has gone through the curriculum for math will know, the objectives related to fractions make up a large portion of the entire curriculum.

The teaching of fractions begins in 3rd grade where students are expected to find fractions of shapes and appropriate quantities. In 3rd grade, expectations in this domain are limited to fractions with denominators 2, 3, 4, 6, and 8.

Students compare simple fractions that have the same numerator or denominator by reasoning about their size. Finally, they must be aware that ²⁄₄, and ½ are equivalent.

As stressed in all the other blogs in this series, test the prerequisites and start from there. If students are unable to do the above, then it is unlikely they will be able to grasp fractions in 4th and 5th grade.

Fractions is usually a topic that fills some teachers with dread. I believe this to be because of three reasons: 

1. Fractions can be a difficult concept for the students to understand. It does not matter how many times a piece of paper is folded in half or into quarters, some students struggle to retain even this basic understanding.
2. Subject knowledge of fractions can be weak for some teachers who feel less confident due to their own experiences as a learner when grappling with fractions.
3. Low pedagogical content knowledge (how to teach a concept) can also be low for some teachers so they end up resorting to quick tricks and gimmicks (I am looking at you KCF – “keep it, change it, flip it”) to teach difficult concepts such as dividing fractions.
   
   This is usually the way the teacher was taught fractions and they would either understand the abstract immediately or be left to flounder and merely encode a procedure, with very little meaning, to long term memory.
   
   When students in the second category become teachers, they end up teaching these concepts to their students in a similar manner to how they were originally taught by their teachers. The cycle continues.

As professionals, we should be seeking out the opportunities available to us to improve our practice and break this cycle.

Introduction to Part and Whole of Numbers

A key step in students’ understanding of fractions is that they know early on that a fraction is not bound by a whole and has its own sense of ‘numberness’. Cuisenaire rods provide an excellent means of doing this. 

You could ask students to find half the purple rod.

They will quickly identify that red is half of the purple rod and place it like this, underneath the purple. 

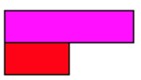
Ask them to find the other half of purple. Without difficulty students will be able to find another red rod and place it down.

The teacher could then place a white rod under the red and ask for the relationship between the white and the red. Probing questions such as ‘How many more white rods will I need to place down to be equivalent to a red rod?’ can be asked to move thinking forward.

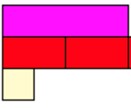
They will come to the conclusion that 1 white is half of a red, which is half of the purple. This can be continued until a train of 4 white rods are placed under the train of red rods.

We have now built up a representation that demonstrates how 1 whole is equivalent to 2 halves, which is equivalent to 4 quarters and the idea that a quarter is half of a half.

You can then have this written out as 1 = ²⁄₂ = ⁴⁄₄. Students should then be asked to make some conjectures. Hopefully seeing that when the denominator and numerator are equal, the fractions are equivalent to one whole. 

Next, we could ask students to place another half of purple down. Here the rods have a distinct advantage over commonly used visual representations, such as circles to represent pizzas.

If we use pizza, and we ask students to get another half of a pizza, they could turn around, quite rightly, and claim that it cannot be done as there is no more pizza left.

With rods, a child can easily understand that by adding another half, they would need to collect another red rod and place it at the end of the train of red rods, like so. 

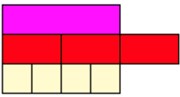
Now the students can understand that a fraction can denote a number >1. You may now wish to get students to conjecture how many more quarters are needed to be equivalent to three halves.

They will see either through using more rods or identifying the pattern previously, that 2 more white rods (quarters) will be needed.

Teachers could now write that ³⁄₂r = ⁶⁄₄w. Finally, you could ask students to find just one other rod that is equivalent to ³⁄₂r = ⁶⁄₄w. After some experimenting, they will be able to place a light green rod under the train of white rods.

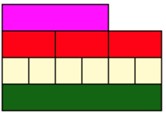
We can now express that 1lg = ³⁄₂r = ⁶⁄₄w. 

Fractions 3rd grade

• Understand a fraction as the quantity formed by 1 part when a whole is partitioned into equal parts.
• Understand a fraction as a number on the number line; represent fractions on a number line diagram.
• Explain equivalence of fractions in special cases, and compare fractions by reasoning about their size.
  • Understand two fractions as equivalent (equal) if they are the same size, or the same point on a number line.
  • Recognize and generate simple equivalent fractions, e.g., 1/2 = 2/4, 4/6 = 2/3. Explain why the fractions are equivalent, e.g., by using a visual fraction model.
  • Express whole numbers as fractions, and recognize fractions that are equivalent to whole numbers. Examples: Express 3 in the form 3 = 3/1; recognize that 6/1 = 6; locate 4/4 and 1 at the same point of a number line diagram.
  • Compare two fractions with the same numerator or the same denominator by reasoning about their size. Recognize that comparisons are valid only when the two fractions refer to the same whole. Record the results of comparisons with the symbols >, =, or <.

Fractions activities 3rd grade

Focus on the following objectives:

• Understand two fractions as equivalent (equal) if they are the same size, or the same point on a number line.
• Recognize and generate simple equivalent fractions, e.g., 1/2 = 2/4, 4/6 = 2/3. Explain why the fractions are equivalent, e.g., by using a visual fraction model.

When looking at equivalent fractions, using fraction walls should be your first pedagogical choice. Every child should have one and, in an ideal world, know not to touch and fiddle with the pieces until you have told them to.

If you know students are not capable of this, it is best to let them have a play with them first and see what they produce. This always provides some interesting discussion points if you are observing what the students do and notice. 

In 3rd grade, standards are limited to fractions with denominators 2, 3, 4, 6, and 8.

Explain what is meant by equivalent fractions. Here, students can use their knowledge of the words to see ‘equivalent’ begins with a word similar to equal which means ‘the same’ and fractions they know means ‘a break’.

So equivalent fractions are breaks which are the same.

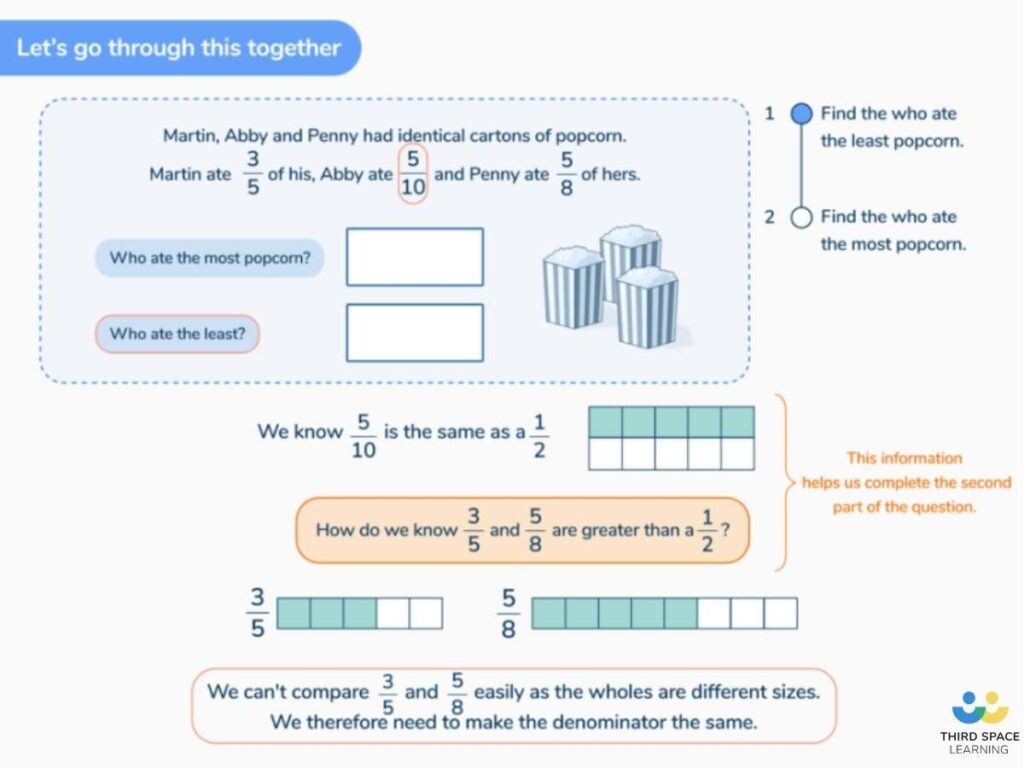
Begin by asking the students to get ½ from their fraction wall.

Ask students to place down the thirds and ask can you place the thirds underneath the ½ so that the total length of both bars are the same length. They will soon realize that they are not able to do this. Write ⅓ on the board. 

Move onto quarters and ask them to do the same as with the thirds. It is important that students can see how the two blue blocks representing ¼ each is the same as ²⁄₄. They will tell you that it can be done and that ²⁄₄ are the same as ½. 

Write down ²⁄₄ on the board in a separate area from ⅓. Ask if they can do the same with fifths.  Again, they will find out that you cannot find an equivalent fraction of ½ with fifths. Write ⅕ on the board next to ⅓.

Ask them if it can be done with sixths. Very quickly the students will realize that it can be and they will have the following:

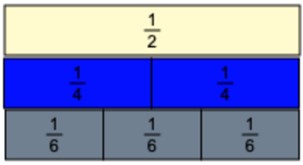
Write ³⁄₆ on the board where you have written ½ and ²⁄₄. 

Repeat the above until you have gone through all the denominators through to 8. They will have the following:

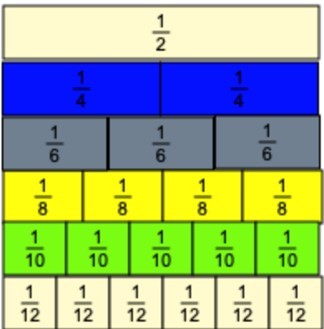
And on your board you should have:

½, ²⁄₄, ³⁄₆, and ⁴⁄₈ together and ⅓ and ⅕ together.

From here, you need to be directing and probing students’ thinking so that they can make some conjectures. Can they see that within the equivalent fractions for ½ that the numerator and denominator are both even numbers? Do they see that the numerator is half the denominator?

What conjectures can they make from this? Would ³⁸⁄₇₆ therefore be equivalent to one half?  And for the numbers on the other side, what can they deduce from that? Ah, when the denominators are odd then an equivalent fraction to ½ cannot be made through a fractional representation. 

You could then guide and ask students to find other fractional equivalents for other fractions. 

It is important to remember that we want the students to think; not just placing different parts of the fraction wall down in a ‘have a go’ way. So asking students to conjecture each time they have found the fractional equivalents is so important.

For 1/4 we would expect students to notice that only when a denominator is in the 4 times table will it contain an equivalent fraction.

The focus and outcome of this lesson should always be for students to begin making these types of conjectures not to play around and build up the fraction wall.

When teaching, you need to ensure that that is at the forefront of your mind. Carefully planned questions are key here. 

Fractions word problems 3rd grade

A typical word problem could be the following:

I know that ²⁄₄ is the same as ²⁄₂ because the numerators are the same. Is this statement correct or incorrect? Explain why.

Students could draw bars in their book to demonstrate this:

Or explain that when the numerators are the same, the larger the denominator the smaller the fraction.

Fractions: reasoning and problem solving

A reasoning activity could be the following:

Using the numerals 1, 2, 3, 4, 6, and 8 find all the equivalent fractions. 

This is where all that conjecturing done previously can come into play. The more of that the students have done, the more mathematical their approach to solving this would be.

They will not need to use trial and error with the support of a fraction wall, rather they can use what they know about the underlying relationships of fractions and equivalence. That said, ensuring that fraction walls are available to support learners is important.

You would expect students to find the following:

½ = ²⁄₄ = ⁴⁄₈ 

¼ = ²⁄₈

⅔ = 4/6 

¾ = 6/8 

Fraction walls 3rd grade

A popular approach to teaching fractions in this year is to use a fraction wall, pictured below:

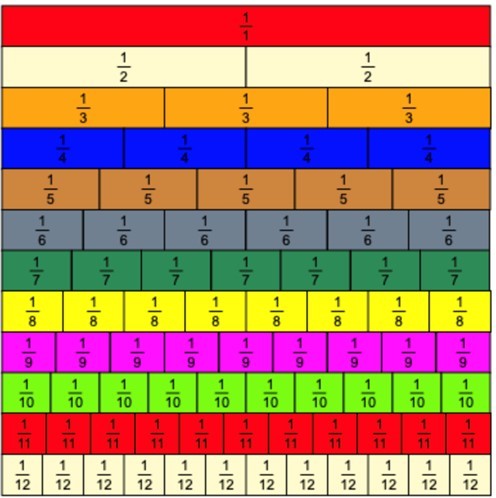
The fraction wall works in a slightly different way to Cuisenaire rods as I am sure you can see. While the rods help us see the numberness found within fractions, the fraction wall helps us to see that we can break one whole into many equal parts without being hindered by the physical size of the rod. 

For example, it is impossible to demonstrate that ³⁄₃ is equivalent to ¹⁄₁ using Cuisenaire rods as the length of the rods would not match the value of the whole.

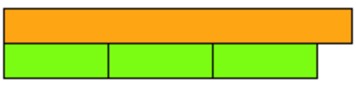
If I swapped out the value of the whole from the orange to the blue, we would then see that there are no 2 rods that could make the length of the blue.

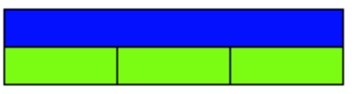
Here we can see that, in an attempt to represent ½, that the yellow rods are physically too big while the purple rods are physically too small. 

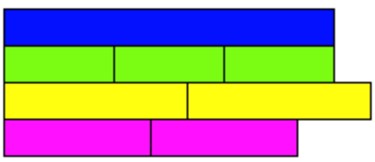
We are therefore left with no choice other than to select the fraction wall.

Note that the complete fraction wall shown above goes up to a denominator of 12, but 3rd grade is limited to denominators up to 8.

Fractions 4th grade

• Explain why a fraction a/b is equivalent to a fraction (n × a)/(n × b) by using visual fraction models; recognize and generate equivalent fractions.
• Compare two fractions with different numerators and different denominators, e.g., by creating common denominators or numerators, or by comparing to a benchmark fraction such as 1/2.; Record the results of comparisons with symbols >, =, or <.
• Understand a fraction a/b with a > 1 as a sum of fractions 1/b.
  • Understand addition and subtraction of fractions as joining and separating parts referring to the same whole.
  • Decompose a fraction into a sum of fractions with the same denominator in more than one way, recording each decomposition by an equation. Justify decompositions, e.g., by using a visual fraction model
    Examples: 3/8 = 1/8 + 1/8 + 1/8 ; 3/8 = 1/8 + 2/8 ; 2 1/8 = 1 + 1 + 1/8 = 8/8 + 8/8 + 1/8.
    
  • Add and subtract mixed numbers with like denominators, e.g., by replacing each mixed number with an equivalent fraction, and/or by using properties of operations and the relationship between addition and subtraction.
  • Solve word problems involving addition and subtraction of fractions referring to the same whole and having like denominators, e.g., by using visual fraction models and equations to represent the problem.
• Apply and extend previous understandings of multiplication to multiply a fraction by a whole number.
  • Understand a fraction a/b as a multiple of 1/b.
    For example, use a visual fraction model to represent 5/4 as the product 5 × (1/4), recording the conclusion by the equation 5/4 = 5 × (1/4).
    
  • Understand a multiple of a/b as a multiple of 1/b, and use this understanding to multiply a fraction by a whole number.
    For example, use a visual fraction model to express 3 × (2/5) as 6 × (1/5), recognizing this product as 6/5. (In general, n × (a/b) = (n × a)/b.)
    
  • Solve word problems involving multiplication of a fraction by a whole number, e.g., by using visual fraction models and equations to represent the problem.
    For example, if each person at a party will eat 3/8 of a pound of roast beef, and there will be 5 people at the party, how many pounds of roast beef will be needed? Between what two whole numbers does your answer lie?
• Express a fraction with denominator 10 as an equivalent fraction with denominator 100, and use this technique to add two fractions with respective denominators 10 and 100.
  For example, express 3/10 as 30/100, and add 3/10 + 4/100 = 34/100.
  
• Use decimal notation for fractions with denominators 10 or 100.
  For example, rewrite 0.62 as 62/100; describe a length as 0.62 meters; locate 0.62 on a number line diagram.
  
• Compare two decimals to hundredths by reasoning about their size. Recognize that comparisons are valid only when the two decimals refer to the same whole. Record the results of comparisons with the symbols >, =, or <, and justify the conclusions, e.g., by using a visual model.

Fractions activities 4th grade

For this lesson, address the following objective:

• Apply and extend previous understandings of multiplication to multiply a fraction by a whole number.
  • Understand a fraction a/b as a multiple of 1/b.
  • Understand a multiple of a/b as a multiple of 1/b, and use this understanding to multiply a fraction by a whole number. 
  • Solve word problems involving multiplication of a fraction by a whole number, e.g., by using visual fraction models and equations to represent the problem. 

When introducing multiplication with fractions, care needs to be given into how they are presented to the students. For example, 3 multiplied by ⅖ is difficult to visualize. But saying 3 groups of ⅖ helps us to see that we need to have 2/5 three times.

Reminding students that multiplication is also repeated addition is a key part here. Rewriting the question as ⅖ + ⅖ + ⅖ = is helpful too. 

In terms of using manipulatives, I believe it is best to use Cuisenaire rods to demonstrate how to do this. Below, I will detail how I would model this.

The orange rod represents our whole. We need to find which rod would represent a fifth.

Students should know that 5/5 makes one whole so they need to find a rod that can be laid 5 times so that it is equal in length to the whole.

It may be the case that students now instinctively know by this stage that the red rod represents 1/5. It is important that they lay 2 of the these to represent ⅖.

The next question we should ask will be, is there a rod that is equivalent to ⅖? Students may need some time to do this but through experimentation they will see that the purple rod can be one rod that represents ⅖. 

At this point, ask the students to remove the 2 red blocks reminding them this block represents ⅖.

Refer back to the question of 3 x ⅖. Remind students that we need 3 groups of ⅖ and that if we have one group already we will need 2 more groups.

Tell students to place 2 more purple rods next to the first one. They should have the following:

Ask students how many fifths we now have, reminding them that each purple block was worth ⅖. They will be able to count that there are ⁶⁄₅ altogether. Some students will be able to convert this to a mixed fraction.

For those that cannot, ask them to place red blocks the length of the purple train, reminding them that red blocks here represent ⅕. 

The students will have placed 6 red rods down. Ask the students if there are any rods that go further than the length of the whole and to move that number of rods and place them next to the whole.

They should then have the following:

From here you can guide them in seeing that at the top train we have one whole and ⅕. So ⁶⁄₅ as a mixed fraction would be 1 ⅕.

Of course, it is then important to ensure that you get students to practice this with other questions using the I do, we do, you do approach.

If using rods is new to you, then pre-planning these in advance and being absolutely clear in what you will do with the rods and the questions you will ask is crucial. 

Fractions word problems 4th grade

With novel content, it is best to keep the word problems simple and with numbers that students can understand. An appropriate word problem might be something like:

Amy is having a party with 3 other friends. Each person will eat ¾ of a pizza, how many pizzas will they need altogether?

First to note is that in total there are 4 people in total. Amy and 3 friends. The equation will be 4 x ¾.

When using rods to demonstrate this, it is important to select a rod that can be split into four equal parts. The brown rod allows for this. 

The process then follows much the same as the previous example. Find the rods that denote ¼ and place three of them down. 

The brown rod represents one whole pizza and the red rods (¾  of the total length) show how much each person intends to eat. Find a rod with the same value as the three red trains and place this down instead of the three red rods. This will be the dark green rod.

Remind students that 4 people will eat ¾ of a pizza, so we need 3 more dark green rods. Get the students to place them down.

Remind students that the brown rod represents one whole pizza and the total train of dark green rods, the total amount of pizza that will be consumed.

Therefore, we need to place brown rods down until they are equal or just greater than the length of the dark green train. When students do this, they will get:

As each brown rod represents a whole pizza, it can be determined that 3 whole pizzas would be required. 

Fractions: reasoning and problem solving

As this is novel content, using it to see if students have misconceptions would be the best use of reasoning.

⅘ x 3 = ¹²⁄₁₅. Is this the correct answer? Explain why.

Here we are expecting the students to notice that the denominator has been multiplied by the whole number and so the answer would be incorrect as the denominator does not change. 

The correct answer would be ¹²⁄₅ or 2 and ⅖

Fractions 5th grade

• Add and subtract fractions with unlike denominators (including mixed numbers) by replacing given fractions with equivalent fractions in such a way as to produce an equivalent sum or difference of fractions with like denominators.
  
  For example, 2/3 + 5/4 = 8/12 + 15/12 = 23/12. (In general, a/b + c/d = (ad + bc)/bd.)
  
• Solve word problems involving addition and subtraction of fractions referring to the same whole, including cases of unlike denominators, e.g., by using visual fraction models or equations to represent the problem.
  
  Use benchmark fractions and number sense of fractions to estimate mentally and assess the reasonableness of answers. For example, recognize an incorrect result 2/5 + 1/2 = 3/7, by observing that 3/7 < 1/2.
  
• Interpret a fraction as division of the numerator by the denominator (a/b = a ÷ b). Solve word problems involving division of whole numbers leading to answers in the form of fractions or mixed numbers, e.g., by using visual fraction models or equations to represent the problem.
  
  For example, interpret 3/4 as the result of dividing 3 by 4, noting that 3/4 multiplied by 4 equals 3, and that when 3 wholes are shared equally among 4 people each person has a share of size 3/4.
  
  If 9 people want to share a 50-pound sack of rice equally by weight, how many pounds of rice should each person get? Between what two whole numbers does your answer lie?
  
• Apply and extend previous understandings of multiplication to multiply a fraction or whole number by a fraction.
  • Interpret the product (a/b) × q as a parts of a partition of q into b equal parts; equivalently, as the result of a sequence of operations a × q ÷ b.
    For example, use a visual fraction model to show (2/3) × 4 = 8/3, and create a story context for this equation. Do the same with (2/3) × (4/5) = 8/15. (In general, (a/b) × (c/d) = (ac)/(bd).
    
  • Find the area of a rectangle with fractional side lengths by tiling it with unit squares of the appropriate unit fraction side lengths, and show that the area is the same as would be found by multiplying the side lengths.
    
    Multiply fractional side lengths to find areas of rectangles, and represent fraction products as rectangular areas.
    
• Interpret multiplication as scaling (resizing), by:
  • Comparing the size of a product to the size of one factor on the basis of the size of the other factor, without performing the indicated multiplication.
  • Explaining why multiplying a given number by a fraction greater than 1 results in a product greater than the given number (recognizing multiplication by whole numbers greater than 1 as a familiar case); explaining why multiplying a given number by a fraction less than 1 results in a product smaller than the given number; and relating the principle of fraction equivalence a/b = (n × a)/(n × b) to the effect of multiplying a/b by 1.
• Solve real world problems involving multiplication of fractions and mixed numbers, e.g., by using visual fraction models or equations to represent the problem.
• Apply and extend previous understandings of division to divide unit fractions by whole numbers and whole numbers by unit fractions.
  • Interpret division of a unit fraction by a non-zero whole number, and compute such quotients.
    For example, create a story context for (1/3) ÷ 4, and use a visual fraction model to show the quotient. Use the relationship between multiplication and division to explain that (1/3) ÷ 4 = 1/12 because (1/12) × 4 = 1/3.
    
  • Interpret division of a whole number by a unit fraction, and compute such quotients.
    For example, create a story context for 4 ÷ (1/5), and use a visual fraction model to show the quotient. Use the relationship between multiplication and division to explain that 4 ÷ (1/5) = 20 because 20 × (1/5) = 4.
    
  • Solve real world problems involving division of unit fractions by non-zero whole numbers and division of whole numbers by unit fractions, e.g., by using visual fraction models and equations to represent the problem.
    For example, how much chocolate will each person get if 3 people share 1/2 lb of chocolate equally? How many 1/3-cup servings are in 2 cups of raisins?

Fractions lesson ideas 5th grade

For this lesson, focus on the following objective:

• Apply and extend previous understandings of multiplication to multiply a fraction or whole number by a fraction.

This can be taught through simple algorithmic ways – multiply the numerators together; then multiply the denominators together; and finally write the fraction.

But it can give very little conceptual understanding and fails to explain really why multiplying gives an answer that is smaller than the other two fractions.

Much of a student’s experience has been that multiplication makes something bigger, when this is evidently not true. 

We will deal with the equation ¼ x ½  = ?

Teachers need to make careful pedagogical choices as to how they are going to pronounce this question. One fourth multiplied by one half invokes the area model of multiplication and this is what I will focus this on.

By this point, I am assuming that the students have had some prior knowledge working with rods. 

First, we need to guide students through finding the unit whole. As the fractions we are multiplying are  ¼ and ½, we want students to make an informed choice by choosing a rod that can be split equally into halves and quarters. As shown below, the brown rod allows for this to happen:

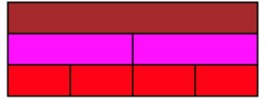
Next, we guide students into setting up the area model. We remind students that the unit whole is a brown rod and so the trains of the red rods and purple rods must equal the length of the brown rods.

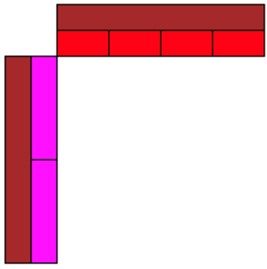
Here we check for understanding. Are students clear that the purple rods represent one half and the red rods represent one fourth? If not, then this needs to be reinforced.

As each side has a unit length of one whole, students now need to understand that the whole area created by the vertical and horizontal rods is equal to 1 x 1.

In my experience, this is something that students struggle with the most and so it is worth spending some time looking at this.

The shaded area below demonstrates this. That shaded area has a total value of 1.

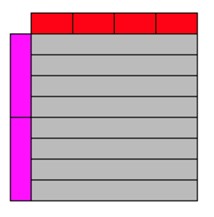
As we are looking at ¼ x ½, we only need to fill the area where one quarter and one half intersect. Which would be this.

Students can either use the red rods or the purple rods to complete the area of just one of the ½ rods and one of ¼ rods. Guide the students to this conclusion.

What is now important is to direct a student’s attention to the fact that from the area you have covered (the two purple rods you have just placed) you would need to replicate that eight more times to cover the whole area (see below). 

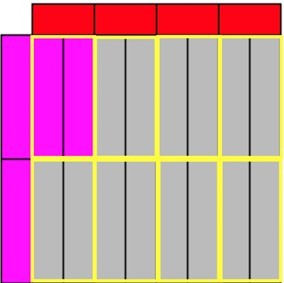
Remind students that the total area would be equal to one for the reasons set out above. Therefore, the two purple rods would need to be replicated 8 times to fill the area but presently, it only covers up one part. The model shows that ¼ x ½  = ⅛.

Fractions word problems 5th grade

 A suitable problem might be the following:

There was ⅝ of a pie left in the fridge. Daniel ate ¼ of the leftover pie. How much of a pie did he have?

Students could represent that problem like this. 

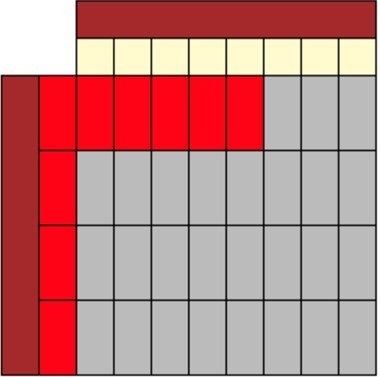
They would be able to see that there are 32 parts all together and they laid 5 red rods down. Therefore, Dan has consumed ⁵⁄₃₂ of the leftover pie. 

Fractions: reasoning and problem solving

A suitable problem for 5th graders might be the following:

⅔ x ¾ is the same as ¾ of ⅔. Prove it. 

Students may create the following to prove that they are the same. The total area that is covered by each representation is 6 out of the 12 possible parts, making the answer ½.

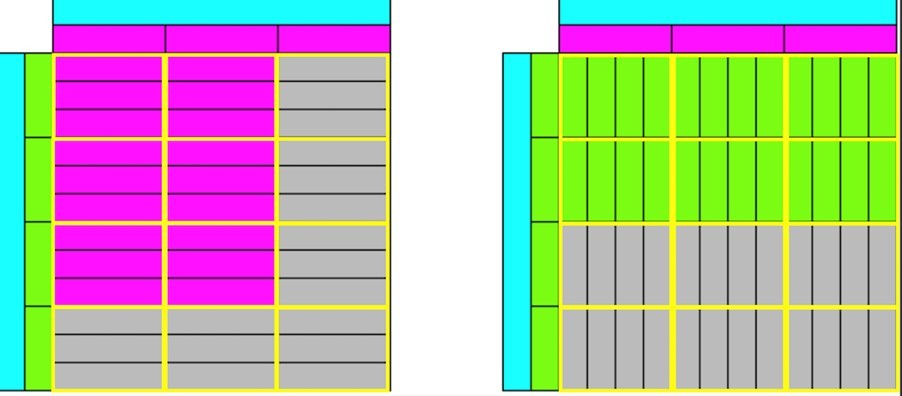
However, they can also rely on their knowledge of the Commutative Property which always holds true for multiplication which is the following:

A x B = C and B x A = C

Whichever way you choose to multiply the numbers, you will always get the same answer.

Fractions is one of the most important topics in common core elementary math, and confidence in it is the key to succeeding at many other math topics. Hopefully this post has shown you some ways to help your students achieve that confidence!

Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.

Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.

Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring

Why not learn more about how it works?

The content in this article was originally written by primary school lead teacher Neil Almond and has since been revised and adapted for US schools by elementary math teacher Katie Keeton.