What Is A Non-unit Fraction: Explained For Teachers, Parents And Kids

Fractions are taught right from early years, beginning with proper fractions (unit and non-unit) and progressing to improper fractions.

What is a non-unit fraction?

Whereas a unit fraction is one part of a whole (the numerator is always 1 i.e.  ½, 1⁄7 or 1⁄376. ), a non-unit fraction is a fraction with a numerator (top number) greater than 1. 

Non-unit fractions could be proper fractions (less than 1 whole, where the denominator (bottom number) is larger than the numerator) or improper fractions.

Examples of non-unit fractions

⅔, 6⁄11 and 29⁄100 are examples of non-unit fractions that are proper (less than 1 whole).

5⁄5, 12⁄12 and 86⁄86 are examples of non-unit fractions that are equal to 1 whole.

7⁄6, 13⁄9 and 48⁄13 are examples of non-unit fractions that are improper (more than 1 whole).

4⁄2, 9⁄3 and 20⁄4 are examples of non-unit fractions that are equal to an integer (whole number). 

When do children learn about non-unit fractions in elementary school?

Children will first encounter non-unit fractions in 3rd grade math lessons – namely 2⁄4 and ¾. They are introduced to ½ and ¼, which is then followed by ⅓, 2⁄4 and ¾. Non-unit fractions are prevalent thereafter in the curriculum. 

How do non-unit fractions relate to other areas of math?

Non-unit fractions can be found in any area of math that involves a quantity of some sort. 

Non-unit fractions in real life

As above, non-unit fractions can be used in any context that involves a quantity, e.g. ¾ of an hour; ⅔ of the class; ⅘ of a liter, etc.

3 worked examples for non-unit fractions

Many fraction questions can be visually demonstrated with the use of bar models (as shown below), number lines, or other similar diagrams that can be clearly split into equal parts.

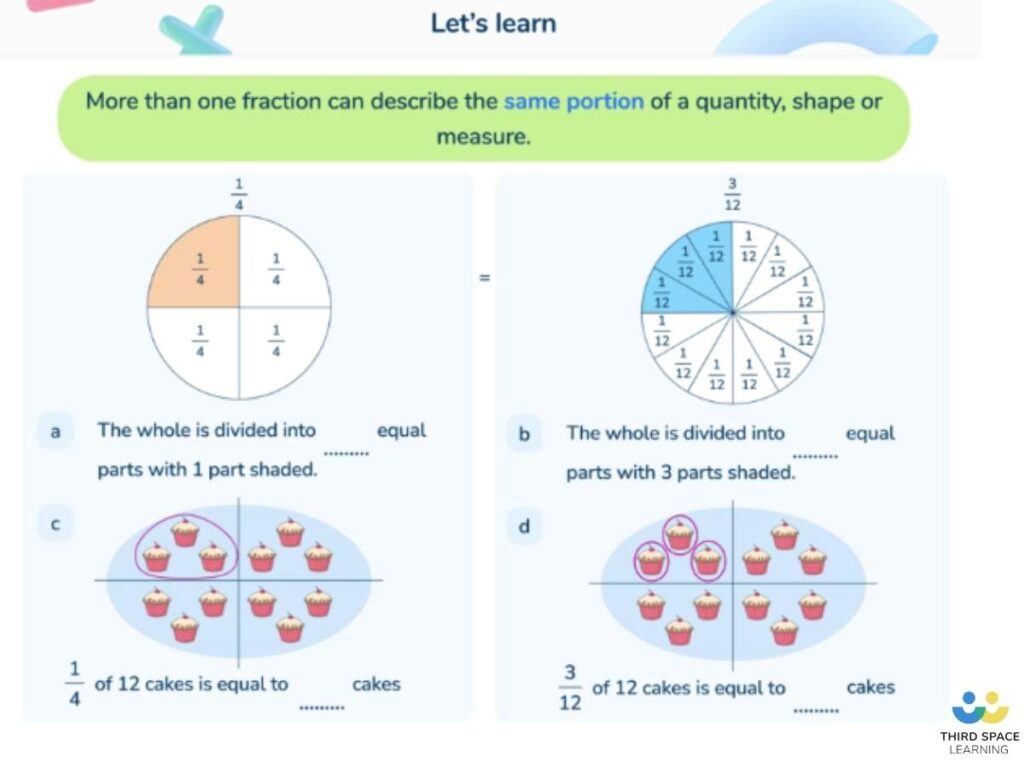
Fraction of an amount or set of objects

Find ⅗ of 20.

1. The denominator shows how many equal parts the whole has been split into (in this case, 5) so divide the whole amount by the denominator (in this case, 20 ÷ 5 = 4)
2. The numerator shows how many of those parts we need to find (in this case, 3) so multiply each part by the numerator (in this case, 4 x 3 = 12)

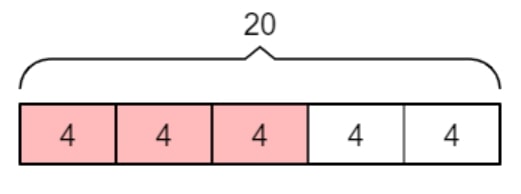
Addition or subtraction of non-unit fractions

¾ + ⅔     or     ¾ – ⅔ 

1. In order to add or subtract fractions with different denominators, first find the lowest common multiple of both denominators in order to achieve a common denominator (in this case, 12 can be used as a common denominator)
2. Use the common denominator to find equivalent fractions for each fraction (in this case, ¾ = 9⁄12 and ⅔ = 8⁄12, as shown below)

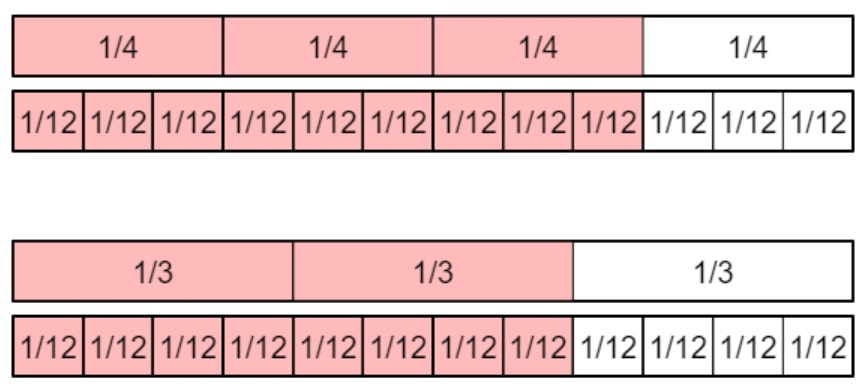
3. Once the denominators are the same, the numerators can be added or subtracted as appropriate (in this case, ¾ + ⅔ = 9⁄12 + 8⁄12 = 17⁄12 or 1 and 5⁄12; or ¾ – ⅔ = 9⁄12 – 8⁄12 = 1⁄12)

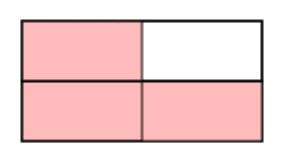
Shading fractions of various shapes

Shade ¾ of each shape.

For each shape, count how many equal parts the whole has been split into, then find the fraction (in this case, ¾) of that amount and shade it. 

This shape has been split into 4 equal parts; ¾ of 4 is 3, so any 3 parts can be shaded.

This shape has been split into 8 equal parts; ¾ of 8 is 6, so any 6 parts can be shaded.

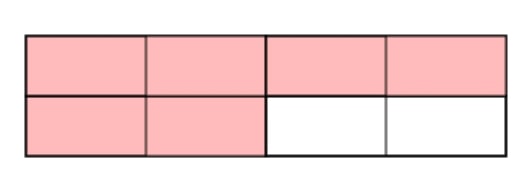
This shape has been split into 12 equal parts; ¾ of 12 is 9, so any 9 parts can be shaded.

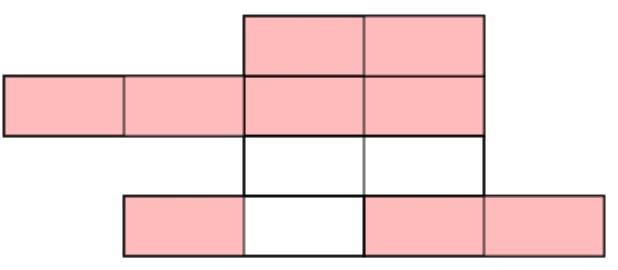
5 non-unit fraction practice questions and answers

1. What is 5⁄7 of 35?
   Answer: 25
2. ⅔ + ⅖ =
   Answer: 10⁄15 + 6⁄15 = 16⁄15 or 1 and 1⁄15
3. Shade ⅖ of this shape:

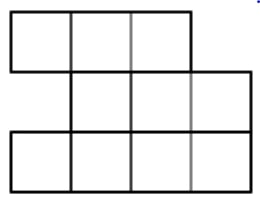
Answer: any 4 parts shaded, e.g.

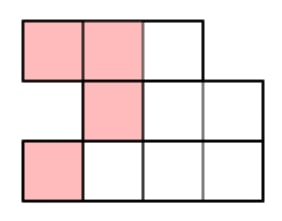
4.Continue the sequence: 2⁄3, 4⁄3, ___, ___, ___

Answer: 6⁄3 or 2, 8⁄3 or 2⅔, 10⁄3 or 3⅓ 

5. Use a fraction to complete this number sentence: 12 is ___ of 16

Answer: ¾ 

FAQs

For more definitions and explanations of math terms, refer to our Math Dictionary For Kids.

Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.

Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.

Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring

Why not learn more about how it works?

The content in this article was originally written by primary school teacher Sophie Bartlett and has since been revised and adapted for US schools by elementary math teacher Christi Kulesza.