What Is An Improper Fraction: Explained for Elementary School

Improper fractions and mixed numbers (a whole number with a fractional part) are introduced once children are secure in their understanding of proper fractions.

What is an improper fraction?

There are two main types of fractions: proper fractions, see fractions for kids (which include unit fractions and non-unit fractions) and improper fractions.

An improper fraction is a number greater than one whole. The numerator of the fraction (top number) is, therefore, greater than the denominator of the fraction (bottom number).

Examples of improper fractions

\frac {4}{3} , five halves, and \frac {927}{4} are all examples of improper fractions. Some improper fractions are actually equivalent to a whole number, such as 4⁄2 (four halves is the same as two wholes), but it can still be represented as an improper fraction. All whole numbers above 1 can be represented as improper fractions (e.g. 2 is the same as \frac {4}{2} , which is an equivalent fraction to \frac {6} {3} and \frac {16}{9} ,10 is the same as \frac {70}{7} , \frac {120}{12} , or \frac {530}{53} ,).

When do children learn about improper fractions in elementary school?

Children first encounter improper fractions in upper elementary school. In 3rd grade, students are introduced to the use of improper fractions to represent whole numbers (e.g. \frac {3}{1} = 3 wholes, \frac {17}{1} = 17 wholes, etc.). In 4th grade, students are expected to use mixed numbers when adding and subtracting mixed numbers with like denominators. They may need to convert the mixed number into an equivalent fraction.

While they are not explicitly referred to again in the standards, a solid understanding of improper fractions is beneficial when attempting more complex math in 5th grade and above.

Depending on the state and/or district curriculum a school follows, when these concepts are introduced may be different. 

How do improper fractions relate to other areas of math?

Besides coming alongside mixed numbers (also known as mixed fractions), or perhaps when identifying decimal equivalents, children are unlikely to come across improper fractions in any other areas of math. Some improper fractions may require simplifying to the lowest term, e.g. \frac{10}{4} = \frac{5}{2}

Improper fractions in real life

Mixed numbers are encountered more often in real-life contexts and can have everyday use, more so than improper fractions. However, sometimes it may be useful to think of ideas in terms of improper fractions first. For example, if you’re holding a party for 13 people, and each person would eat half a pizza, you would need 13 equal pieces (or \frac {13}{2} ) of a pizza – which is in its simplest form, 6\frac {1}{2} (the number of whole pizzas plus the fractional part).

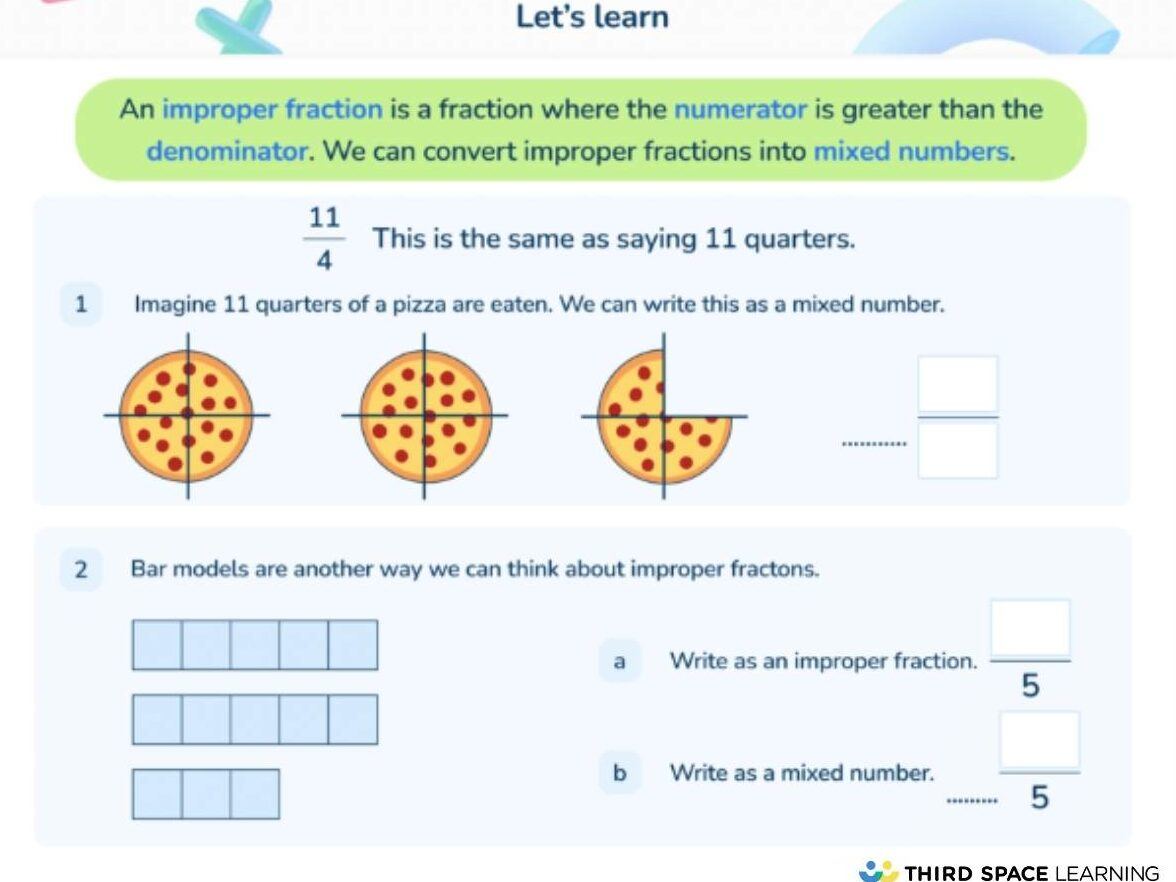
Worked examples for improper fractions

To convert an improper fraction to a mixed number, divide the numerator (in a division, this is also known as the dividend) by the denominator (also known as the divisor). The answer to this (also known as the quotient) becomes the whole number; the remainder (if there is one) becomes the numerator; the denominator (which was the divisor) remains the same.

For example, to convert \frac {23}{5} to a mixed number, step-by-step:

1. Divide 23 by 5.
2. 5 fits into 23 4 whole times, so the whole number is 4.
3. There is a remainder of 3, so the new numerator is 3 in the fraction part of the mixed number (the denominator remains the same as the original improper fraction). The answer is therefore 4\frac {3}{5} . 

This can be much more clearly visualized with a diagram such as a bar model:

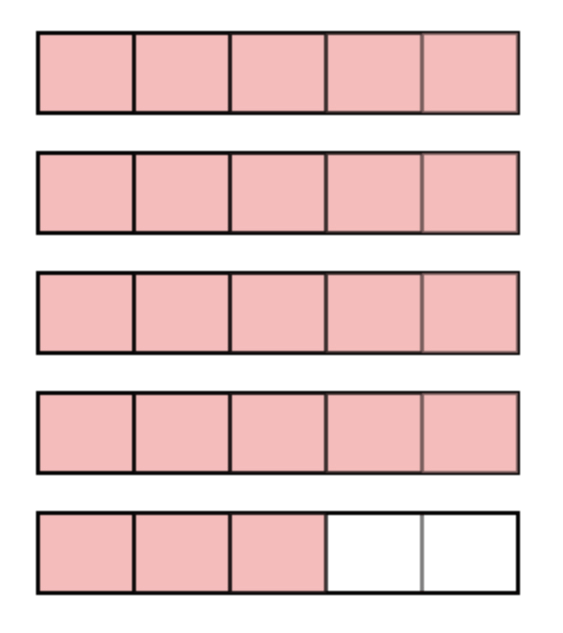
As shown above, twenty-three fifths can also be written as four wholes and three-fifths.

To convert a mixed number to an improper fraction, multiply the whole number by the denominator and add the numerator. The answer to this becomes the new numerator; the denominator remains the same. 

For example, to convert 2\frac {2}{3} to an improper fraction step-by-step:

1. 2 (whole number) x 3 (denominator) = 6
2. 6 + 2 (numerator) = 8 (the new numerator). The answer is therefore \frac {8}{3} .

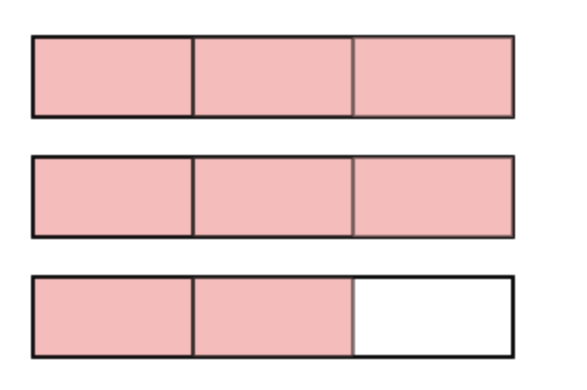
As shown above, two wholes and two-thirds can also be written as eight-thirds. 

As previously mentioned, converting to improper fractions may be useful when adding, subtracting and multiplying mixed numbers.

5 Improper fractions practice questions and answers

1. Which improper fraction is equivalent to 6\frac {7}{8} ?
   \frac {67}{8}     \frac {48}{8}     \frac {62}{8}     \frac {55}{8}     \frac {76}{8}
   Answer: \frac {55}{8}
2. Convert \frac {17}{3} to a mixed number.
   Answer: 5\frac {2}{3}
3. Convert 2 and \frac {5}{9} to an improper fraction.
   Answer: \frac {23}{9}
4. Which is the odd one out?
   2\frac {3}{4}     \frac {23}{4}     \frac {11}{4}     1 + \frac {7}{4}     3 - \frac {1}{4}
   Answer: \frac {23}{4} because the rest are all equivalent to 2\frac {3}{4}
5. Which mixed number is equivalent to \frac {37}{6} ?
   3 and \frac {6}{7} 6\frac {1}{6}     6 and \frac {6}{7}     \frac {55}{8}     7 and \frac {3}{6}
6. Answer: 6\frac {1}{6}

For more explanations of elementary math topics, take a look at Third Space Learning’s Math Dictionary.

Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.

Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.

Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring

Why not learn more about how it works?

The content in this article was originally written by primary school teacher Sophie Bartlett and has since been revised and adapted for US schools by elementary math teacher Christi Kulesza.