Teaching Division: A Guide For Elementary School Teachers
Division in elementary school forms the last part of the ‘Four Operations’ – the four core mathematical concepts all students should know. This blog will help you ensure all your students can approach division with the confidence they need to succeed.
Teaching Long Division Worksheets - Grade 3 to 5
Download this free pack of division worksheets, perfect for teaching division in your grade 3, 4 and 5 math classroom.
Download Free Now!Division is a skill which is built on each year in elementary school. By the end of 3rd grade, students working on grade level will be able to ‘know from memory all products of two one-digit numbers’.
For teachers in 4th grade, it is always a good idea to ensure that the students know this very well. By that, I do not simply mean that they can parrot the multiplication facts and their inverse at you, but that they truly understand how to represent these facts both with concrete representations, verbal explanations and through other pictorial methods.
Students who are not able to do this, yet who are able to verbally tell you the division facts, have a very shallow understanding of division and in order for them to progress onto more difficult problem solving activities, deepening their conceptual understanding of division is a must at 4th grade.
The Common Core State Standards places division within Numbers and Operations in Base 10 for grades 3-5 and places it within a section called ‘The Number System’ in 6th grade. The parts taken from the CCSS relate only to those that specifically mention division. The other elements of those sections can be found in the blog on multiplication or addition and subtraction, where appropriate.
Take a look at our guide to division methods and our collection of division worksheets for elementary school.
What is division?
Division is one of the Four Operations – the four core mathematical concepts students should know – alongside addition, subtraction and multiplication.
Where multiplication is combining one number multiple times, division is the opposite: working out how many times one number is contained within another. For example, dividing 10 by 2 is asking how many times 2 is contained within 10.
In a division, the first number (the amount being divided) is called the dividend; the second number (whatever the dividend is being divided by), is called the divisor; the answer is called the quotient. In the example used above, the dividend is 10, the divisor is 2 and the quotient is 5.

from Third Space Learning’s online math interventions.
Teaching division – Sharing, grouping and scaling
Division is the inverse of multiplication. As with the multiplication blog, the teaching of division contains three underlying structures, which, when coupled with division facts and conceptual understanding, will give students the best opportunity to be successful when solving problems related to division.
The three structures are sharing, grouping and scaling. While there is not enough time to explore these in depth, what follows will be just a short introduction to them.
Sharing and grouping
Sharing and grouping are the inverse of multiplication as repeated addition. Sharing is a structural concept that is introduced in lower grades in elementary school where, as the name suggests, an amount is shared into equal groups.
For example, 12 apples are shared amongst 3 students. How many apples does each student get?
Here we know the whole amount or dividend (12 apples) and crucially, we know how the amount we are going to share into (3 – the divisor).
Depending on where students are on their mathematical journey, they may repeatedly subtract by some number (1, 2, 3 or 4) from the amount into three piles which represent the three students.
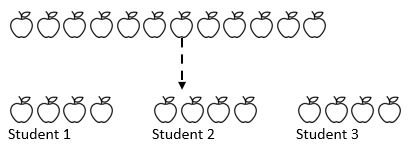
As we can see from the above, the whole amount has been shared into three equal groups.
Grouping is similar to sharing but what we know is slightly different when compared to sharing. In the sharing structure, we know the amount of groups that the sharing will take place. In the grouping structure, we know the amount in each group but not the number of actual groups that there are.
For example, 12 apples are shared in groups of 4. How many groups will there be? While this question is very similar to the one above, it now takes on the grouping structure as we know how many will go into each group but no longer know how many groups there will now be.
As we know that there are 4 in each group, we can group 4 apples until we have covered all 12 to see that there are 3 groups.
Scaling
The final structure of division is scaling. While in multiplication we were scaling up a value, the division structure scales down. For example, Shannen has 6 pens and Jen has 3 times as fewer. How many pens does Jen have?
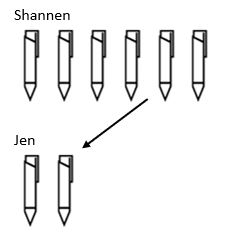
Here, we can see that to find the total amount of pens that Jen has, we had to take the amount that Shannen had and decrease it by a scale factor of 3 so that Jen ends up with 2 pens.
From experience, this is the hardest division structure for students to grasp and understand and is one that needs to be revisited in conjunction with scaling as multiplication as this is a crucial skill when converting measurements and currencies from a larger amount to a smaller amount, e.g. kilometers to miles.
Division 3rd grade
In the Common Core State Standards for math, division is taught in the domain “Operations and Algebraic Thinking”. The standards covered in Operations and Algebraic Thinking are as follows:
- interpret whole-number quotients of whole numbers, e.g., interpret 56 ÷ 8 as the number of objects in each share when 56 objects are partitioned equally into 8 shares, or as a number of shares when 56 objects are partitioned into equal shares of 8 objects each.
- Use multiplication and division within 100 to solve word problems in situations involving equal groups, arrays, and measurement quantities, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem.
- Determine the unknown whole number in a multiplication or division equation relating three whole numbers.
- Apply properties of operations as strategies to multiply and divide.
- Understand division as an unknown-factor problem.
- Fluently multiply and divide within 100, using strategies such as the relationship between multiplication and division or properties of operations.
- Know from memory all products of two one-digit numbers.
- Solve two-step word problems using the four operations.
Division: Lesson ideas 3rd grade
This will not cover a lesson, but provide a guide as to how division can be taught with some conceptual understanding at this stage. A prerequisite for this would be the teaching of related multiplication facts and times tables first before teaching any related division.
When thinking about structure, it is best at this part of students’ learning journey to stick with grouping and sharing. For the following examples, we will look at developing students’ understanding of dividing by 4. It will follow the Concrete-Representational-Abstract approach.
It is often students’ understanding of numbers that can limit their progress in division. Particularly when it comes to grouping and sharing when they only take one away continuously from the whole.
From the outset of teaching division, teachers should lean on what students already know about even numbers and other number facts to progress students onto counting in whatever number may be appropriate.
Counters can be used to demonstrate related division facts as students will have used these when building their conceptual understanding of multiplication. Questions such as, ‘How many groups of 4 are there?’ and ‘How many are there in each group?’ should be asked and the answers should relate to how this shows division.
Teacher: How many counters are there?
Child: Four.
Teacher: Good. This is a group of four. How many groups of four are there?
Child: One.
Teacher: Excellent. We have four counters in one group. We have grouped four counters into one group. What have we done?
Child: Grouped four counters into one group.
Teacher: Brilliant. When we group four counters into one group, we have done the mathematical calculation of four divided by one. What calculation did we do?
Child: Four divided by one.
Teacher: And when we solve four divided by one, the answer is four because we have made one group that has four items in it. Four divided by one is four. What is four divided by one?
Child: Four divided by one is four.
Teacher: Excellent.
You can see how that would be repeated for the following:
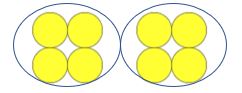
Teacher: How many counters are there?
Child: Eight.
Teacher: Good, this is a group of four. How many groups of four are there?
Child: Two.
Teacher: Excellent. We have four counters in one group. We have grouped four counters into two groups. What have we done?
Child: Grouped four counters into two groups.
Teacher: Excellent. When we group four counters into two groups, we have done the mathematical calculation of eight divided by two. What calculation did we do?
Child: Eight divided by two.
Teacher: And when we solve eight divided by two, the answer is four because we have made two groups that have four items in it. Eight divided by two is four. What is eight divided by two?
Child: Eight divided by two is four.
Teacher: Excellent.
When students are beginning to get confident with this, we can move on to other models such as Cuisenaire rods.

Here, the whole amount is represented in the top train and the purple rod (which, in this case, represents 4 and if you have read other blogs in this series, hopefully you will know how much of an advocate I am for their use in the classroom and so students will be aware of its value by then) is used to show the number of times groups of 4 can go into the total amount.
Students can then move on to drawing out scenarios based on division calculations read by the teacher. For example, there are 24 buttons and they need to be grouped into 4. How many groups are there? Students could draw those buttons and group them into 4, etc.
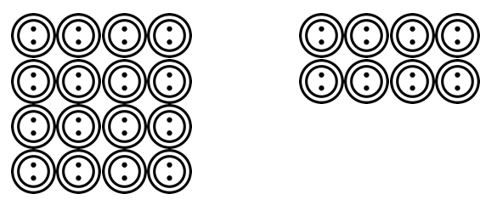
Once students have gotten used to being able to visualize these grouping or sharing division scenarios in a range of contexts, then they can move on to more abstract representations using mathematical symbols.
Division: Word problems 3rd grade
Word problems in 3rd grade will commonly use the grouping or sharing structure.
There are 40 cakes and 10 students. How many cakes would each student get?
As we know how many groups there are (10), we need to work out the amount per group so this is a sharing structure. Without a strong knowledge of the 4 times table, students will struggle with the process of dividing as they will need to use this knowledge to get the answer 4.
Division: Reasoning and problem solving 3rd grade
For reasoning and problem solving, a good activity I find is to match a word problem to a calculation. For example:
Match the word problems that are solved by knowing 20 divided by 4.
- There are 20 pencils and they are going to be placed into packs of 5. How many in each pack?
- There were 20 pencils and then a student brought in 4 more. How many pencils are there now?
- There are 20 pencils and they are going to be placed into packs of 4. How many in each pack?
- There were 20 pencils and then 4 went missing. How many pencils are there now?
Getting students to write down their explanations for each question is useful as it allows them to see their thinking. The questions have been selected carefully so that the numbers in each question relate to the numbers on the question so students are relying on their mathematical skills to deduce the correct answer.
Division 4th grade
In the Common Core State Standards for math, division is taught in the domains “Operations and Algebraic Thinking” and “Numbers and Operations in Base 10”. The standards covered in Operations and Algebraic Thinking are as follows:
- Multiply or divide to solve word problems involving multiplicative comparison, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem, distinguishing multiplicative comparison from additive comparison.
- Solve multistep word problems posed with whole numbers and having whole-number answers using the four operations, including problems in which remainders must be interpreted. Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation strategies including rounding.
Number and Operations in Base 10:
- Find whole-number quotients and remainders with up to four-digit dividends and one-digit divisors, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.
Division: Lesson ideas 4th grade
For this lesson, I will look at how you can begin to teach division using the area model with manipulatives alongside it to divide increasingly larger numbers.
Say we are going to teach students division for the question 168 divided by 8.
We would normally write this in what is commonly referred to as the ‘dog house’. But what is interesting is that different places in the world would write it differently.
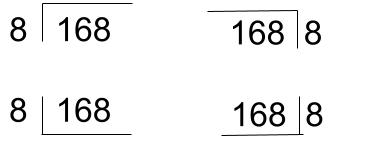
The reason for this is quite simple. What the ‘dog house’ actually represents is a shortened way to represent a rectangle.
When we teach formal division, what we are effectively saying is that you need to imagine a rectangle where the width is 8. The total area of the rectangle is 168 and we are attempting to find the missing length across the top. So how do we show this using manipulatives? Base 10 blocks are a useful tool for this.
We know the total amount is 168. So we need to gather 168 worth of base 10 blocks using the smallest amounts of blocks possible. This is shown below.
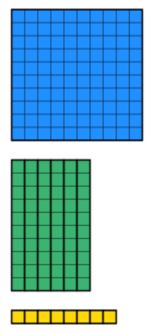
Looking back at the question, we know that the width is 8. That means we now need to manipulate the blocks so that we get a width of 8. Note that the rectangle needs to be solid and can have no missing parts. For example, the below would not be allowed despite there being 8 units going down the width.
Instead, students can decompose the 100s block into ten – 10s blocks. Notice how you can now place 8 in each column and it is a solid object.
The final part the students must do is use the remaining blocks to create a solid rectangle while keeping the width 8. This could take some time but with practice, students do get quicker. After some time, students will produce this:
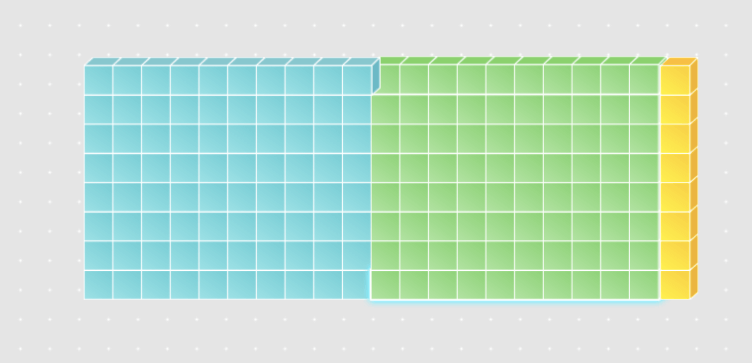
We can see that all 168 worth of blocks have been used up and that the width is still 8. To find the answer, students are required to count the length which in this case is 21. I have superimposed both methods below so you can see how they complement each other.
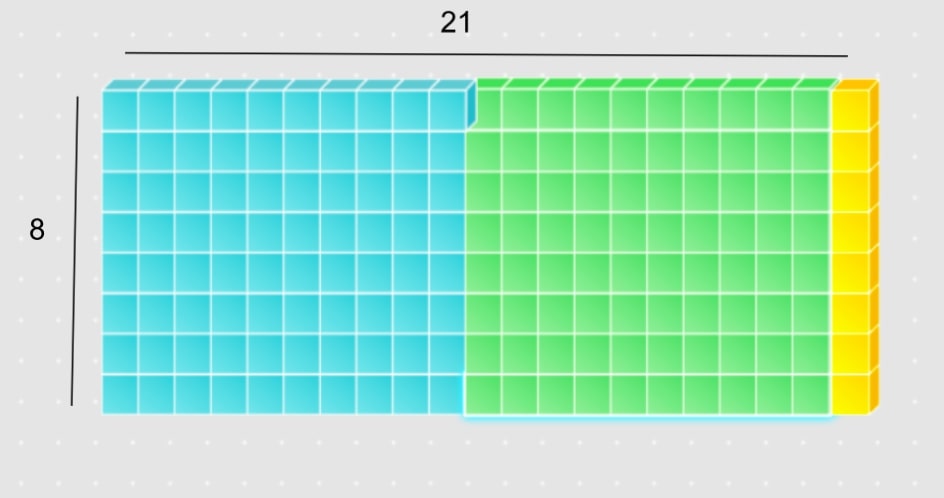
This is a useful strategy to teach students in 4th grade as there are massive repercussions in other areas of the curriculum that are already illuminated to students.
Though they may not recognise it yet, by teaching division like this they have already been introduced to perimeter and area – think how much teaching time can be saved when this connection is made. Not only that, but in secondary school, this approach transfers to algebraic thinking.
Division: Word problems 4th grade
Students would be expected to draw on their knowledge of place value to solve division-based problems and so an appropriate word problem would be:
An orchard grows 4,800 apples in a season. They are placed in packs of 4 before going to the market. How many packs are there?
Here, students should use the fact that 4 x 12 = 48 and as 4,800 is a hundred times more than 48, 12 must also by multiplied by 100 to get 1,200
Division: Reasoning and problem solving 4th grade
Is it always, sometimes or never true that the sum of three even numbers is divisible by 4?
This question gives students ample opportunity to experiment within the parameters of the question. Students who need more support can look at single digit even numbers and students could go up to whatever they feel comfortable with.
With open questions such as this, it is good to provide a minimum requirement for how many attempts students should make, otherwise they will often choose to do the bare minimum.
A quick ‘trick’ to know if a number is divisible by 4 is to look at the last 2 digits of the number and see if those are divisible by 4.
For example, if a child found the sum of 34, 36 and 38 and got 108, as a teacher I know that this number is divisible by 4 as the final two digits (08) make 8 and are divisible by 4. If a child chose 34, 36 and 48 to get 118, I know that this is not divisible by 4 as 18 – the final two digits of 118 – are not divisible by 4.
Division 5th grade
In the Common Core State Standards for math, division is taught in the domains “Numbers and Operations in Base 10” and “Numbers and Operations – Fractions”. The standards covered in Numbers and Operations in Base 10 are as follows:
- Find whole-number quotients of whole numbers with up to four-digit dividends and two-digit divisors, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.
- Add, subtract, multiply, and divide decimals to hundredths, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method and explain the reasoning used.
Numbers and Operations – Fractions:
- Interpret a fraction as division of the numerator by the denominator (a/b = a ÷ b). Solve word problems involving division of whole numbers leading to answers in the form of fractions or mixed numbers, e.g., by using visual fraction models or equations to represent the problem.
- Apply and extend previous understandings of division to divide unit fractions by whole numbers and whole numbers by unit fractions.
- a. Interpret division of a unit fraction by a non-zero whole number, and compute such quotients. For example, create a story context for (1/3) ÷ 4, and use a visual fraction model to show the quotient. Use the relationship between multiplication and division to explain that (1/3) ÷ 4 = 1/12 because (1/12) × 4 = 1/3.
- b. Interpret division of a whole number by a unit fraction, and compute such quotients. For example, create a story context for 4 ÷ (1/5), and use a visual fraction model to show the quotient. Use the relationship between multiplication and division to explain that 4 ÷ (1/5) = 20 because 20 × (1/5) = 4.
- c. Solve real world problems involving division of unit fractions by non-zero whole numbers and division of whole numbers by unit fractions, e.g., by using visual fraction models and equations to represent the problem. For example, how much chocolate will each person get if 3 people share 1/2 lb of chocolate equally? How many 1/3-cup servings are in 2 cups of raisins?
Division: Lesson ideas 5th grade
Division in 5th grade progresses through the use of remainders in answers. For this activity, I will look at another use of manipulatives that teachers can use to teach 4 digit by 1 digit division.
If the question was 5,642 divided by 4, we could represent this using a place value chart and place value counters as we can see below.
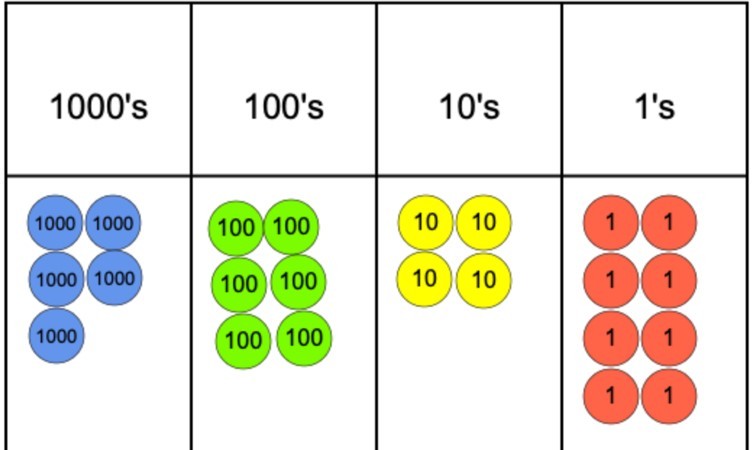
The next step would be to begin to group the counters into 4 as this is our divisor. However, as can be seen, we quickly come to a problem in the 1000’s column as we are able to group 4 of the counters but then we cannot group the remaining counter in a group of 4.
To combat this issue, the 1000 counter that has not been grouped can be exchanged for ten 100 counters. These can then be grouped into groups of 4 and this can happen without there being any 100s counters left over. From there, it is a simple case of then moving to the 10s and finally the 1s.
As there are nine 1s counters, we can group 8 of them into 2 groups of 4 and claim that there is one left over*. To find the answer, all that is required is to count the number of groups made in each place value and use these to write the digits to create the final answer. In this case, the answer would be 1,412 remainder 1.
*When you are looking at decimals, you can exchange the remaining 1s counter for ten 0.1 counters and carry on the division as described above.
Students being familiar with this model is useful as it can help to demystify division with decimals which students can struggle with.
This helps them see that it is a continuation of a process that they are already familiar with rather than something new.
Division: Word problems 5th grade
When dividing in 5th grade, students will come across scenarios where they will need to round their answer up in order for the answer to make sense in the context. An appropriate question that demonstrates this would be something like the following:
A school is planning a disco where they plan on offering 250ml of juice to each student. They can buy 2 liter bottles of juice. They are expecting 33 students to arrive so they know that they will give out 8.25 liters of juice. How many bottles of juice will they need to buy?
A common answer is that students will say 4 and a quarter. However, as you cannot buy a quarter of a bottle, in this instance, the correct answer would be 5 bottles of juice would be needed to ensure that all students could partake.
Division: Reasoning and problem solving 5th grade
Getting students to create their own problems using a range of provided context can be a really challenging activity that gets the students thinking mathematically about context and division.
Students can then swap these questions they have created with a partner and then go about solving them and checking with the original question creator if they have the correct answer.
Division 6th grade
In the Common Core State Standards for math, division is taught in the domain “The Number System.” The standards covered in The Number System are as follows
- Fluently divide multi-digit numbers using the standard algorithm.
- Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation.
- Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions, e.g., by using visual fraction models and equations to represent the problem
Division: Lesson Ideas 6th grade
Sophie Bartlett (@_MissieBee) has created an excellent blog on teaching long division, detailing how she would teach long division for a 6th grade class. As long division is the only new learning on division for 6th grade, this is an ideal way to introduce the procedure of long division.
Read more: Long Division Examples
Division: Word problems 6th grade
A typical division word problem that a 6th grade student would come across would be:
A school raised $3,146 from a bake sale. 104 parents attended the event. If all parents spent an equal amount of money, how much did each parent spend?
Here, students would be expected to use the long division method to solve this question to get the answer $30.25.
Division: Reasoning and problem solving 6th grade
With something procedural like long division, a good reasoning activity is to get students to find mistakes.
As we can see from the question below, the student has done all the hard work but a careless error in counting the groups of 59 means that the child believed 59 x 7 was 472 and not 59 x 8.
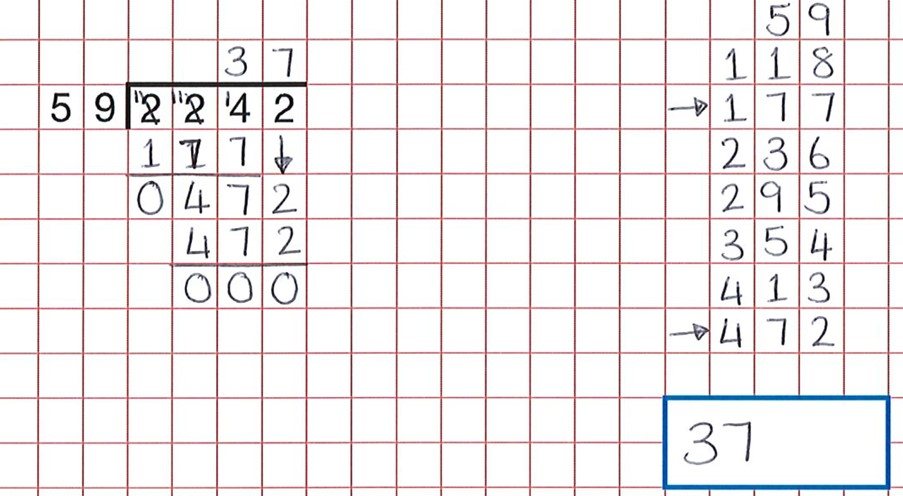
The correct answer would have been 38.
Division is a key math topic, not just at elementary school but in math as a whole. Hopefully this post has given you some good ideas to help your students approach it with confidence.
See also:
- Division Questions That Will Test Your Primary School Students
- Long Division Questions That Will Test All Students From Sixth Grade to Seniors
- Partitioning Explained For Teachers, Parents And Kids
- How To Teach Division: Math Bootcamp
Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.
Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.
Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring
Why not learn more about how it works?
The content in this article was originally written by primary school lead teacher Neil Almond and has since been revised and adapted for US schools by elementary math teacher Christi Kulesza.





