What Is Division With Remainders? Explained For Elementary School and Middle School

Division with remainders, and division more generally, is a key skill taught in upper elementary school math through the first year of middle school. Students in upper elementary will be introduced to division calculations with remainders – where there is a certain amount left over.

In this article, we will explain division with remainders and provide worked examples, including word problems, to support your teaching of division with remainders to your elementary schoolers.

The four operations (addition, subtraction, multiplication and division) are a key part of the math curriculum throughout elementary school. Teaching of division starts in 3rd grade, where children are only taught division where the answers are exact, with no remainder. Starting in 4th grade, students will need to be comfortable working with division problems with remainders.

What is division with remainders?

Division with remainders is a division calculation without an exact answer – the answer will have a particular amount left over.

• The first number (the amount being divided) is called the dividend;
• The second number (whatever the dividend is being divided by), is called the divisor;
• The answer is called the quotient.

In a division calculation with remainders, we therefore say the quotient will have a particular amount left over. This remainder can be expressed as a standard remainder (written as ‘r’ and then the remainder) or a fraction (the remainder becomes the numerator and the divisor becomes the denominator).

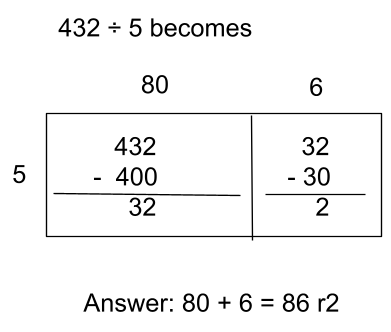
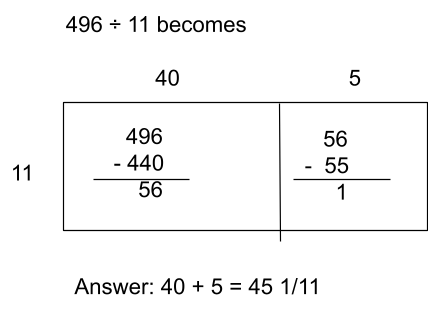
For example, when dividing using rectangular arrays or area models, 432 ÷ 5 = 86 r2 (standard remainder) and 496 ÷ 11 = 45 \frac{1}{11} (fraction remainder).

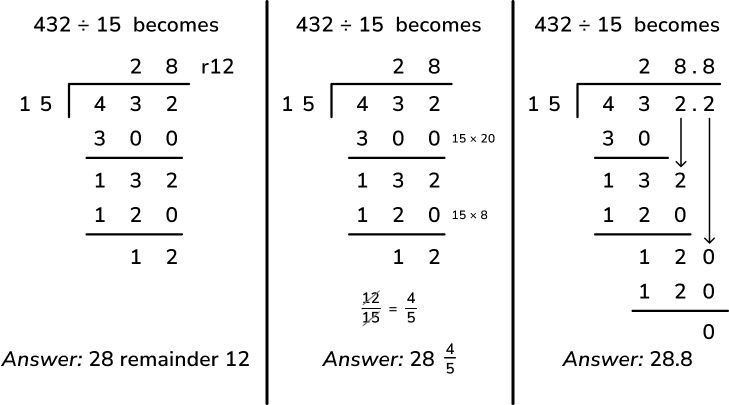
Starting in 6th grade, students will begin division with long division, or the standard algorithm. The problem 432 ÷ 15 can be expressed as 28 r12, 28  \frac{4}{5}  or 28.8, as in these examples below.

See also: What Is Division?

How to work out division with remainders

In a division with remainders, the remainder will always be smaller than the divisor. If it is bigger, an error has been made as this means another ‘group’ could be made out of that remainder.

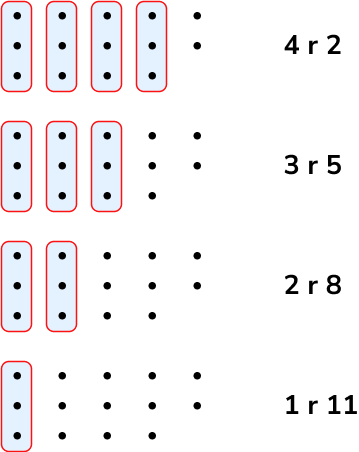
For example, take 14 ÷ 3. There are 4 groups of 3 in 14 with 2 left over – this is expressed as 4 r2. Technically, as in the second example below, this could also be written as 3 r5, however we can make another group of the divisor (3) out of the remainder (5), which would then turn it into 4 r2 as the original answer.

Likewise, this could also technically be written as 2 r8 (although we could make 2 more groups of the divisor from the remainder here) or 1 r11 (we could make 3 more groups of the divisor from this remainder), but the original answer of 4 r2 is the mathematically correct one.

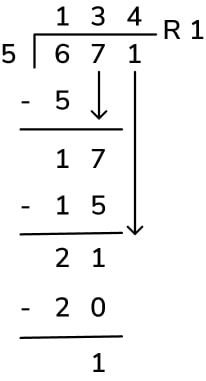
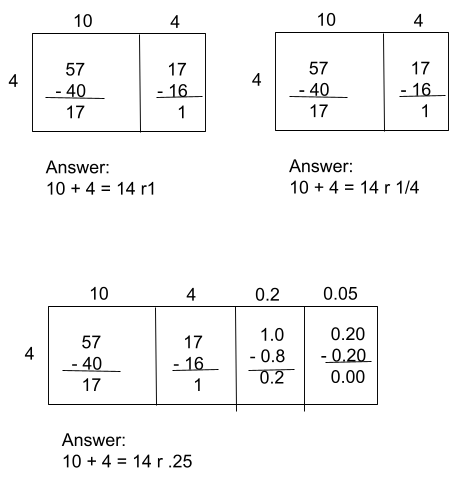
This concept is the same with long division and all division methods. Remember that the remainder can be expressed in one of three ways.

• As a remainder (e.g. r1 in the example below)

• As a fraction (e.g.  \frac{1}{5} in the example below – the remainder of 1 becomes the numerator of the fraction and the divisor, 5, becomes the denominator).

• As a decimal

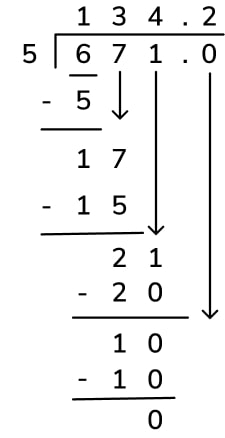
The method is the same as above but once the division of the ones digit has been completed, add a decimal point and a zero to the end of the dividend to essentially ‘continue’ the division (continue to ensure the place value digits are aligned correctly).

In this case, after calculating that 21 ones divided by 5 is 4 ones with 1 remaining, the 1 remaining ones can be seen as 10 tenths instead. We can then divide 10 tenths by 5, which is 2 tenths, hence the quotient being 134.2.

This is the same as 134 r1 or 134 \frac{1}{5} as, when dividing by 5, a remainder of 1 is the same as \frac{1}{5}, which is equivalent to 2 tenths.

If the decimal remainder is longer than one decimal place, continue to add 0s to the dividend until the division is complete or if the decimals continue for a long time, as in the example below of 425 ÷ 7, just round up to the required degree of accuracy – in this case, 60.7 to 1 decimal place (or 60.7143 to 3 decimal places).

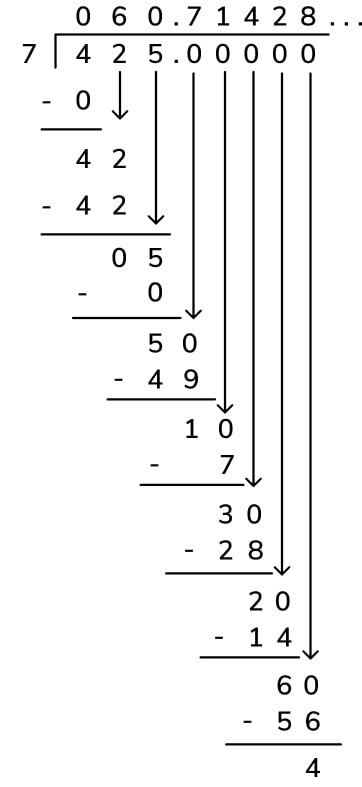
Division problems with a remainder longer than 2 decimal places are unlikely to be asked of children in elementary school.

However, it is useful to know how to interpret these answers – especially how to round decimal places – as divisions completed on calculators might give answers with many decimal places and children will need to understand what this means.

This process is the same for when you do the long division method. For example, 9,139 ÷ 21 can be expressed as 435 r4, 435 \frac{4}{21} or 435.19 (rounded to 2 decimal places).

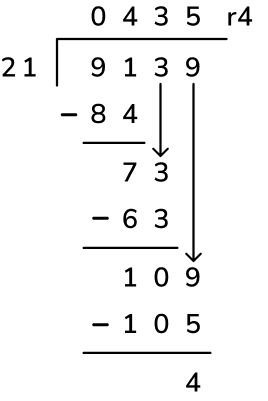
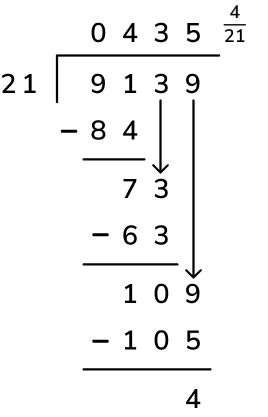
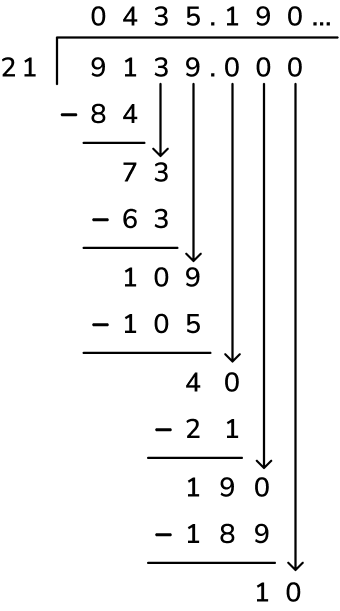
Division with remainders examples

See examples below of short area models with remainders expressed in all three ways.

The 3rd example of the four-digit division below is an example of a recurring decimal remainder – in this case, the digit 3 would continue on forever, so it is better to express this remainder as a fraction ( \frac{1}{3} in this case).

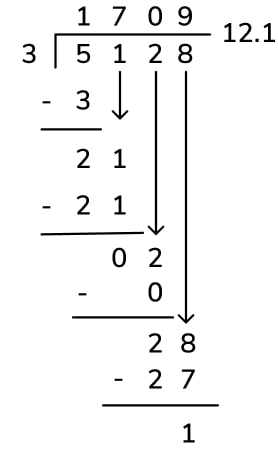
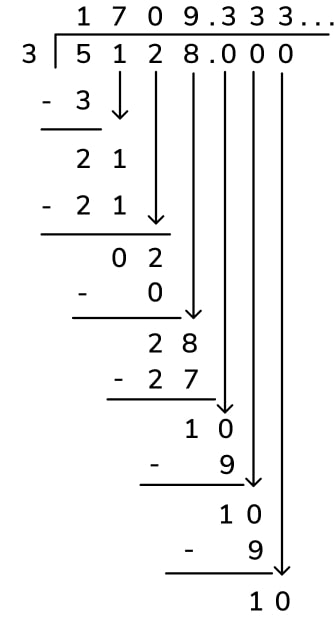
The remainder of these long division problems can also be expressed in three different ways (the method is the same even with large numbers as divisors).

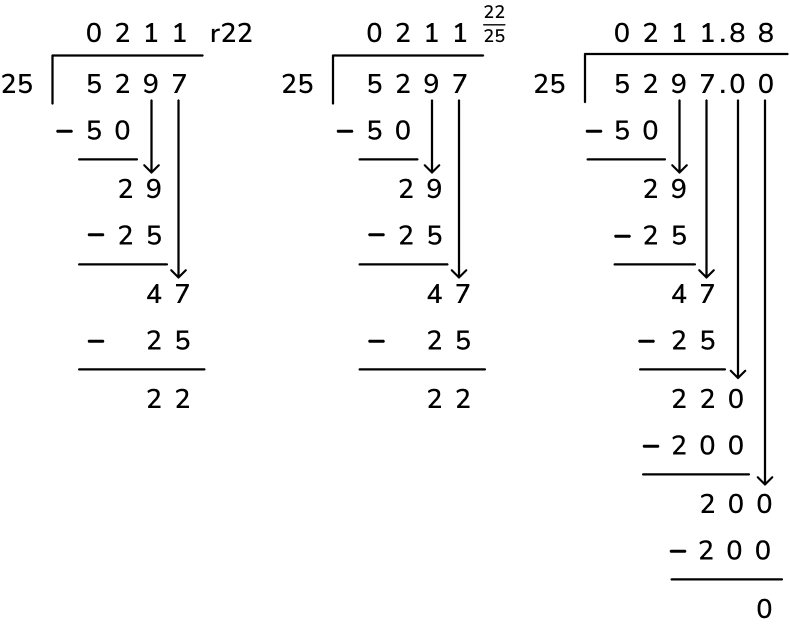
When do children learn about division with remainders in school?

The Common Core Math curriculum states that 4th graders should be taught to divide numbers up to 4 digits by a one-digit number, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.

5th graders should be taught to find whole-number quotients of whole numbers with up to four-digit dividends and two-digit divisors, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division.

Students should be able to illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.

5th graders could also connect equivalent fractions > 1 that simplify to integers with division and other fractions > 1 to division with remainders, using the number line and other models, and hence move from these to improper and mixed fractions.

6th graders are introduced to division with the standard algorithm, or long division. By the end of 6th grade, students will fluently divide multi-digit numbers using the standard algorithm.

Learn more about how to teach division in our article.

How does division with remainders relate to other areas of math?

In 5th grade, as children are required to calculate decimal fraction equivalents for a simple fraction, they may need to complete a division with a decimal remainder.

For example, to work out the decimal equivalent of \frac{5}{8} children would need to divide 5 by 8, which can be made into 5.000 ÷ 8 in this case as the answer (0.625) has 3 decimal places.

How does division with remainders link to real life?

Whenever something needs to be shared between two or more groups, division is required, with or without remainders. The suitable ‘type’ of remainder depends on the context of the problem.

‘Standard’ or fraction remainders would be appropriate in contexts where an exact answer is not necessarily required. For example, 267 people need transportation on a bus trip and buses each hold 42 people. 267 ÷ 42 = 6 r15, or 6 \frac{15}{42} , or 6.36 (rounded to 2 decimal places).

We can’t have part of a bus, so we would need 7 buses here (rounding up to the nearest whole number). The decimal remainder would be trickier to interpret (what is 0.36 of a bus?) but the other remainders tell us that there would be 15 people left for the 7th bus while the others would be full.

Decimal remainders would be more appropriate in contexts such as money. For example, a $188 bill split between five people is 188 ÷ 5 which is 37 r3, or 37 \frac{3}{5} , or 37.6. The decimal remainder here lends itself to a monetary context – in this case, each person would owe $37.60.

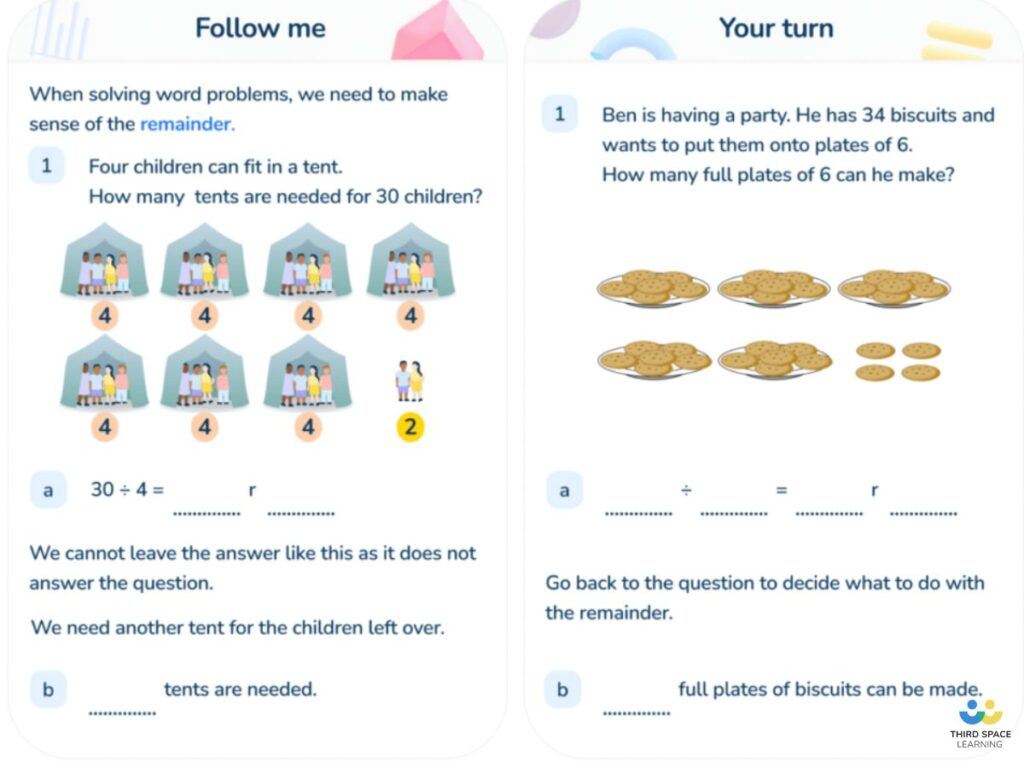
Dividing with remainders worked examples

1. 96 students and teachers go by minibus to a football tournament. How many 15-seater mini buses will be required?

96 ÷ 15 = 6 r6 (this could be done with a written division method but in this case it is easier to count in 15s to see how many fit into 96 – 15, 30, 45, 60, 75, 90 = 6 groups). There is a remainder of 6 which means 6 people are left without a coach, so 7 mini buses would be required.

2. Complete the number sentences:

a) 340 ÷ 7 = ___ remainder ___

b) ___ ÷ 3 = 295 remainder 2

a) Use an area model to get the answer 48 remainder 4

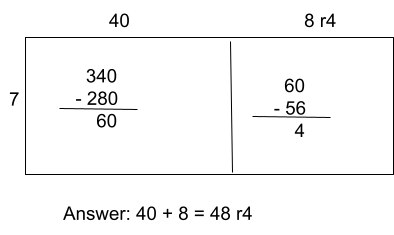
b) As the dividend here is missing, we need to use the inverse to work it out. Imagine the question was __ ÷ 2 = 3 remainder 1. We can work out the dividend by multiplying the divisor by the quotient and adding the remainder: 3 x 2 + 1 = 7, so 7 ÷ 2 = 3 remainder 1.

The same method applies here – multiply the divisor (3) by the quotient (295) and add the remainder (2) – this gives us 887, so the answer is 887 ÷ 3 = 295 remainder 2.

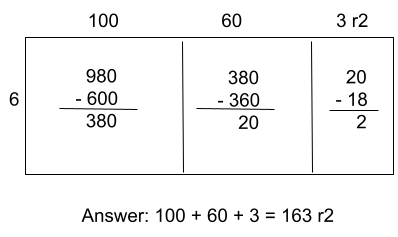
3. A grocer is packing eggs. Each box holds 6 eggs. The grocer has 980 eggs to pack. How many boxes can she fill and how many eggs will be left over?

Using an area model, we can work out that the grocer can fill 163 boxes and there will be 2 eggs left over.

Dividing with remainders practice questions

1. There are 275 children in Blockley School. They get into groups of eight. What is the largest number of groups of eight that they can make?
   Answer: 34 groups
   
2. Which two division expressions have an answer of 5 r2?
   a) 17 ÷ 5
   b) 17 ÷ 3
   c) 22 ÷ 4
   d) 22 ÷ 5
   Answers: b) and c)
   
3. Martha wants to buy a toy that costs $18.49. She saves $1.50 per week. How many weeks does she have to save before she can buy the book?
   Answer: 13 weeks
   
4. Write the missing number in each calculation:
   a) 25 ÷___ = 3r4
   b) 35 ÷ ___ = 4r3
   Answers: a) 7; b) 8
   
5. A bag has 90 marbles in it. 4 children take 20 marbles each. How many marbles are left in the bag?
   Answer: 10 marbles

Looking for more resources for teaching division? Why not check out our articles all about division questions and ourdivision worksheets.

Read more:

• How To Teach Division
• Partitioning Explained For Elementary School
• What We’ve Learnt From Teaching Our Long Division Lesson 2,968 Times
• 4th Grade Math Problems
• 7th Grade Math Problems

Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.

Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.

Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring

Why not learn more about how it works?

The content in this article was originally written by primary school teacher Sophie Bartlett and has since been revised and adapted for US schools by elementary math teacher Christi Kulesza.