What Is Division? Explained For Teachers, Parents and Kids
What is division? There are four basic operations in math: addition, subtraction, multiplication and division. Children will encounter all of these in elementary school. From experience, children tend to find division the trickiest to grasp.
What is division?
Division is a mathematical operation which involves the sharing of an amount into equal-sized groups. For example, “12 divided by 4” means “12 shared into 4 equal groups”, which would be 3.
In mathematics, this is written with the division symbol, called an obelus → ÷. Division can also be presented as a fraction: in this case, 12/4 (the division sign is represented as a forwards slash) or \frac{12}{4} (the division sign here is represented as a horizontal line). These are all equal to 3.
In a division, the first number (the amount being divided) is called the dividend; the second number (whatever the dividend is being divided by), is called the divisor; the answer is called the quotient. So, in the example above, 12 is the dividend, 4 is the divisor and 3 is the quotient.
Teaching Long Division Worksheets
Help your students with all aspects of long division with this ready-to-use long division worksheet. Includes 3 worksheets with questions and answers on division!
Download Free Now!
Remainders
Sometimes a number cannot be shared into equal groups with an integer (whole number) as an answer, so we are left with a remainder.
Take 13 ÷ 4 – we cannot split 13 equally into 4 groups (unless we venture into decimal numbers), so we would be left with 4 groups of 3 and 1 left over. In mathematics, this would be written as 3 remainder 1 (or 3 r1), so 13 ÷ 4 = 3 r1.
Learn more about division with remainders here.
Division and its inverse: multiplication
Division is often referred to as the opposite of multiplication. In the example 12 ÷ 4 = 3, we can use the inverse to see that 3 x 4 = 12. Likewise, where 12 ÷ 3 = 4, the inverse is that 4 x 3 = 12.
While “dividing by 4” is usually seen as “sharing into 4 equal groups”, it could also be seen as “how many equal shares of 4 can be made?”. Despite the similar wording, there is a distinct difference between the two.
See the first example below of 12 ÷ 4 – this shows 12 being shared into 4 equal groups (with 3 in each group). In the second example of 12 ÷ 4, it shows how many equal groups of 4 can be made – which is 3. Ultimately, the answers (quotients) are the same!
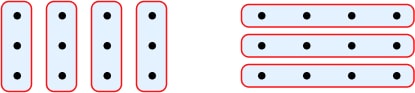
Division facts
If a number is divisible (which means it can be divided) by a one-digit number with no remainder (the quotients in these examples would be called factors), there is often a quick way to tell without having to actually work it out! A number is…
- …divisible by 2 if it is even (i.e. ends in one of the following digits: 0, 2, 4, 6 or 8)
e.g. 746 is divisible by 2 (can be divided by 2 without a remainder, or has 2 as a factor) - …divisible by 3 if the sum of the digits is a multiple of 3
e.g. 471 is divisible by 3 because 4 + 7 + 1 = 12 and 1 + 2 = 3, which is a multiple of 3 - …divisible by 4 if the last 2 digits make a multiple of 4
e.g. 7,324 is divisible by 4 because 24 is a multiple of 4 – this works because subtracting the last two digits leaves you with a multiple of 100, and every multiple of 100 is also a multiple of 4 - …divisible by 5 if the last digit is a 0 or 5
e.g. 285 is divisible by 5 - …divisible by 6 if the number is divisible by both 2 and 3 (see rules above)
e.g. 438 is divisible by 6 because it’s even and its digit sum is a multiple of 3 (4 + 3 + 8 = 15, 1 + 5 = 6) - …divisible by 8 if the last 3 digits make a multiple of 8 (so this will require a bit more working out!)
e.g. 42,976 is divisible by 8 because 976 is a multiple of 8 (978 ÷ 8 = 122) – this works because subtracting the last three digits leaves you with a multiple of 1,000, and every multiple of 1,000 is also a multiple of 8 - …divisible by 9 if the sum of the digits is a multiple of 9
e.g. 7,281 is divisible by 9 because 7 + 2 + 8 + 1 = 18 and 1 + 8 = 9 - …divisible by 10 if the last digit is a 0
e.g. 91,420 is divisible by 10
How to explain division
To introduce division, start with smaller numbers and the concept of sharing in equal groups, e.g. my friend and I have 6 sweets and we want to share them between us – how many do we each get? By taking one sweet, giving one to my friend, taking another, giving another to my friend, taking one more and giving the last one to my friend, we can easily see we’d have 3 each.
As well as the concept of sharing, we can talk about grouping when we discuss division. In the problem above, instead of thinking about sharing between 2 people, we would talk about groups of 2 – how many groups of 2 can be made? By pairing up the sweets, we can make 3 groups.
Grouping and sharing are two ways of discussing division (as also previously referred to for 12 ÷ 4).
However, there are other ways, such as repeated subtraction and using more formal methods (particularly useful as children move onto larger numbers) – see how to teach division for more support for whole classroom teaching and our division intervention blog to target individual students.
When do children learn about division in school?
Children learn the concept of division starting in the 1st grade, but the formal method of division isn’t introduced until 4th grade.
| Grade | Student Expectations |
| 1 | Partition circles and rectangles into two and four equal shares, describe the shares using the words halves, fourths, and quarters, and use the phrases half of, fourth of, and quarter of. Describe the whole as two of, or four of the shares. Understand for these examples that decomposing into more equal shares creates smaller shares. |
| 2 | Partition circles and rectangles into two, three, or four equal shares, describe the shares using the words halves, thirds, half of, a third of, etc., and describe the whole as two halves, three thirds, four fourths. Determine whether a group of objects (up to 20) has an odd or even number of members, e.g., by pairing objects or counting them by 2s; write an equation to express an even number as a sum of two equal addends. |
| 3 | Interpret whole-number quotients of whole numbers, e.g., interpret 56 ÷ 8 as the number of objects in each share when 56 objects are partitioned equally into 8 shares, or as a number of shares when 56 objects are partitioned into equal shares of 8 objects each. For example, describe a context in which a number of shares or a number of groups can be expressed as 56 ÷ 8. Fluently multiply and divide within 100, using strategies such as the relationship between multiplication and division (e.g., knowing that 8 × 5 = 40, one knows 40 ÷ 5 = 8) or properties of operations. By the end of Grade 3, know from memory all products of two one-digit numbers. |
| 4 | Find whole-number quotients and remainders with up to four-digit dividends and one-digit divisors, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models. Multiply or divide to solve word problems involving multiplicative comparison, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem, distinguishing multiplicative comparison from additive comparison. Solve multistep word problems posed with whole numbers and having whole-number answers using the four operations, including problems in which remainders must be interpreted. Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation strategies including rounding. |
| 5 | Find whole-number quotients of whole numbers with up to four-digit dividends and two-digit divisors, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models. Add, subtract, multiply, and divide decimals to hundredths, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method and explain the reasoning used. Solve real world problems involving multiplication of fractions and mixed numbers, e.g., by using visual fraction models or equations to represent the problem. Apply and extend previous understandings of division to divide unit fractions by whole numbers and whole numbers by unit fractions. |
| 6 | Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions, e.g., by using visual fraction models and equations to represent the problem. Fluently divide multi-digit numbers using the standard algorithm. Fluently add, subtract, multiply, and divide multi-digit decimals using the standard algorithm for each operation. |
How does division relate to other areas of math?
As mentioned frequently throughout the curriculum, children are required to know their times tables and related division facts before the end of 3rd grade. However, another key part of the math curriculum – introduced right from first grade – is fractions. A fraction is, essentially, a division.
Take one-half ( \frac{1}{2} ) for example: this literally means 1 ÷ 2; one shared into two equal groups is \frac{1}{2} (or 0.5). Here, the numerator (top number of the fraction) is the dividend; the denominator (bottom number of the fraction) is the divisor, and the fraction itself is the quotient!
As another example, look at three-eights \frac{3}{8} ): 3 ÷ 8, or three shared into eight equal groups, is \frac{3}{8} (or 0.375).
In order to understand fractions, children must fully understand the process of dividing – at first by 2 and 4 (as first graders are expected to find \frac{1}{2} s and \frac{1}{4} s of objects, shapes and quantities); then by 3 (2nd grade); then by any one-digit number (3rd grade).
How does division link to real life?
Division is required whenever something needs to be shared equally between two or more groups. This could be cost (e.g. a $174 bill between four people), distance (e.g. working out the halfway point between two destinations), weight (a 2lbs bag of apples shared three ways) or much more!
It is important to convey to students how division plays into everyday life. At Third Space Learning, we try to incorporate real world division problems into our one-to-one online math lessons. Personalized to each student’s unique needs, our online tutoring aims to fill gaps in math knowledge.
In addition to online tutoring, Third Space Learning offers an extensive collection of worksheets, learning and teaching resources to support students and teachers.
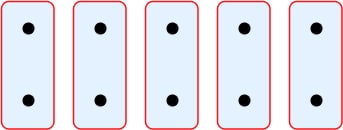
Division worked examples
- There are 10 sweets. Milly and her friend want to share them. How many do they each get?
The division here is 10 ÷ 2. Through the concept of sharing, the diagram below shows 10 sweets shared into 2 groups, resulting in 5 in each group.

Through the concept of grouping, the diagram below shows 10 sweets grouped in 2s, resulting in 5 groups.
- 65 children take part in a quiz. There are 5 children in each team. How many teams are there altogether?
We could either count up in 5s until we reach 65 (13 times), or use our knowledge that 10 lots of 5 is 50, and we’d need 3 more 5s to make 65, so that is 13 lots of 5. Either way, we’d reach the answer of 13 teams.
- Sam is making booklets. Each booklet must have 34 sheets of paper. He has 2 packets of paper. There are 500 sheets of paper in each packet. How many complete booklets can Sam make from 2 packets of paper?
2 packets x 500 sheets = 1,000 sheets of paper. Using long division, we can calculate that 1,000 ÷ 34 = 29 r 14. Sam can’t make a complete booklet out of 14 sheets, which means that he can only make 29 complete booklets.
Division practice questions
- Kim has $0.15. She wants to share it equally between her and her two friends. How much would they each get?
Answer: $0.05 each - 36 ÷ 4.
Answer: 9 - A length of rope measures 224cm. It needs to be cut into 4 equal sections. How long is each section?
Answer: 56cm - 2,464 ÷ 7.
Answer: 352 - Eggs are put in trays of 12. The trays are packed in boxes. Each box contains 180 eggs. How many trays are in each box?
Answer: 15 trays
There are four properties within division: the dividend, divisor, quotient and remainder.
Division is sharing an amount equally.
Division is used to share an amount equally or to split an amount into equal groups.
Divisibility rules are rules that can help you to know if one whole number is divisible by another whole number. There are a number of divisibility rules.
Read more:
- Partitioning Explained For Elementary School Parents And Kids
- Free Division Worksheets For Elementary School: First to Fifth Grade
- Division Questions That Will Test Your Elementary School Students
Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.
Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.
Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring
Why not learn more about how it works?
The content in this article was originally written by primary school teacher Sophie Bartlett and has since been revised and adapted for US schools by elementary math teacher Christi Kulesza.





