The 12 Divisibility Rules You Should Know By Secondary School (Plus One That’s Totally New)

Divisibility rules are rules that help you to work out whether one number is divisible by another number exactly. This means that it leaves a whole number and doesn’t have any remaining numbers or decimals left over.

These rules are like a division process that can help you quickly work out whether a number is a multiple of another number. There are a number of these divisibility rules that can be very helpful when solving maths problems. Here we present 12 divisibility rules every maths student should know.

What are divisibility rules?

Divisibility rules are rules that help you know if a whole number can be divided by another whole number exactly (leaving no decimals), without having to go through a dividing procedure, such as long division or other division methods. 

Divisibility rules worksheet

Help your students prepare for their Maths GCSE with this free divisibility rules worksheet of 8 questions and answers.

Download Free Now!

Why do you need divisibility rules?

Divisibility rules are really useful for testing whether a number is a multiple of another or to help to check for prime numbers. They are useful when trying to simplify fractions or solve other problems involving large numbers.

When do you learn divisibility rules

In the UK, the divisibility rules for 2, 5 and 10 are normally taught in Year 2, with the rules for 3, 4and 8 being covered in Year 3, but there are more rules of division to learn throughout primary school and lots that are still very important in secondary school and beyond.

12 Divisibility Rules

Here we will list the most important divisibility rules that every student should know and some that aren’t as well known but very useful.

• Divisibility rule of 2 – Even numbers
• Divisibility rule of 3 – Sum of digits is a multiple of 3
• Divisibility rule of 4 – Last two digits are divisible by 4
• Divisibility rule of 5 – Last digit is a 5 or 0
• Divisibility rule of 6 – Divisible by 2 & 3
• Divisibility rule of 7 – Multiply the last digit by 2
• Divisibility rule of 8 – Half the number twice and see if that value is even
• Divisibility rule of 9 – Sum of its digits is a multiple of 9
• Divisibility rule of 10 – Last digit it 0
• Divisibility rule of 11 – Alternating sum of the digits multiple of 11
• Divisibility rule of 12 – Sum of digits is a multiple of 3 and last two digits are divisible by 4

Some of the divisibility rules rely on checking that the numbers are divisible by factors of that number, so more than one divisibility test may be required at times. Every integer is divisible by one so we’ll skip that! 

Later on we’ll also see why they are important in adult life!

See also: What is the highest common factor & What is the lowest common multiple

Divisibility rule of 2

A number is divisible by 2 if it is an even number. 

All even numbers have a last digit that is 0, 2, 4, 6, or 8.

Divisibility examples for 2:

478 ends with the digit 8, therefore 478 is even and is divisible by 2.

386519 ends with the digit 9, therefore 386519 is odd and not divisible by 2.

Divisibility rule of 3

To test if an integer is divisible by 3, we need to find the sum of the digits of the integer we are testing. If the sum of its digits is a multiple of 3, then the original integer is also a multiple of 3. If the sum of the digits is not an obvious multiple of 3, we can repeatedly add the digits of the sums until we can check if the number is a multiple of 3.

Divisibility examples for 3

126;

1+2+6=9. 9 is a multiple of 3, therefore 126 is divisible by 3.

76887694143612;

7+6+8+8+7+6+9+4+1+4+3+6+1+2=72,

7+2=9. 9 is a multiple of 3, therefore 76887694143612 is divisible by 3.

46736;

4+6+7+3+6=26. 

2+6=8. 8 is not a multiple of 3, therefore 46736 is not divisible by 3.

Divisibility rule of 4

For an integer to be divisible by 4, the first thing to do is check the last digit of the number is even, because 4 is an even number, any multiple of 4 will always be even.

If the last digit is even, we should now look at the last two digits. Checking to see if the last two digits are divisible by 4 is enough to see if any integer is divisible by 4. Why?

Well any integer larger than two digits will have at least a 100’s part. 

100 is 4 times 25 so any multiple of 100 will be divisible by 4. 

So if the remaining two digits are a multiple of 4, the whole number must also be a multiple of 4.

If you know your 4 times table, you can use this to check the last two digits

4, 8, 12, 16, 20, 24, 28, 32, 36, …

If you are not sure about the 4 times table past 48, then you can try halving the last two digits to see if that number is then even. If half of a number is even, then the original number must be a multiple of 4.

Divisibility examples for 4

4736 ends with 36. 36=4×9, so is divisible by 4, therefore 4736 is divisible by 4.

52678 ends with 78. 78÷2=39. 39 is odd, so 78 is not divisible by 4, therefore 52678 is not divisible by 4.

Divisibility rule of 5

The five times table produces values with a repeating pattern in the units digit. 

5, 10, 15, 20, 25, 30, 35, …

The multiples of 5 always end in a 0 or 5.

Divisibility examples for 5

47835 ends in a 5, therefore 47835 is divisible by 5.

6430 ends in a 0, therefore 6430 is divisible by 5.

783451 ends in a 1, therefore 783451 is not divisible by 5.

Divisibility rule of 6

To test if a given number is divisible by 6, we need to see if it passes divisibility tests for 2 and 3, because 2 and 3 are the prime factors of 6.

Divisibility examples for 6

456;

456 ends in a 6, which is even, therefore, 456 is divisible by 2.

4+5+6=15. 15 is divisible by 3, therefore, 456 is divisible by 3.

456 is divisible by both 2 and 3, therefore 456, is divisible by 6.

5372;

5372 ends in a 2, therefore, 5372 is divisible by 2.

5+3+7+2=17. 17 is not divisible by 3, therefore, 5372 is not divisible by 3.

5372 is divisible by 2 but not 3, therefore, 5372 is not divisible by 6.

Divisibility rule of 7 – an old rule and a brand new one!

Until recently the main divisibility test for 7 was as follows:

Multiply the last digit by 2 and then subtract from the rest of the number. If this value is a multiple of 7, the original number was a multiple of 7. The doubling and subtract process can be repeated for more steps if required.

Divisibility examples for 7 using subtraction

1659;

9×2=18, 165-18=147.

7×2=14, 14-14=0. 

0 is a multiple of 7,  therefore 1659 is divisible by 7.

New divisibility rule for 7

The new divisibility rule was discovered in 2019 by 12 year old Chika Ofili.

Chika discovered his rule while working on a summer holiday assignment.

Multiply the last digit by 5 and add this to the remaining digits, this process can be repeated if needed. If this value is a multiple of 7, the original number is divisible by 7.

Divisibility examples for 7 by multiplying by 5

8743;

3×5=15, 874+15=889.

9×5=45, 88+45=133.

3×5=15, 13+15=28.

28 is a multiple of 7, therefore 8743 is divisible by 7.

As well as discovering the rule, Chika also came up with an algebraic proof – what a promising young mathematician he is!

Divisibility rule of 8

For any integer to be divisible by 8, again we know it must be even. 

8=4×2=2×2×2, so we could half the number and check if that value is divisible by 4, or we could half the number twice and see if that value is even. These methods will work fine for numbers in the hundred or smaller but what about much larger numbers?

A method for larger integers is to use a similar process to the divisibility test for 4.

100 is not divisible by 8, but 1000 is divisible by 8 because 1000=8×125.

So to check if a larger number is divisible by 8, we only need to test the last three digits.

Divisibility examples for 8

245768 ends with 768. Half of 768 is 384, 84=4×21. So, 384 is divisible by 4, which means 768 is divisible by 8, therefore, 245768 is divisible by 8.

67892 ends with 892. Half of 892 is 446. 46 is not divisible by 4, so neither is 446. So 892 is not divisible by 8 and therefore, neither is 67892. 

Divisibility rule of 9

The divisibility test of 9 is similar to the test for 3.

To test if a number is divisible by 9 we need to check if the sum of its digits is a multiple of 9.

Like with the divisibility test for 3, we can keep repeating the process for each sum of the digits until the number is smaller.

Divisibility examples for 9

59364;

5+9+3+6+4=27. 27 is a multiple of 9, therefore, 59364 is divisible by 9.

358256;

3+5+8+2+5+6=29. 29 is not a multiple of 9, therefore, 358256 is not divisible by 9.

Divisibility rule of 10

Multiples of 10 will always have a zero as the units digit.

10, 20, 30, 40, 50, …..

Divisibility examples for 10

495430 ends in a 0, therefore 495430 is divisible by 10

6537 ends in 7, therefore is not divisible by 10.

Divisibility rule of 11

The divisibility rule of 11 is a little bit more complicated than the previous tests we have seen.

To test for numbers that are divisible by 11 we need to find the alternating sum of the digits. An alternating sum begins with a subtraction followed by an addition, then a subtraction, addition, and so on.

The alternating sum of the digits of 23456 would be 2-3+4-5+6=4.

If the alternating sum of the digits of a number is any multiple of 11 (positive, negative or zero), the original number is a multiple of 11.

Divisibility examples for 11

40194;

4-0+1-9+4=0. 0 is a multiple of 11, therefore, 40194 is divisible by 11.

5978321;

5-9+7-8+3-2+1=-1. -1 is not a multiple of 11, therefore, 5978321 is not divisible by 11.

Divisibility rule of 12

To test if a number is divisible by 12, we need to see if it passes the test for 3 and the test for 4, because 12 is a composite number.

Divisibility examples for 12

42816;

4+2+8+1+6=21. 21 is a multiple of 3, so 42816 is divisible by 3.

42816 ends in 16. 16 is divisible by 4, so 42816 is divisible by 4.

Therefore, 42816 is divisible by 12.

How can I find other divisibility rules?

We’ve seen that the divisibility tests for 6 and 12 consisted of using the tests for 2, 3 and 4. This is because 6 and 12 are composite numbers meaning they are made from more than one prime factor.

6=2×3

12=2^{2}×3

So, divisibility tests for other composite numbers can consist of the tests of the prime factors to their largest power.

Examples of divisibility 

15= 3×5, so to test divisibility by 15, we can test for 3 and 5.

18= 2×3^{2}=2×9, so to test divisibility by 18, we can test for 2 and 9.

24= 2^{3}×3=8×3, so to test divisibility by 24, we can test for 3 and 8.

45= 3^{2}×5=9×5, so to test divisibility by 45, we can test for 9 and 5.

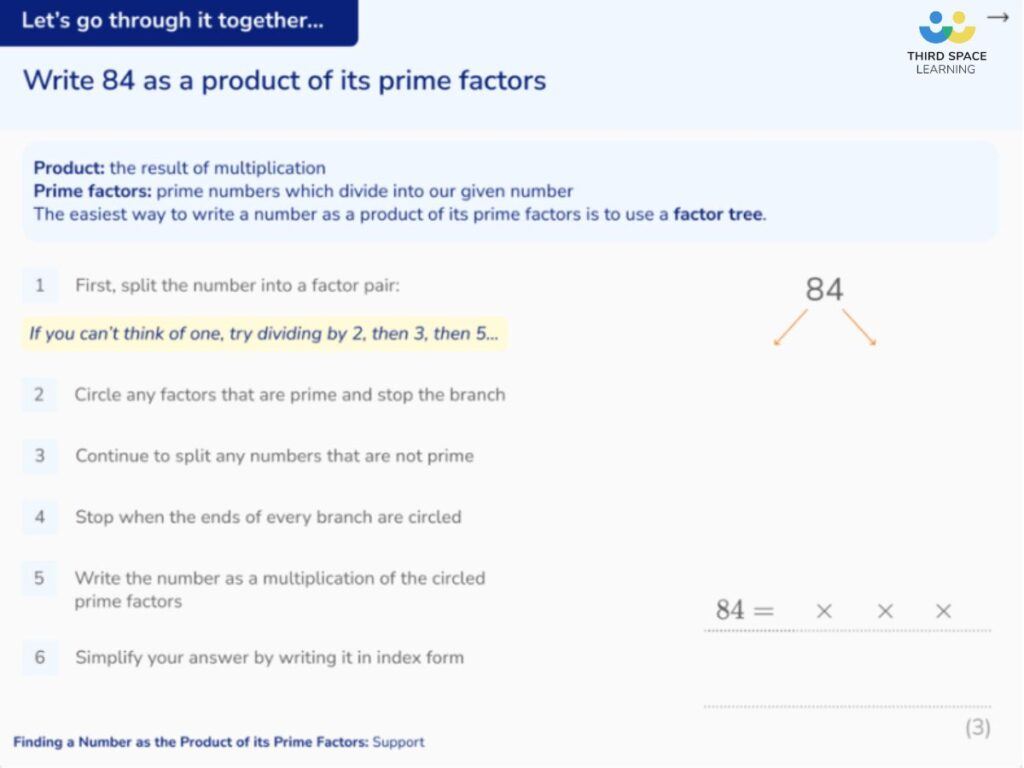
84=2^{2}×3×7=4×3×7 , so to test divisibility by 84, we can test for 4, 3 and 7.

So in general, to check for divisibility by a number N, we need to check for divisibility by the highest power of each of the prime factors of N.

What about divisibility rules for other large prime numbers?

The divisibility tests for some larger prime numbers and more than a two-digit number can be quite complicated. But regardless of the number of digits, such numbers have a similar process to the divisibility rule for 7. There is also a general rule which applies for testing all other prime numbers ending in a 1, 3, 7 or 9.

Third Space Learning’s online one-to-one tuition encourages students to identify number patterns and apply their knowledge to solve maths problems.

Here are some interesting rules for larger prime numbers:

Divisibility rule for 29 – Multiply the last digit by 3 and add it to the remaining truncated number. Repeat this step if necessary. If the result is divisible by 29, the original number is also divisible by 29.

Divisibility rule for 41 – Multiply the last digit by 4 and subtract from the remaining truncated number. Repeat this step if necessary. If the result is divisible by 41, the original number is also divisible by 41.

Do divisibility rules only matter in school?

Prime numbers and divisibility are a large part of the mathematical field of Number Theory. There are many important theorems and a huge amount of research goes into this area of mathematics which is vital for applications such as cryptography, internet and device security and e-commerce, which are all very profitable industries to work in. 

Getting students interested in number theory at an early age could set them up for life! 

1. Which of the following is 2648 divisible?

12

6

8

9

2 + 6 + 4 + 8 = 20, therefore it is not divisible by 3, 6, 12 or 9.

2. Which two divisibility tests can be used to test for divisibility by 72?

8 and 9

6 and 12

4 and 9

3 and 2

To check for divisibility by a number N, we need to check for divisibility by the highest power of each of the prime factors of N. 72=2^{3}×3^{2}.

3. Which of the following numbers is divisible by 11?

1513

1235

2576

1727

1-7+2-7=-11. The alternating sum is a multiple of 11.

4. Which of the following is divisible by 7?

2280

6615

3519

9234

661-25=651, 65-21=63. 63 is a multiple of 7 so 6615 is divisible by 7.

5. 6930 is divisible by which set of numbers?

4, 5, 11

2, 5, 9

9, 10, 12

3, 5, 8

6930, is even, ends in a 0 and 6 + 9 + 3 + 0 = 18, therefore it is divisible by 2, 5 and 9.

A number 584ꪛ2 has a missing digit ꪛ. The number is divisible by 4 but not 8. What is the missing digit?

3

7

9

6

92 is divisible by 4. 492 is not divisible by 8.

Divisibility rules FAQs