What Are Factors And Multiples? Explained For Primary School
Factors and multiples are usually taught together: whilst factors are the result when you divide a number by an integer (whole number) with no remainder, multiples are the result when you multiply a number by an integer. Children often get the two confused, although they will be introduced to multiples from Year 1, they won’t learn about factors until Year 4.
- What are factors and multiples?
- What are common multiples?
- What are common factors?
- What is the difference between factors and multiples?
- How to find factors and multiples
- When do children learn about factors and multiples in school?
- How do factors and multiples relate to other areas of maths?
- How do factors and multiples link to real life?
- Factors and multiples worked examples
- Factors and multiples practise questions
Factors, Multiples, Square & Cube Numbers Pack
Download this pack to teach pupils how to identify factors, common factors, prime numbers, multiples and common multiples. Includes pupil practice sheets!
Download Free Now!What are factors and multiples?
Factors
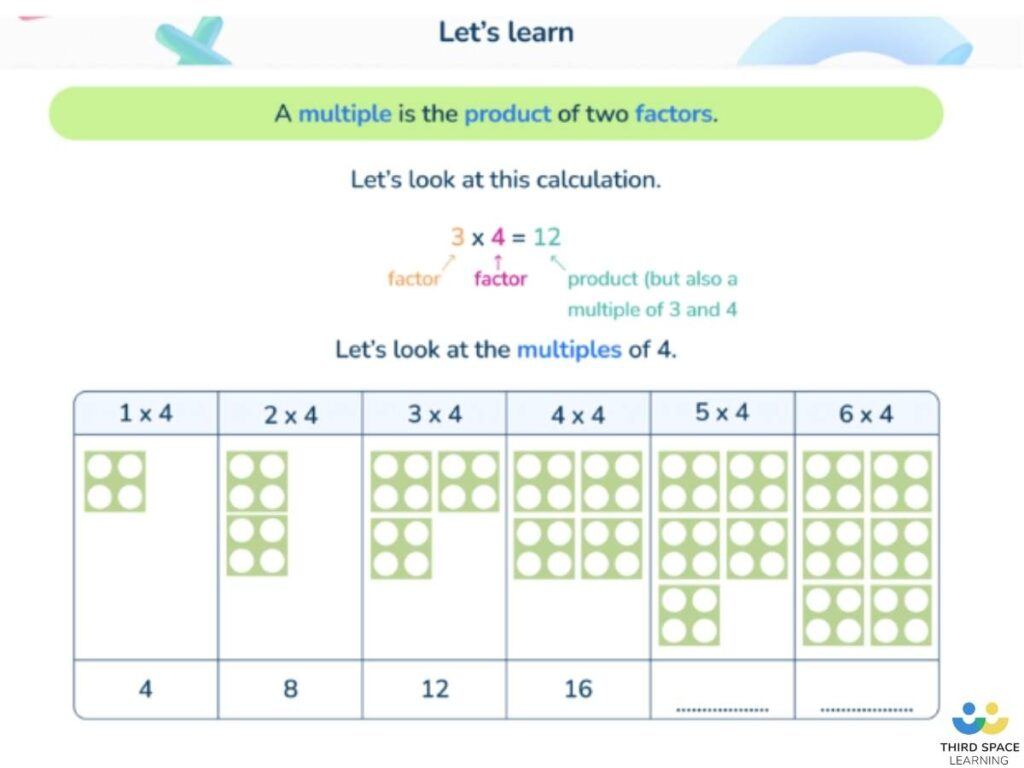
A factor is a number that fits exactly into a given number, or divides into a particular number with no remainder (fraction or decimal). Factors can also be identified as two or more numbers that multiply together to make another number. A factor is always a positive integer.
For example, 4 is a factor of 8, 12, 16, 20, etc. because 8 ÷ 4 = 2, 12 ÷ 4 = 3, 16 ÷ 4 = 4, 20 ÷ 4 = 5, etc.; therefore, all the numbers in the 4 times tables have 4 as a factor.
To find the factors of a number, it’s useful to look for them in pairs as two factors will multiply to make another number. The factor pairs of 12 are 1 x 12, 2 x 6 and 3 x 4, so the factors of 12 are 1, 2, 3, 4, 6 and 12. Prime numbers can be defined by their factors – they only have two (1 and themself).
Multiples
What is a multiple? A multiple of a number is the result when that number is multiplied by an integer. Compared to the factor examples above, whereas 4 is a factor of 8 and 12, 8 and 12 are multiples of 4.
Other examples of multiples of 4 could be 4 (4 x 1), 36 (4 x 9) or 400 (4 x 100). Multiples can also be described as numbers in a given times table – for example, 4, 8, 12 and 16 are all in the 4 times table; they are also all multiples of 4. There is a multiple of every number.
What are common multiples?
Common multiples are multiples shared between two or more given numbers. For example, 24 is a common multiple of 2, 3 and 6 as it is a multiple of all three numbers (note that 2, 3 and 6 are therefore all factors of 24).
The lowest common multiple (LCM), also referred to as the least common multiple, is the smallest multiple shared between two or more given numbers. For example, the lowest common multiple of 10 and 15 is 30 as it is the smallest multiple that both given numbers share (10 x 3 = 30 and 15 x 2 = 30). Lowest common multiples can be used to express fractions in the same denomination, which is useful when they are being added or subtracted.
What are common factors?
Common factors are factors shared between two or more given numbers. For example, 5 is a common factor of 5, 10 and 25 as it is a factor of all three numbers (note that 5, 10 and 25 are therefore all multiples of 5).
The highest common factor (HCF), also referred to as the greatest common factor, is the largest factor shared between two given numbers. For example, the highest common factor of 15 and 20 is 5 as it is the largest number that both given numbers can be divided by without remainders. Highest common factors can be used to simplify fractions.
What is the difference between factors and multiples?
A factor of a given number is smaller than that number, but a multiple of a given number is bigger. Every number has a set amount of factors (the minimum being two factors – these are called prime numbers), but an infinite amount of multiples – this is because we can just keep multiplying forever!
How to find factors and multiples
Every number has a set amount of factors. Firstly, every number has a factor of 1. Numbers with only two factors (1 and themselves) are called prime numbers. Numbers with more than two factors are called composite numbers. There are a few ways to find all the factors of a given number.
Some factors are easy to spot – for example, if a number ends in a 0 or 5, then 5 must be a factor; if a number is even, then 2 must be a factor. See more division tricks here to work out whether a number has a factor of 2, 3, 4, 5, 6, 8, 9 or 10!
To find all the factors of a given number, start with 1 and systematically work through each number to see if it has a factor pair that will multiply to make the given number, until the factors end up repeating themselves. For example, to find all the factors of 24:

There is no point continuing from 12 as 12 is half of 24, so any number bigger will not have a factor pair other than 1. The factors of 24 are therefore 1, 2, 3, 4, 6, 8 and 12. These can be represented a number of ways, including factor ‘rainbows’, factor ‘bugs’ or arrays.
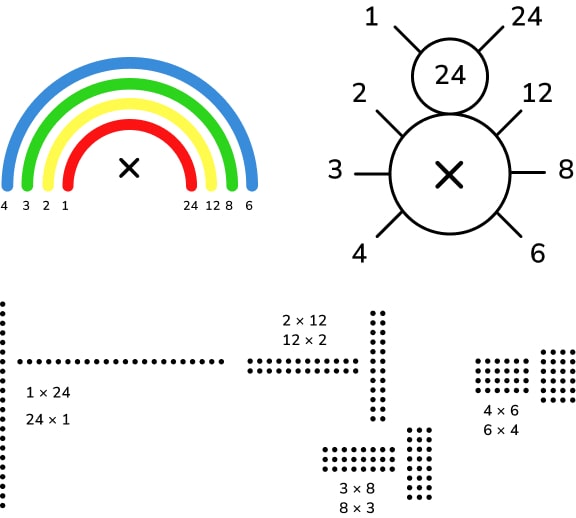
Multiples are a lot more simple to find. To find any multiple of a given number, multiple the number by another integer – the result is a multiple of that number.
See also: grid method multiplication
When do children learn about factors and multiples in school?
Children are expected to know the first 12 multiples of the numbers 1-12 by the end of Year 4. This is gradually taught from:
- Year 1 – count in multiples of twos, fives and tens
- Year 2 – count in steps of 2, 3, and 5 from 0, and in tens from any number, forward and backward
- Year 3 – count from 0 in multiples of 4, 8, 50 and 100
- Year 4 – count in multiples of 6, 7, 9, 25 and 1000
Factors and multiples is such a key topic that it even appears in GCSE.
Pupils will first encounter factors, and multiples in other contexts, in Key Stage 2, where in Year 4 they will:
- recognise and use factor pairs and commutativity in mental calculations
- use factors and multiples to recognise equivalent fractions and simplify where appropriate
In Year 5, children will:
- identify multiples and factors, including finding all factor pairs of a number, and common factors of two numbers
- know and use the vocabulary of prime numbers, prime factors and composite numbers
- solve problems involving multiplication and division including using their knowledge of factors and multiples, square numbers and cube numbers
And finally in Year 6, children will be expected to:
- identify common factors, common multiples and prime numbers
- use common factors to simplify fractions
- use common multiples to express fractions in the same denomination
- solve problems involving unequal sharing and grouping using knowledge of fractions and multiples
See also: Long multiplication method & Long multiplication
How do factors and multiples relate to other areas of maths?
Factors are useful when discussing the area of a rectangle or volume of a cuboid, e.g. a rectangle with an area of 12cm^2 could have the dimensions 1 cm x 12cm, 2cm x 6cm or 3cm x 4cm as these are all factor pairs of 12.
Common factors can be used when simplifying fractions, e.g. 12/15 simplified is ⅘ (3 is a common factor of both the numerator and the denominator).
In Year 5 geometry, children are taught multiples of 90 degrees (90 = quarter turn; 180 = half a turn, or a straight line; 270 = three-quarter turn; 360 = full turn, or a circle).
Common multiples are useful when expressing fractions in the same denomination, e.g. ⅔ + ¾ can be turned into 8/12 + 9/12 (the new denominator, 12, is a common multiple of both the original denominators, 3 and 4).
How do factors and multiples link to real life?
Factors can be used when organising a number into groups – for example, a group of 12 people could be split into 2 groups of 6, 2 groups of 4, 4 groups of 3 or 6 groups of 2.
Multiples can also be used to organise a number into groups – for example, 30 is a multiple of 10: 30 children could be organised into groups of 10; 30p could be paid in 10ps; 30 flowers could be planted in rows of 10.
Common multiples are also useful in real life contexts – for example, if sausages come in packs of 6, but hot-dog buns come in packs of 4, finding a common multiple (12) would help you work out how many of each pack to buy (2 and 3 respectively) without wasting any.
Factors and multiples worked examples
- Write three factors of 30 that are not factors of 15
The factors of 30 are 1, 2, 3, 5, 6, 10, 15 and 30. The factors of 15 are 1, 3, 5 and 15. So the factors of 30 that aren’t the factors of 15 are 2, 6, 10 and 30 – you could pick any three of these. - Here are 4 digits: 7, 5, 2 and 1. Choose 2 digits each time to make the following numbers. The first one is done for you:
– an even number: 52
– a multiple of 9: _ _
– a square number: _ _
– a factor of 96: _ _
A multiple of 9 could be 72 or 27 (in multiples of 9, the digits add to 9, which makes it easier to spot!)
A square number is 25 (5 x 5 = 25) – this is the only possible answer
A factor of 96 is 12 – this is the only possible answer - White balloons come in bags of 24. Red balloons come in bags of 12. Molly buys 6 bags of white balloons. Saad buys 3 bags of red balloons. Molly says, ‘I have 4 times as many balloons as Saad’. Explain why Molly is correct.
24 (bag of white balloons) is double 12 (bag of red balloons), and 6 (bags of white being bought) is double 3 (bags of red being bought). This means overall, the amount will be 4 times as large. Also, 24 x 6 = 144, 12 x 3 = 36 and 144 balloons is 4 times as many as 36 balloons.
Looking for more factors and multiples resources? Third Space Learning offers an extensive library of worksheets including both premium and free resources. In addition to our learning and teaching resources, Third Space Learning’s online one-to-one tuition provides students with the personalised maths programme they need to grow their skills and confidence in maths.
For more resources, take a look at our collection of KS2 multiplication worksheets.
Factors and multiples practise questions
- The factors of 11 sum to 12. Write the other number whose factors sum to 12. Answer: 6 – the factors are 1, 2, 3 and 6.
- Write all the numbers between 50 and 100 that are factors of 180. Answer: 60 and 90
- Write all the common multiples of 3 and 8 that are less than 50. Answer: 24 and 48
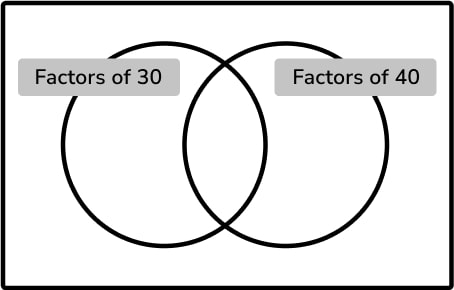
- Write these numbers in the correct places on the diagram: 5, 6, 7 and 8. Answer: factors of 30 = 6; factors of 40 = 8; factors of 30 and 40 (overlap) = 5; outside circles = 7
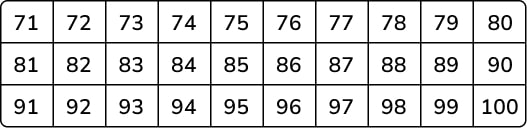
5. Here is a number chart. Circle the smallest number on the chart that is a multiple of both 2 and 7. Answer: 84
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s maths specialist tutors support thousands of students across hundreds of schools with weekly online maths tuition designed to plug gaps and boost progress.
Since 2013 these personalised one to one lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.
Learn about the scaffolded lesson content or request a personalised quote for your school to speak to us about your school’s needs and how we can help.