What Is A Square Number? Explained For Primary School Parents And Kids
In this post we will be explaining what square numbers are, why they are called square numbers and providing all the information you’ll need to help your child get to grips with this area of maths. We’ve also included some square number based questions for your child to tackle, so take a look!
What is a square number?
A square number is the result when a number has been multiplied by itself. For example, 25 is a square number because it’s 5 lots of 5, or 5 x 5. This is also written as 52 (“five squared”). 100 is also a square number because it’s 102 (10 x 10, or “ten squared”).
Square number examples
5 examples of square numbers are 625 (25 x 25, 252), 90,000 (300 x 300, 3002), 289 (17 x 17, 172), 1 (1 x 1, 12) and 2304 (48 x 48, 482)
FREE Factors, Multiples, Square & Cube Numbers Pack
Download this resource pack aimed at helping pupils identify number properties and relationships in advance of SATs. It includes teaching guidance, pupil practice sheets and activity slides.
Download Free Now!Square numbers up to 12 x 12
The first 12 square numbers (and the ones children are most likely to know due to learning their times tables) are:
1 x 1 or 12 = 1
2 x 2 or 22 = 4
3 x 3 or 32 = 9
4 x 4 or 42 = 16
5 x 5 or 52 = 25
6 x 6 or 62 = 36
7 x 7 or 72 = 49
8 x 8 or 82 = 64
9 x 9 or 92 = 81
10 x 10 or 102 = 100
11 x 11 or 112 = 121
12 x 12 or 122 = 144
The square numbers from 1 to 100 are: 1, 4, 9, 25, 36, 49, 64, 81, 100
Here’s a handy image you can save with the above information on: 
How do you square a number?
This is very simple. All you have to do is take the number, and multiply it by itself!
Why are they called ‘square’ numbers?
What are ‘square’ numbers? Why are they not called (insert shape here) numbers?
These are questions that many primary school children ask, but fortunately the answer is simple. These particular collection of numbers are called square numbers (or squared numbers) for the simple reason that they form the area of a square. As squares have equal sides, calculating the area is simple – just “square” (multiply by itself) one of its sides!
For example, a square with side length 2cm would have an area of 4cm2 (as 22 = 4). In reverse, if we knew a square had an area of 9cm2, we’d know that each side would measure 3cm (as 32 = 9). See the diagrams below to demonstrate these examples.
You could use a 100 square to show this!
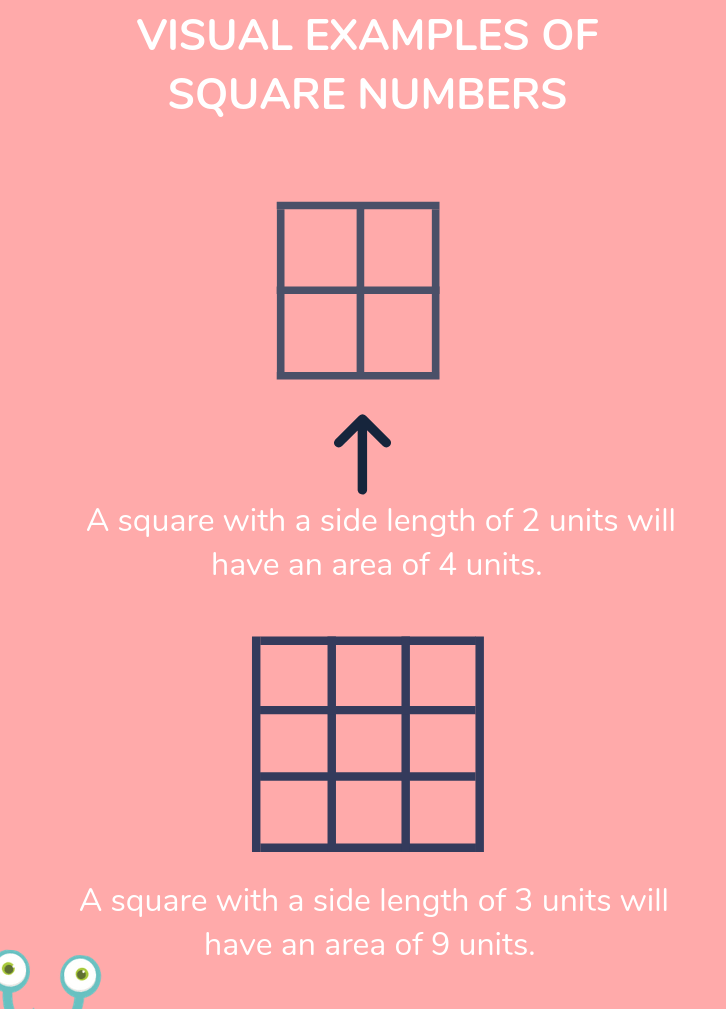
Square numbers for kids: When will my child learn about square numbers in primary school?
Whilst your child may learn about square numbers earlier, the National Curriculum doesn’t require schools to introduce square numbers until Year 5. As part of the multiplication and division topic, the curriculum states that pupils should be taught to:
- recognise and use square numbers and cube numbers, and the notation for squared (2) and cubed (3)
- solve problems involving multiplication and division including using their knowledge of factors and multiples, squares and cubes
In the non-statutory notes and guidance, the curriculum advises that children understand the terms factor, multiple and prime, square and cube numbers and use them to construct equivalence statements (for example, 4 x 35 = 2 x 2 x 35; 3 x 270 = 3 x 3 x 9 x 10 = 92 x 10).
See also: What are factors?
This knowledge will be built on in Year 6, particularly when learning about the order of operations, when children may learn the term ‘indices’ (an ‘index number’ is the name for the little 2 used to mean ‘squared’, or the little 3 used to mean ‘cubed’). By Year 5 and Year 6, children are expected to know not only the square numbers up to 12 x 12, but also the square numbers of multiples of 10 (20 x 20 = 400, 30 x 30 = 900 etc.)
How do square numbers relate to other areas of maths?
Square numbers are particularly useful when finding the area of squares, which children begin to do in Year 4 (pupils should be taught to find the area of rectilinear shapes by counting squares) but which is built on further in Year 5 (pupils should be taught to calculate and compare the area of rectangles (including squares).
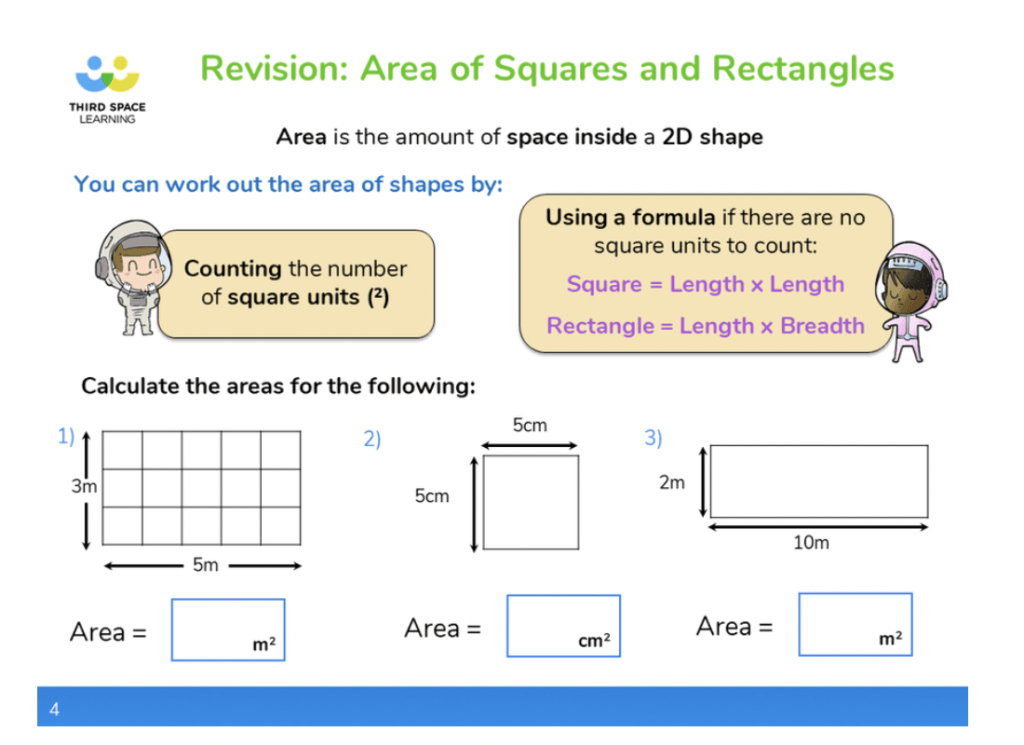
As previously mentioned, knowledge of square numbers is built on in Year 6 when pupils should be taught to use their knowledge of the order of operations (BODMAS) to carry out calculations.
Learning square numbers also gives children a firm base from which they can learn about cube or cubed numbers, but this will not usually happen until KS3.
Wondering about how to explain other key maths vocabulary to your children? Check out our Primary Maths Dictionary For Kids, or try these primary maths terms:
- What Is Long Multiplication: Explained For Primary Parents And Kids
- What Is The Lowest Common Multiple: Explained For Primary Parents And Kids
- What Is The Highest Common Factor: Explained For Primary Parents And Kids
Square number practice questions
1) 72 =
2) 36 and 64 are both square numbers. They have a sum of 100. Find two square numbers that have a sum of 130.
3) Here is a sorting diagram for numbers. Write a number less than 100 in each space.

4) Explain why 16 is a square number.
5) A question from the 2019 KS2 maths SATs paper testing children’s application of their knowledge of square numbers:

All of our resources for primary schools can be found in the Third Space Maths Hub
Create your own free Maths Hub account to access hundreds of free resources, guides and CPD videos. Premium Maths Hub access includes 36 weeks of Fluent in Five, Rapid Reasoning and Ready To Go Lesson Slides for years 1 to 6. It is available through a whole-school subscription or is included at no additional cost for schools using our online one to one maths tutoring.
Register free for the Third Space Maths Hub.
Enquire about Premium Maths Hub
Square number worksheets
- Ready-to-go lessons Year 5 Multiplication and Division (Autumn Block 4) Slides and Worksheets
- Ready-to-go lessons Year 6 4 Operations (Autumn Block 2) Slides and Worksheets
- Year 5 Worked Examples Worksheet: Multiplication and Division 1
- Year 6 Worked Examples Worksheet: Four Operations
Square number videos
DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?
Every week Third Space Learning’s maths specialist tutors support thousands of students across hundreds of schools with weekly online maths tuition designed to plug gaps and boost progress.
Since 2013 these personalised one to one lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.
Learn about the scaffolded lesson content or request a personalised quote for your school to speak to us about your school’s needs and how we can help.