![How To Teach Division KS2: Maths Bootcamp [7]](https://thirdspacelearning.com/wp-content/uploads/2020/05/Resized/how-teach-division-ks2-bootcamp-150x150.jpg)
What Are Cube Numbers? Explained for Primary School Teachers, Parents and Kids
Here you can find out what cube numbers are, why they are called cube numbers and how you can help children to understand cube numbers as part of their maths learning at home.
What is a cube number?
A cube number is the result when a number has been multiplied by itself twice. The symbol for cubed is 3.
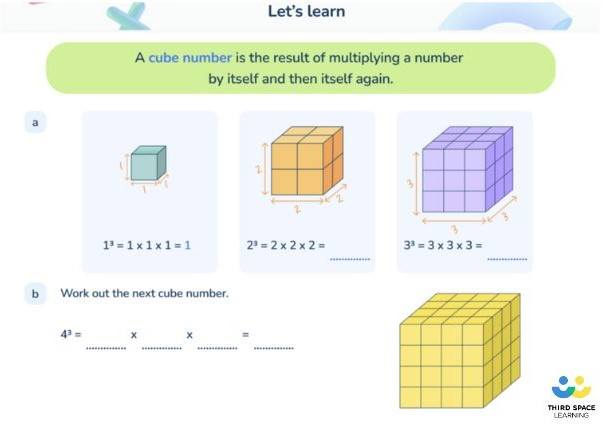
For example, 8 is a cube number because it’s 2 x 2 x 2 (2 multiplied by itself twice); this is also written as 23 (“two cubed”).
Another example of a cube number is 27 because it’s 33 (3 x 3 x 3, or “three cubed”).
A cube number can also be called a number cubed.
- 2³ = 2 × 2 × 2 = 8
- 3³ = 3 × 3 × 3 = 27
- 4³ = 4 × 4 × 4 = 64
- 5³ = 5 × 5 × 5 = 125
Cube numbers
Watch this video to find out how to teach cube numbers and square numbers to primary aged children.
List of cube numbers up to 10 x 10 x 10
The first 10 cube numbers are:
1 = 1 x 1 x 1 or 13
8 = 2 x 2 x 2 or 23
27 = 3 x 3 x 3 or 33
64 = 4 x 4 x 4 or 43
125 = 5 x 5 x 5 or 53
216 = 6 x 6 x 6 or 63
343 = 7 x 7 x 7 or 73
512 = 8 x 8 x 8 or 83
729 = 9 x 9 x 9 or 93
1,000 = 10 x 10 x 10 or 103
The cube numbers from 1 to 100 are: 1, 8, 27, 64
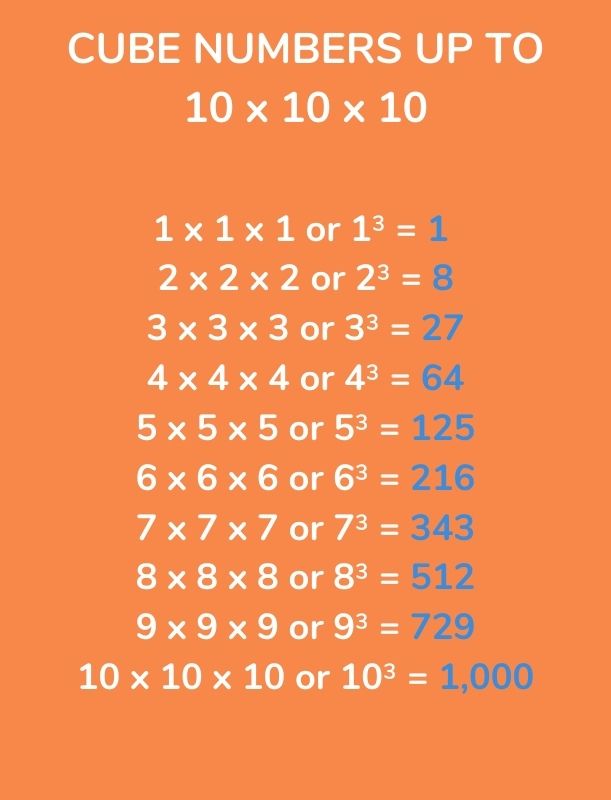
FREE Factors, Multiples, Square & Cube Numbers Pack
Download this resource pack aimed at helping pupils identify number properties and relationships in advance of SATs. It includes teaching guidance, pupil practice sheets and activity slides.
How to cube a number
To cube a number all you do is multiply it by itself twice. This works for all numbers.
So for example 11 cubed is 113 or 11 x 11 x 11 which is 1331.
Another example could be 2563 or 256 x 256 x 256 which is 16,777,216
As you can see when you cube a whole number, you’ll find the numbers get very big very quickly!
Why are they called cube numbers
They are named cube numbers (or cubed numbers) because they can also be used to calculate the volume of a cube: since a cube is a 3d shape with sides of the same length, width and height, you calculate its volume by multiplying the side length by itself twice (or ‘cubing’ it).
As cubes have equal sides (length, height and width), calculating the volume is simple – just “cube” (multiply by itself twice) one of its sides!
For example, a cube with side length 2cm would have a volume of 8cm3 (as 23 = 8). In reverse, if we knew a cube had a volume of 27cm3, we’d know that each side would measure 3cm (as 33 = 27).
See the diagrams below to demonstrate these cube number examples.
- A cube with side length 2 units, volume 8 units ie 2 x 2 x 2 – we can also see there are 8 cubes.
2. A cube with side length 3 units, volume 27 units ie 3 x 3 x 3 – we can also see there are 27 cubes)
When will children learn about cube numbers in primary school?
As part of the multiplication and division topic, the national curriculum for Key Stage 2 states that Year 5 pupils should be taught to:
- recognise and use square numbers and cube numbers, and the notation for squared (2) and cubed (3)
- solve problems involving multiplication and division including using their knowledge of factors and multiples, squares and cubes
In the non-statutory notes and guidance, the curriculum advises that children understand the terms factor, multiple and prime, square and cube numbers and use them to construct equivalence statements (for example, 4 x 35 = 2 x 2 x 35; 3 x 270 = 3 x 3 x 9 x 10 = 92 x 10).
This knowledge of square numbers will be built on in Year 6, particularly when learning about BIDMAS and the order of operations when children may learn the term ‘indices’ (an ‘index number’ is the name for the little 2 used to mean ‘squared’, or the little 3 used to mean ‘cubed’).
Cube roots, like square roots, or working with squares and cubes of decimals are not generally tackled by children until secondary school closer to GCSE.
How do cube numbers relate to other areas of maths?
Cube numbers are particularly useful when finding the volume of cubes, which children begin to do in Year 5 (pupils should be taught to estimate volume [for example, using 1cm3 blocks to build cuboids (including cubes)])
In Year 6, pupils should be taught to calculate, estimate and compare volume of cubes and cuboids using standard units, including cubic centimetres (cm3) and cubic metres (m3), and extending to other units [for example, mm3 and km3].
By Year 6 maths pupils will be taught to use their knowledge of the order of operations to carry out calculations and problem solving questions with cubed numbers, including two-step and multi-step word problems.
Wondering how to explain other key numeracy vocabulary to your children? Check out our Maths Dictionary For Kids, or try the following explanations for parents of children following a maths mastery approach in their primary school:
- What Is The Lowest Common Multiple?
- What Is The Highest Common Factor?
- What Are Prime Numbers?
- What Is Place Value?
Cube number questions and answers
1. Order these from smallest to largest: 52 32 33 23
(Answer: 23 (8), 32 (9), 52 (25), 33 (27))
2. Which of these numbers are also square numbers? 13 23 33 43 53
(Answer: 13 (1), 43 (64))
3. Find two cube numbers that total 152.
(Answer: 125 (53) + 27 (33))
4. Write a number less than 100 in each space in this sorting diagram.
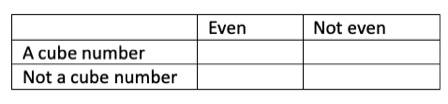
Answer:
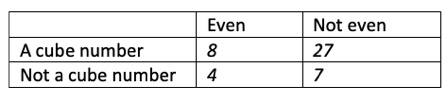
5. Explain why 125 is a cube number.
(Answer: Because it’s 5 x 5 x 5, or 53)Cube number questions and answers
Cube numbers worksheet
Online 1-to-1 maths lessons trusted by schools and teachers
Every week Third Space Learning’s maths specialist tutors support thousands of primary school children with weekly online 1-to-1 lessons and maths interventions. Since 2013 we’ve helped over 130,000 children become more confident, able mathematicians. Learn more or request a personalised quote to speak to us about your needs and how we can help.
| Primary school tuition targeted to the needs of each child and closely following the National Curriculum. |
