What Are Cube Numbers? Explained For Elementary School

Here you can find out what cube numbers are, why they are called cube numbers and how you can help children to understand cube numbers.

What is a cube number?

A cube number is found when we multiply a number by itself and then itself again. The symbol for cubed is ³.

For example, 8 is a cube number because it’s 2 x 2 x 2; this is also written as 2³ (“two cubed”).

Another example of a cube number is 27 because it’s 3³ (3 x 3 x 3, or “three cubed”).

A cube number can also be called a number cubed.

• 2³ = 2 × 2 × 2 = 8
• 3³ = 3 × 3 × 3 = 27
• 4³ = 4 × 4 × 4 = 64
• 5³ = 5 × 5 × 5 = 125

List of cube numbers up to 10 x 10 x 10

The first 10 cube numbers are:

1 = 1 x 1 x 1 or 1³

8 = 2 x 2 x 2 or 2³

27 = 3 x 3 x 3 or 3³

64 = 4 x 4 x 4 or 4³

125 = 5 x 5 x 5 or 5³

216 = 6 x 6 x 6 or 6³

343 = 7 x 7 x 7 or 7³

512 = 8 x 8 x 8 or 8³

729 = 9 x 9 x 9 or 9³

1,000 = 10 x 10 x 10 or 10³

The cube numbers from 1 to 100 are: 1, 8, 27, 64

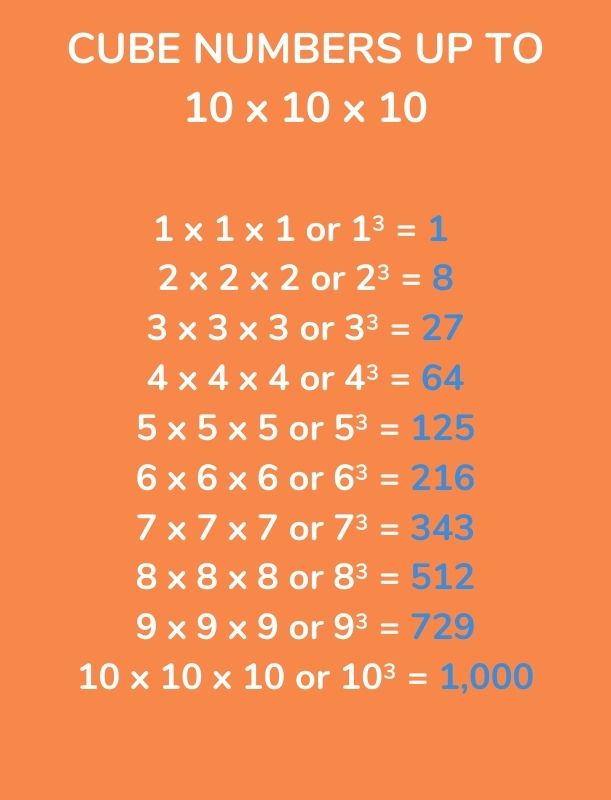
How to cube a number

To cube a number all you do is multiply it and by itself and then itself again. This works for all numbers.

So for example 11 cubed is 11³ or 11 x 11 x 11 which is 1331.

Another example could be 256³ or 256 x 256 x 256 which is 16,777,216

As you can see when you cube a whole number, you’ll find the numbers get very big very quickly!

Why are they called cube numbers?

They are named cube numbers (or cubed numbers) because they can also be used to calculate the volume of a cube: since a cube is a 3d shape with sides of the same length, width and height, you calculate its volume by multiplying the side length by itself and then itself again (or ‘cubing’ it).

As cubes have equal sides (length, height and width), calculating the volume is simple – just “cube” one of its sides!

For example, a cube with side length 2in would have a volume of 8in³ (as 2³ = 8). In reverse, if we knew a cube had a volume of 27in³, we’d know that each side would measure 3in (as 3³ = 27).

See the diagrams below to demonstrate these cube number examples.

1. A cube with side length 2 units, volume 8 units ie 2 x 2 x 2 – we can also see there are 8 cubes.

2. A cube with side length 3 units, volume 27 units ie 3 x 3 x 3 – we can also see there are 27 cubes)

When do children learn about cube numbers in elementary school?

As part of the multiplication and division topic, the Common Core math states that by 4th grade students should be taught to:

• recognize and use square numbers and cube numbers, and the notation for squared (²) and cubed (³)
• solve problems involving multiplication and division including using their knowledge of factors and multiples, squares and cubes

Children should understand the terms factor, multiple and prime, square and cube numbers and use them to construct equivalence statements (for example, 4 x 35 = 2 x 2 x 35; 3 x 270 = 3 x 3 x 9 x 10 = 92 x 10).

This knowledge of square numbers will be built on, particularly when learning about PEMDAS (also known as BODMAS) and the order of operations when children may learn the term ‘exponent’ (the name for the little 2 used to mean ‘squared’, or the little 3 used to mean ‘cubed’).

Cube roots, like square roots, or working with squares and cubes of decimals are not generally tackled by children until middle school or even high school.

How do cube numbers relate to other areas of math?

Cube numbers are particularly useful when finding the volume of cubes, which children begin to do in 4th grade (students should be taught to estimate volume [for example, using 1in³ blocks to build cuboids including cubes])

In 5th grade, pupils should be taught to calculate, estimate and compare volume of cubes and cuboids using standard units, including cubic inches (in³) and cubic feet (ft³), and extending to other units.

By 5th grade math pupils will be taught to use their knowledge of the order of operations to carry out calculations and problem solving questions with cubed numbers, including two-step and multi-step word problems.

Wondering how to explain other key numeracy vocabulary to children? Check out our Math Dictionary For Kids, or try the following explanations for parents of children following a math mastery approach in their primary school:

• What Is The Lowest Common Multiple?
• What Is The Highest Common Factor?
• What Are Prime Numbers?
• What Is Place Value?

Cube number questions and answers

1. Order these from smallest to largest: 5² 3²   3³   2³  

(Answer: 2³ (8), 3² (9), 5² (25), 3³ (27))

2. Which of these numbers are also square numbers? 1³   2³   3³   4³   5³

(Answer: 1³ (1), 4³ (64))

3. Find two cube numbers that total 152.

(Answer: 125 (5³) + 27 (3³))

4. Write a number less than 100 in each space in this sorting diagram.

Answer:

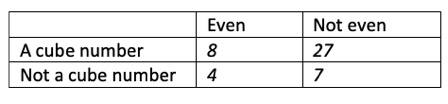
5. Explain why 125 is a cube number.

(Answer: Because it’s 5 x 5 x 5, or 5³)

Do you have students who need extra support in math?
Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor.

Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way.

Personalized one-on-one math tutoring programs are available for:
– 2nd grade tutoring
– 3rd grade tutoring
– 4th grade tutoring
– 5th grade tutoring
– 6th grade tutoring
– 7th grade tutoring
– 8th grade tutoring

Why not learn more about how it works?

The content in this article was originally written by primary school teacher Sophie Bartlett and has since been revised and adapted for US schools by elementary math teacher Katie Keeton.