What Is PEMDAS? Explained For Kids, Parents & Teachers

PEMDAS pops up across elementary and middle school and is a popular acronym used to help students remember the order of operations. In this article, we explain what PEMDAS means, provide you with worked examples and practice questions to support your students in the classroom.

What is PEMDAS?

PEMDAS is a well-known acronym used to help students remember the order of operations. 

PEMDAS stands for:

• Parentheses
• Exponents
• Multiplication 
• Division
• Addition
• Subtraction

What is the PEMDAS rule?

The PEMDAS rule tells students how to solve math problems with multiple operations and in which order they should be completed in order to produce the correct answer. 

It is important to note that the inverse operations multiplication and division, as well as addition and subtraction, are interchangeable within this list, and are performed from left to right as they appear within an expression. 

To avoid confusion, some teachers prefer to display PEMDAS as shown below, with M/D (for multiplication and division) and A/S (for addition and subtraction) at the same level:

P	Parentheses: (  ) [  ] {  }
E	Exponents: 22 43
M/D	Multiplication and Division:  x  ÷ from left to right
A/S	Addition and Subtraction:  +  –from left to right

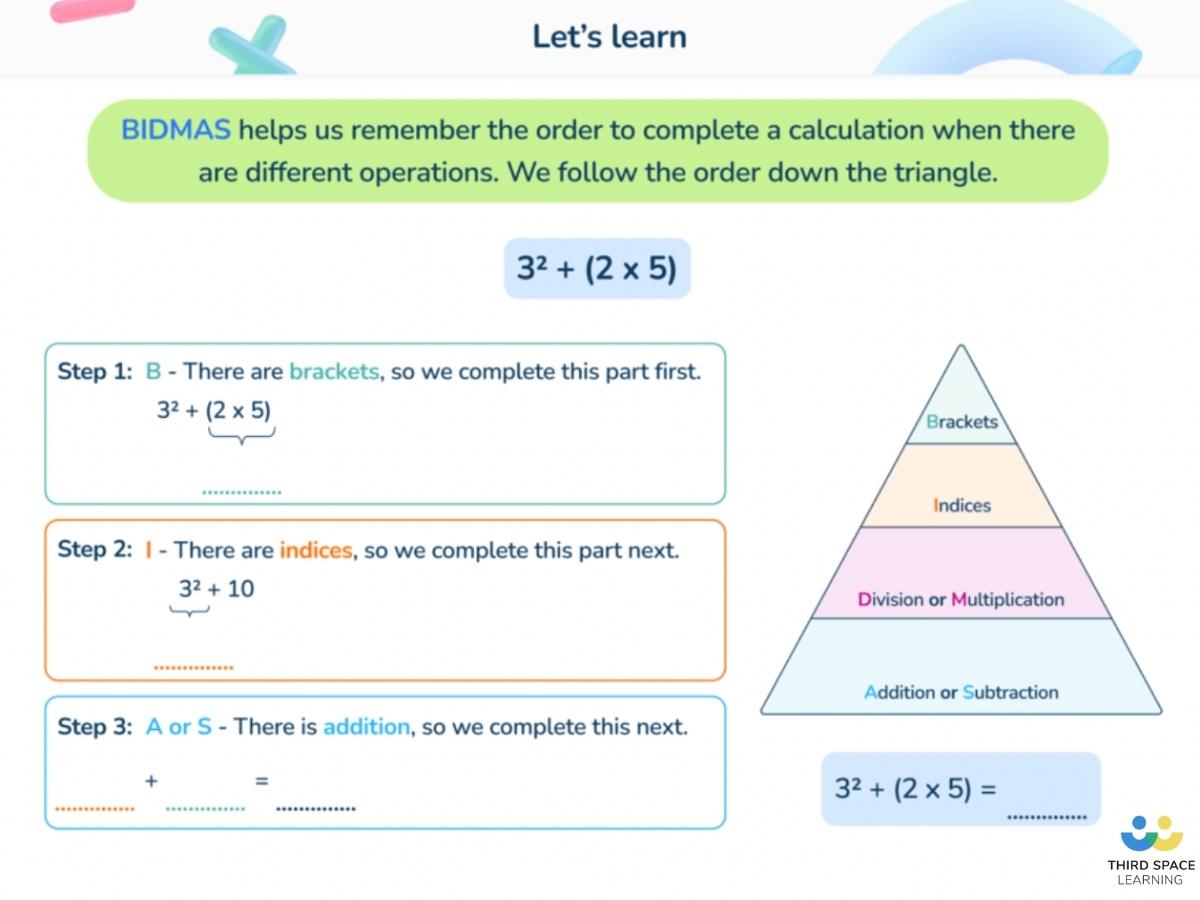
What’s the difference between PEMDAS, BODMAS and BIDMAS?

PEMDAS, BODMAS, and BIDMAS are all acronyms that serve the same purpose – to help students remember the order of operations when solving mathematical equations with multiple operations. These acronyms differ based on where they are used. 

For example, PEMDAS is commonly used by mathematicians in the US, while BODMAS and BIDMAS are commonly used in the UK. Canada and New Zealand often use BEDMAS. The highlighted terms in the table below show where they differ. 

Note that the terms parentheses and brackets, as well as the terms exponents, orders, and indices are referring to the same concepts.

PEMDAS	BODMAS	BIDMAS
Parentheses Exponents Multiplication Division Addition Subtraction	Brackets Orders Division Multiplication Addition Subtraction	Brackets Indices Division Multiplication Addition Subtraction

Why is PEMDAS important?

PEMDAS is important because the order of operations is important! The order of operations is a set of rules for solving math equations and expressions with multiple operations. This set of rules ensures that all math equations are solved in the same way. If equations are solved simply in the order they appear, you may end up with the wrong answer.

Students are able to refer to the rules of PEMDAS to solve equations or evaluate expressions in a correct and consistent step by step process. PEMDAS is important because it provides a way for students to remember this set of rules in the correct order.

How do you remember PEMDAS?

PEMDAS may be memorable for many but some learners may prefer a mnemonic device to help them remember to easily recall each letter of PEMDAS. The most common is Please Excuse My Dear Aunt Sally. 

Some teachers challenge their students to come up with their own mnemonic device for PEMDAS, which may motivate the students to remember the acronym more easily. Students can come up with silly mnemonics, such as Purple Elephants March Down A Street. 

When do children learn about PEMDAS in school?

PEMDAS and the order of operations is most commonly taught in 5th and 6th grade across the country, in schools following the Common Core math and other standards. 

This sets a strong foundation for students to learn more complex mathematical concepts involving algebraic expressions throughout middle school and high school. These more complex equations and expressions may involve square roots, decimals, variables, integers, etc. but the rules of PEMDAS and the order of arithmetic operations will remain consistent.

PEMDAS in 5th grade

PEMDAS and the order of operations first appears in the Common Core Standards in 5th grade under the domain Operations & Algebraic Thinking.

• 5.OA.A.1 Use parentheses, brackets, or braces in numerical expressions, and evaluate expressions with these symbols.
• 5.OA.A.2 Write simple expressions that record calculations with numbers, and interpret numerical expressions without evaluating them. 

Students must be able to evaluate expressions that involve parentheses ( ), brackets [ ], or braces { } and they must understand how to determine in which order they should evaluate each part of the expression. Students may be tempted to move through the expression from left to right, but PEMDAS will help them remember not to do this. 

Students also need to be able to represent mathematical expressions in written form. The wording they use should convey the order in which the parts of the expression should be evaluated. 

For example, we may describe the expression 3 x (5 + 2) as “three times the sum of five and two.” If we described it as “three times five plus two,” this would not convey the fact that the addition (which is within the parentheses) needs to be performed before the multiplication.

PEMDAS in 6th grade

PEMDAS in the 6th grade appears under the domain of Expressions & Equations. Students’ understanding of the order of operations is extended as they work with more complex numerical expressions involving variables, which is a letter used as an unknown number in an expression (i.e., 4 + x = 7). 

Students need to have a strong understanding of the order of operations as they move into this more complex content. Students and teachers will use PEMDAS while tackling these higher-level standards to support their knowledge of the order of operations.

• 6.EE.A.1 Write and evaluate numerical expressions involving whole-number exponents.
• 6.EE.A.2 Write, read, and evaluate expressions in which letters stand for numbers.
• 6.EE.A.3 Apply the properties of operations to generate equivalent expressions. 
• 6.EE.A.4 Identify when two expressions are equivalent.

Note: The standard 6.EE.A.2 has several sub-standards involving numerical expressions which require students’ understanding of the order of operations, as well.

PEMDAS worked examples

PEMDAS worked examples for 5th Grade

Question 1: 6 x 4 + 8 ÷ 2

Step 1: In this example, we see the operations multiplication, addition, and division, in that order. According to PEMDAS, we need to perform any multiplication or division, from left to right as they appear, before any addition or subtraction.

After performing the multiplication, we are left with 24 + 8 ÷ 2

Step 2: Now that we have addition and division left, we perform the division first.

After dividing, we are left with 24 + 4

Answer: 24 + 4 = 28 

Question 2: (8 + 5) – 3 x 2²

Step 1: In this example, we see the operations addition, subtraction, and multiplication, in that order, but we also have a set of parentheses and an exponent. Following PEMDAS, we need to perform anything within parentheses first, then calculate exponents before moving onto the operations.

After calculating inside the parentheses, we are left with 13 – 3 x 2²

Step 2: Now, we move onto the exponent.

After calculating the value of the exponent, we are left with 13 – 3 x 4

Step 3: We have multiplication and subtraction remaining in our expression, so we need to perform the multiplication before the subtraction. Here is where you will most often find students making a mistake. They will want to perform the subtraction first (13 – 3 = 10) and then the multiplication (10 x 4 = 40) but that would give them an incorrect answer of 40.

After performing the multiplication first, we are left with 13 – 12.

Answer: 13 – 12 = 1

Question 3: 5 x [3 + (3² – 8)]

Oftentimes, as 5th graders become more proficient with this content, they will encounter more complex expressions involving more grouping symbols. Instead of just parentheses, they may also see brackets [ ] and braces { }. These should always be performed starting with the innermost grouping symbol, which should be parentheses.

Step 1: We shift our attention to the innermost grouping symbol, the parentheses. Inside the parentheses, we see an exponent as well as subtraction. We need to calculate the value of the exponent first.

After calculating the value of the exponent, we are left with 5 x [3 + (9 – 8)]

Step 2: Now that we have calculated the exponent, we perform the operation within the parentheses, which is subtraction.

After subtracting, we are left with 5 x [3 + 1]

(Notice I have removed the parentheses, since all that was left inside them was a single number.)

Step 3: Now that we have calculated the inside of the parentheses, we move onto the next grouping symbol, which is the brackets. We treat these the same as parentheses, so we need to perform the addition inside them before we can perform the multiplication within our expression.

After performing the addition in the brackets, we are left with 5 x 4

Answer: 5 x 4 = 20

PEMDAS worked examples for 6th Grade

In 6th grade, students use the same concept of PEMDAS and the order of operations, but they have an added layer of complexity as they are introduced to variables, which are letters used in place of unknown numbers.

Question 1: 6 x y² if y = 3

Step 1: The first thing we need to do to find the value of this expression is replace our variable with its value. In this example, we are given the value of our variable y, which is 3.

Once we replace our variable, we are left with 6 x 3²

Step 2: Next, we follow the PEMDAS rule of calculating exponents before any operations. 

Once we evaluate our exponent, we are left with 6 x 9

Answer: 6 x 9 = 54

Question 2:  3n + 8 x (4y – 3) if n = 2 and y = 1

In 6th grade, students are also introduced to a new way to read and write multiplication. As they learn about variables, they also learn that a term such as 3n represents multiplication. The 3 and the variable next to it are meant to be multiplied. Similarly, if students see a number next to a parenthesis, for example 2(4), this also represents multiplication, so this example would equal 8.

Step 1: First, we need to input the values of our variables.

Since n = 2 and y = 1, our expression becomes 3(2) + 8 x (4 x 1 – 3)

Step 2: Now, let’s work within our grouping symbols. The term 4y became 4 x 1, which we know is 4. So we are left with 4 – 3 within our parentheses, which is 1.

3(2) + 8 x (1)

Step 3: Now we are left with multiplication, addition, and multiplication in that order. If there are parentheses left around a single number (1 in this example), it has no significance unless it is directly next to another number, as we see 3(2). As mentioned above, this signifies multiplication.

Let’s perform the multiplication that comes first from left to right to keep in line with our PEMDAS rule. 

We are left with 6 + 8 x (1)

Step 4: Now that we have addition and multiplication remaining, we can perform the other multiplication piece.

We are left with 6 + 8

Answer: 6 + 8 = 14

PEMDAS practice questions

Below, we have included PEMDAS questions suitable for 5th and 6th graders, including answers.

PEMDAS questions for 5th grade:

7 + 3 x 4 ÷ 2

Answer: 13

8 x (12 – 9) + 4 ÷ 2

Answer: 26

6 x 3² + (7 – 4) 

Answer: 57

9 x [18 – (2 x 3)] ÷ 4

Answer: 27

5³  – [3 x (1 + 2)]² 

Answer: 44

PEMDAS questions for 6th grade:

5x – 4² if x = 8

Answer: 24

4(9 – 2²) x 3y if y = 4

Answer: 240

Which exponent makes the equation true?

(9 – 6)³ + _______ = 43 

Answer: 4²

Which number makes the inequality true?

7 + [(4 – 2) x 2]³   >   6 + [(13 – 9) x _____]²

a) 3      b) 2     c) 4    d) 5

Answer: b) 2

Write <, >, or = to make the number sentence true.

3(8 – 3) + 5² ____ 5[2 + 3] + 4²

Answer : <

PEMDAS FAQs