One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
Parts of a circle Angles in polygons Angles on a straight line Angles around a point Angles in parallel lines Triangles PythagorasThis topic is relevant for:

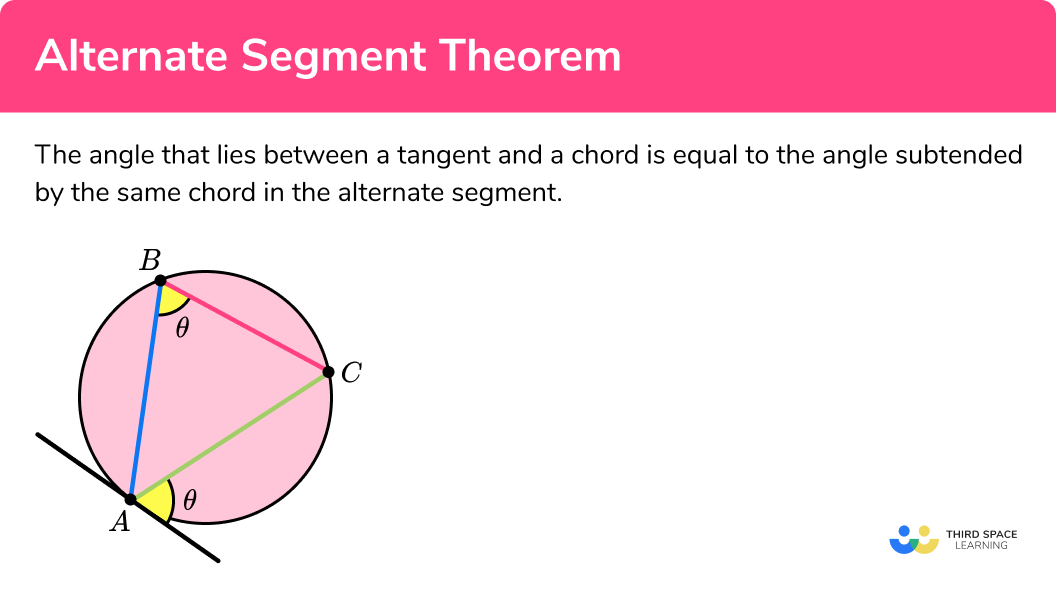
Alternate Segment Theorem
Here we will learn about the alternate segment theorem, including their application, proof, and using them to solve more difficult problems.
There are also circle theorem worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is the alternate segment theorem?
The alternate segment theorem is the angle that lies between a tangent and a chord is equal to the angle subtended by the same chord in the alternate segment.
What is the alternate segment theorem?
Key parts of a circle needed for this theorem
- The circumference of the circle is the distance around the edge of the circle.
- A chord is a straight line that meets the circumference in two places. The longest chord in a circle is the diameter.
- The major segment is the larger part of a circle when it is enclosed by a chord and the major arc.
- The minor segment is the smaller part of a circle when it is cut by a chord and the minor arc.
- The tangent of a circle is a straight line that touches the circumference of the circle with a single point of contact. The tangent is perpendicular ( 90 degrees to) the radius.
Subtended angles
An angle within a circle is created by two chords meeting at a point on the circumference. The diagrams below show the angle subtended by arc AC from point B for two different circles.
Top tip: The word subtend is used a lot within circle theorems so make sure you know what it means.
Proving the alternate segment theorem
To be able to prove the alternate segment theorem, you need to know the following circle theorems:
- The angle at the centre is twice the angle at the circumference.
- Tangents of a circle.
- Chord of a circle.
Step
1
2
3
4
5
6
7
8
Diagram
Description
Let ABC be a triangle within a circle at
centre O. The tangent DE passes
through the point A on the
circumference of the circle only. The line
AB is a chord where the point C lies on
the major arc.
Let us draw the two lines OA and OB.
As they go from the centre to the
circumference of the circle, both the
lines OA and OB are radii
This means that the lines OA and DE
are perpendicular as the tangent to a
circle meets the radius at 90 degrees.
We will come back to this shortly.
As OA and OB are radii, OAB is an
isosceles triangle. This also means that
the angles at A and B are equal. Here
we have labelled them x.
As AB is a chord, the perpendicular
from the centre of a circle to a chord
bisects the chord at 90 degrees. This
creates two right angle triangles that
are congruent (triangle OFA and
triangle OFB are identical).
As triangles OFA and OFB are
congruent, the angles AOF and
BOF are also the same. Here we have
labelled them both y .
Let us now inspect the angles made
with the tangent.
We know that OAE is a 90 degree
angle from Step 2 . As OFA ios a right
angle triangle, x+y=90^o.
This means that angle FAD is also equal to y as if we take away x from
90^o , we get y .
Here we now have the simplified
diagram with the important angles
found. The angle at O is equal to 2y as
originally AOB was made up of y+y ,
which is equal to 2y.
As the angle at the circumference is
twice the angle at the centre, we can
state that the angle at C is equal to y.
So we have angle DAB is equal to
angle ACB.
As AB is the chord, the angle at C is in
the alternate segment to the angle
DAB and so we can state that angles
in the alternate segment are equal.
How to use the alternate segment theorem
In order to use the alternate segment theorem:
- Locate the key parts of the circle for the theorem.
- Use other angle facts to determine one of the two angles.
- Use the alternate segment theorem to state the other missing angle.
Explain how to use the alternate segment theorem


Alternate segment theorem worksheet

Get your free alternate segment theorem worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Alternate segment theorem worksheet

Get your free alternate segment theorem worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated circle theorems
Tangent of a circle is one of 7 circle theorems you will need to know. You may find it helpful to start with our main circle theorems page and then look in detail at the rest.
Alternate segment theorem examples
Example 1: standard diagram
The triangle ABC is inscribed in a circle with centre O. The tangent DE meets the circle at the point A. Calculate the size of the angle ABC.
- Locate the key parts of the circle for the theorem.
Here we have:
- The tangent DE
- The chord AC (that meets the tangent)
- The angle CAE = 56^o
- The angle ABC = \theta
2Use other angle facts to determine one of the two angles.
We already know that CAE = 56^o so we do not need to use any other angle fact to determine this angle for this example.
3Use the alternate segment theorem to state the other missing angle.
ABC = 56^o as angles in the alternate segment are equal to the angle between the tangent and the associated chord.
Example 2: using angles in a triangle
Three chords meet the circumference at the points A, B, and C of the circle with centre O. DE is a tangent that meets the circle at point A. Calculate the size of angle CAE.
Locate the key parts of the circle for the theorem.
Here we have:
- The tangent DE
- The chord AC (that meets the tangent)
- The angle BAC = 68^o
- The angle ACB = 31^o
- The angle CAE = \theta
Use other angle facts to determine one of the two angles.
We can use the alternate segment theorem to find the angle θ if we know the size of angle ABC. As the angle ABC = angle CAE, we can state that angle ABC is equal to \theta :
As ABC is a triangle, we can use the fact that angles in a triangle total 180^o , and so we can find the value of ABC:
\begin{aligned}&ABC=180-(68+31) \\\\ &ABC=81^o \end{aligned}
Use the alternate segment theorem to state the other missing angle.
As ABC = 81^o and angle ABC = angle CAE:
\theta=81^o
Example 3: using another circle theorem (angles in a semicircle)
The triangle ABC is inscribed in a circle with centre O. The tangent DE intersects the circle at the point C. Calculate the size of angle ACD.
Locate the key parts of the circle for the theorem.
Here we have:
- The tangent DE
- The chord AC (that meets the tangent)
- The angle BCA = 17^o
- The angle ACD = \theta
Use other angle facts to determine one of the two angles.
BC is a diameter as it goes through the centre at O. This means that the angle BAC is 90^o as angles in a semicircle are equal to 90^o .
The alternate segment theorem can be used if we know angle ABC as this is equal to angle ACD, which is \theta . Placing this information on the diagram, we now have:
ABC is a triangle and we know two of the three angles so we can now work out the value of angle ABC:
\begin{aligned} &ABC=180-(90+17) \\\\ &ABC=73^o \end{aligned}
Use the alternate segment theorem to state the other missing angle.
As ABC = 73^o and angle ABC = angle ACD:
\theta=73^o
Example 4: using another circle theorem (cyclic quadrilateral)
A, B, C, and D are points on the circumference of the circle with centre O. The line EF is a tangent at C. Calculate the size of the inscribed angle DCF.
Locate the key parts of the circle for the theorem.
Here we have:
- The tangent EF
- The chord CD (that meets the tangent)
- The angle BDC = 72^o
- The angle BAD= 95^o
- The angle DCF = \theta
Use other angle facts to determine one of the two angles.
ABCD is a cyclic quadrilateral and so as opposite angles in a cyclic quadrilateral total 180^o , we can say that angle BCD = 180 - 95 = 85^o . Angle DBC is the required angle \theta in the alternate segment of the chord CD. Here is the updated diagram.
We can calculate angle DBC because BCD is a triangle and angles in a triangle total 180^o . We therefore have
\begin{aligned} &DBC=180-(72+85) \\\\ &DBC=23^o \end{aligned}
Use the alternate segment theorem to state the other missing angle.
As ABC = 23^o and angle DCF and angle DBC are equal angles:
\theta=23^o
Example 5: angles in parallel lines
ABC is a triangle that is inscribed in a circle with centre O. The tangent DE touches the circle at point B and is parallel to the chord AC. Calculate the size of angle ABD.
Locate the key parts of the circle for the theorem.
Here we have:
- The tangent DE
- The chord AB (that meets the tangent)
- The angle ABC= 48^o
- The angle ABD = \theta
Use other angle facts to determine one of the two angles.
As DE and AC are parallel and alternate angles in parallel lines are equal, we can say that angle BAC = \theta . The angle BCA is in the alternate segment to the angle ABD and so this angle is also equal to \theta .
This means that triangle ABC is an isosceles triangle as there are two angles that are equal. Here is the updated diagram showing this information:
Now that we know ABC is isosceles, the size of angle \theta is equal to
\begin{aligned} &\theta=(180-48)\div 2 \\\\ &\theta=66^o \end{aligned}
Use the alternate segment theorem to state the other missing angle.
As angle ABD is equal to angle BCA, we can use the alternate segment theorem to state that angle ABD = 66^o .
Example 6: using another circle theorem (angle at the centre)
A circle has a centre at O and a tangent at the point C. Points A, B, and C lie on the circumference of the circle. OB and OC are radii of the circle. Calculate the size of the angle BCE.
Locate the key parts of the circle for the theorem.
Here we have:
- The tangent DE
- The chord BC (that meets the tangent)
- The angle BOC = 30^o
- The angle BCE = \theta
Use other angle facts to determine one of the two angles.
Angle BAC is in the alternate segment to the angle BCE so if we can calculate the size of this angle, we can then find the size of angle BCE.
As the angle at the centre is twice the angle at the circumference, we can calculate the size of angle BAC.
\begin{aligned} &BAC=30 \div 2\\\\ &BAC=15^o \end{aligned}
Use the alternate segment theorem to state the other missing angle.
As angle BAC is in the alternate segment to the angle BCE, we can use the alternate segment theorem to state that angle BCE = 15^o .
Common misconceptions
- Tangent and radius
As the tangent meets the radius at 90 degrees, the assumption is that the angle in the alternate segment is the remainder of the angle taken from 90^o .
- Parallel lines
Take for example the diagram below:
The chord BC is assumed to be parallel to the tangent and so the angle ABC is equal to the angle at the tangent. Here the angle BCA would be equal.
Top tip: Use arrows to visualise which way the alternate angle appears:
- Opposite angles in a cyclic quadrilateral
The angle is taken from 180^o which is a confusion with opposite angles in a cyclic quadrilateral.
Here, angle ABC is incorrectly calculated as 180 - 56 = 124^o .
The angle ABC = 56^o as it is in the alternate segment to the angle CAE.
- Angle in a semicircle
The angle at the circumference is assumed to be 90 degrees although the associated chord does not go through the centre of the circle.
Practice alternate segment theorem questions
1. A, B, and C are points on the circumference of a circle with centre O. The tangent DE passes through the point A. Calculate the size of angle CAE.




ABC = CAE = 82^o (alternate segment theorem)
2. A, B, and C are points on the circumference of a circle with centre O. The tangent DE passes through the point A. Calculate the size of angle CAE




ABC = 180 \; – \; (74+65) = 41^o
CAE = ABC = 41^o (alternate segment theorem)
3. The points A, B, and C lie on the circle with centre O. The angle BAC = 4^o . DE is a tangent to the circle at point C. Calculate the size of angle BCE.




ABC = 90^o (angles in a semicircle)
BAC = 180\; – \; (90+4) = 86^o
BCE = BAC = 86^o (alternate segment theorem)
4. ABCD is a cyclic quadrilateral. Calculate the size of angle CDF.




ADC = 180 \; – \; 81 = 99^o
ACD = ADF = 55^o (alternate segment theorem)
CDE = 180 \; – \; (99+55) = 26^o (angles on a straight line)
5. A, B, and C are points on the circle with centre O. The chord AB is parallel to the tangent DE where DE passes through the point C. Calculate the size of angle BCE.




ABC is an isosceles triangle as AB is parallel to DE, so AC = BC.
BAC = (180 \; – \; 67) \div 2 = 56.5^o
BCE = BAC = 56.5^o (alternate segment theorem)
6. Below is a circle with centre O. The points A, B, and C lie on the perimeter of the circle with the tangent DE passing through the point A. Angle AOC = 42^o . Calculate the size of angle CAD.




ABC = 24 \times 2 = 84^o
CAD = ABC = 84^o (alternate segment theorem)
Alternate segment theorem GCSE questions
1. The circle with centre O has an inscribed triangle ABC. The tangent DE lies at the point C with angle BAC = 57^o . Calculate the size of angle BCE.
(2 marks)
BCE = 57^o
(1)
The alternate segment theorem
(1)
(a)
CDF = CBD = x = 38^o
(1)
The alternate segment theorem
(1)
(b)
DCB = 180 – (38 + 38) = 104
(1)
DAB = 180 – 104 = 76^o
(1)
(Opposite angles in a cycic quadrilateral add to 180^o )
(1)
ADB = BAH = 180 = 76 – 65 = 39^o
(1)
The alternate segment theorem
(1)
3. Using the information on the diagram below, calculate the size of angle \theta . State all of the assumptions made.
(6 marks)
CED = 180 – 85 = 95^o
(1)
Angles on a straight line total 180^o
(1)
ECD = 180 \; – \;(95 + 25) = 60^o
(1)
Angles in a triangle total 180^o
(1)
ACD = DAF = 60^o
(1)
The angle between the tangent and the chord and the angle in the alternate segment are equal or the alternate segment theorem.
(1)
Learning checklist
You have now learned how to:
- Apply and prove the standard circle theorems concerning angles, radii, tangents and chords, and use them to prove related results
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.