Cyclic quadrilateral

GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

Teacher-trusted tutoring

In order to access this I need to be confident with:

Parts of a circle Angles in polygons Angles on a straight line Angles around a point Angles in parallel lines

Properties of triangles

This topic is relevant for:

GCSE Maths Geometry and Measure Circle Theorems

Cyclic Quadrilateral

Here we will learn about the circle theorem involving cyclic quadrilaterals, including its application, proof, and using it to solve more difficult problems.

There are also circle theorem worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is a cyclic quadrilateral?

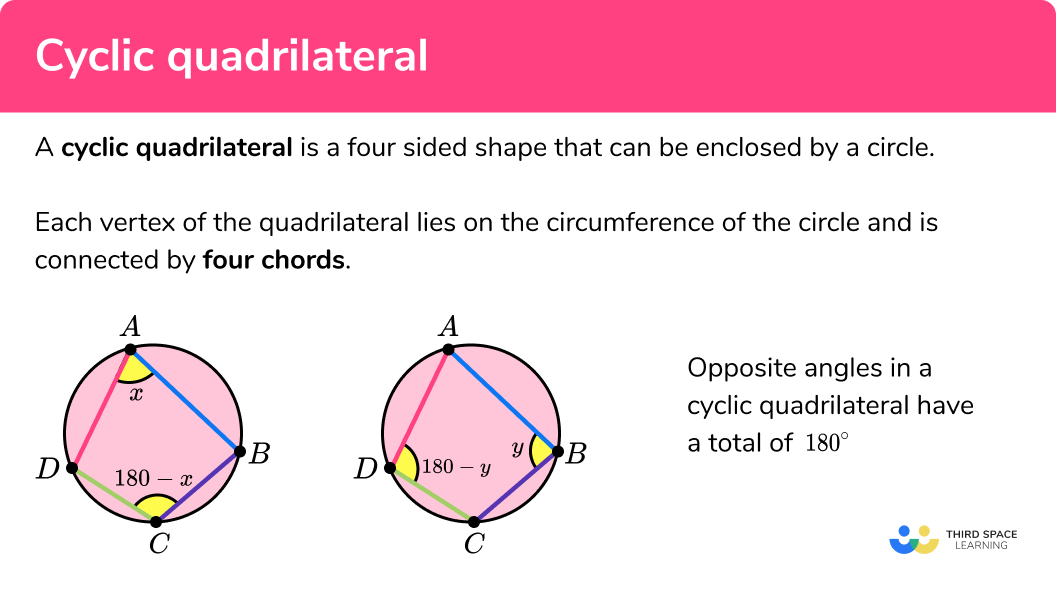
A cyclic quadrilateral is a four sided shape that can be inscribed into a circle. Each vertex of the quadrilateral lies on the circumference of the circle and is connected by four chords.

The opposite angles of a cyclic quadrilateral have a total of $180°.$

In the diagrams above, the points $A, B, C,$ and $D$ are on the circumference of the circle.

The opposite angles of a cyclic quadrilateral have a total of $180°$ and so they are supplementary to one another. This means that the angle at $A$ plus the angle at $C$ is equal to $180°$ , and the angle at $B$ plus the angle at $D$ equal $180°$ .

This also highlights that angles inside a cyclic quadrilateral total $360°$ , which is the same property for any quadrilateral.

What is a cyclic quadrilateral?

Key parts of a circle needed for this theorem

The centre of the circle is a point that locates the middle of a circle (the midpoint of the circle).
The circumference of the circle is the distance around the edge of the circle.
A chord is a straight line that meets the circumference in two places. The longest chord in a circle is the diameter.

Proving that opposite angles of a cyclic quadrilateral total 180°

To be able to prove that opposite angles of a cyclic quadrilateral total $180°$ , you need to know the following circle theorems:

The angle at the centre is twice the angle at the circumference

Step	Diagram	Description
1		ABCD is a quadrilateral inscribed by a circle with centre O.
2		By drawing two radii from OB and OD, we can split the quadrilateral into two smaller quadrilaterals that tessellate around the centre of the circle.
3		If the angle A is labelled a, the angle BOD is equal to 2a as the angle at the centre is twice the angle at the circumference.
4		If the angle at C is labelled c, the other angle at BOD is equal to 2c for the same reason as in Step 3.
5		This means that we have the point at the centre with the angles 2a and 2c.
	Angles around a point total 360°	Therefore, we can state that 2 a + 2 c = 360 Or by simplifying it (dividing throughout by 2): a + c = 180° This means that opposite angles of a cyclic quadrilateral total 180°.

How to use the cyclic quadrilateral theorem

In order to use the cyclic quadrilateral theorem:

Locate the key parts of the circle for the theorem.
Use other angle facts to determine one of the two opposing angles in the quadrilateral.
Use the cyclic quadrilateral theorem to state the other missing angle.

How to use the cyclic quadrilateral theorem

Cyclic quadrilateral worksheet

Get your free cyclic quadrilaterals worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Cyclic quadrilateral worksheet

Get your free cyclic quadrilaterals worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Tangent of a circle is one of 7 circle theorems you will need to know. You may find it helpful to start with our main circle theorems page and then look in detail at the rest.

Cyclic quadrilateral examples

Example 1: standard diagram

$ABCD$ is a cyclic quadrilateral. Calculate the size of angle $BCD$ :

Locate the key parts of the circle for the theorem.

Here we have:

The angle $BAD = 51°$
The angle $BCD = θ$

2Use other angle facts to determine one of the two opposing angles in the quadrilateral.

We already know that $BAD = 51°$ so we do not need to use any other angle fact to determine this angle for this example.

3Use the cyclic quadrilateral theorem to state the other missing angle.

As opposite angles of a cyclic quadrilateral total $180°$ , we can calculate the size of angle $BCD$ :

\[BCD=180-51\\ BCD=129^{\circ}\]

Example 2: unnecessary information

$ABCD$ is a cyclic quadrilateral. Calculate the size of angle $BAD$ :

Locate the key parts of the circle for the theorem.

Here we have:

The angle $BCD = 105°$
The angle $ABC = 138°$
The angle $BAD = θ$

Use other angle facts to determine one of the two opposing angles in the quadrilateral.

We already know that $BCD = 105°$ so we do not need to use any other angle fact to determine this angle for this example.

Top tip: sometimes you are given extra information that you need to filter through in order to use what you need, rather than using everything you have been given. It is important to know what information is important, and what is irrelevant.

Use the cyclic quadrilateral theorem to state the other missing angle.

As opposite angles of a cyclic quadrilateral total $180°$ , we can calculate the size of angle $BAD$ :

\[BAD=180-105\\ BCD=75^{\circ}\]

Example 3: angles in a semicircle

$ABCD$ is a cyclic quadrilateral with center $O$ . Calculate the size of angle $ABC$ .

Locate the key parts of the circle for the theorem.

Here we have:

The angle $ADB = 35°$
The angle $BDC = 64°$
The angle $BCD$ = angle $BAD = 90°$
The angle $ABC = θ$

Use other angle facts to determine one of the two opposing angles in the quadrilateral.

We already know angle $BDA$ and angle $CDB$ and so together they are opposite the angle $ABC$ . This means that we can calculate $ADC$ :

\[ADC=64+35\\ ADC=99^{\circ}\]

Use the cyclic quadrilateral theorem to state the other missing angle.

As opposite angles of a cyclic quadrilateral total $180°$ , we can calculate the size of angle $ABC$ :

\[ABC=180-99\\ ABC=81^{\circ}\]

Example 4: isosceles triangles

$ABCD$ is a cyclic quadrilateral inside a circle with centre $O$ . $BOC$ is the inscribed angle of the chord $BC$ . Calculate the size of angle $ADC$ .

Locate the key parts of the circle for the theorem.

Here we have:

The angle $ABO = 48°$
The angle $BOC = 100°$
The angle $ADC = θ$

Use other angle facts to determine one of the two opposing angles in the quadrilateral.

$OBC$ is an isosceles triangle because $OB$ and $OC$ are radii of the circle. This means that the other two angles in the triangle are the same size, so angle $OBC$ can be calculated:

\[OBC=(180-100)\div2\\ OBC=40^{\circ}\]

As angle $OBC=40°$ , we can now calculate angle $ABC$ , which is the angle opposite angle $ADC$ .

\[ABC=48+40\\ ABC=88^{\circ}\]

Use the cyclic quadrilateral theorem to state the other missing angle.

As opposite angles of a cyclic quadrilateral total $180°$ , we can calculate the size of angle $ADC$ :

\[ADC=180-88\\ ADC=92^{\circ}\]

Example 5: angles in triangles

The circle below contains the quadrilateral $ABCD$ . Calculate the size of angle $CAD$ :

Locate the key parts of the circle for the theorem.

Here we have:

The angle $BDC = 36°$
The angle $CBD = 58°$
The angle $AEB = 119°$
The angle $CAD = θ$

Use other angle facts to determine one of the two opposing angles in the quadrilateral.

We need to determine the size of angle $BCD$ in order to find the size of angle θ. Using angle $AEB$ , we can determine all the angles around the point. Angles on a straight line total $180°$ and so angle $BEC = AED = 180 - 119 = 61°$ . Vertically opposite angles are equal so angle $CED = 119°$

We can now calculate angle $BCD$ by finding angles $BCE$ and $DCE$ using angles in triangles total $180°$ .

\[BCE=180-(58+61)\\ BCE=61^{\circ}\]

\[DCE=180-(119+36)\\ DCE=25^{\circ}\]

Finally we can calculate the size of the angle $CAB$ . This is because angles in the same segment are equal and so angle $CAB$ = angle $BDC$ . $CAB = 36°$ .

Use the cyclic quadrilateral theorem to state the other missing angle.

As opposite angles of a cyclic quadrilateral total $180°$ , we can calculate the size of angle $BAD$ :

\[BAD=180-(25+61)\\ BAD=94^{\circ}\]

As we know that angle $BAD = 94°$ and angle angle $BAC = 36°$ , we can finally calculate the size of angle $CAD$ :

\[CAD=94-36\\ CAD=58^{\circ}\]

Example 6: tangents to a circle

$ABCD$ are vertices of the quadrilateral inscribed in a circle with centre $E$ . $BF$ and $CF$ are tangents to the circle with centre $E$ . Calculate the size of angle $CDE$ .

Locate the key parts of the circle for the theorem.

Here we have:

The angle $BEC = 90°$
The angle $CDE = θ$
$BF$ and $CF$ are tangents
$AC$ and $BD$ are diameters

Use other angle facts to determine one of the two opposing angles in the quadrilateral.

As $AC$ and $BD$ are perpendicular bisectors, $BE$ and $CE$ are radii that meet at $90°$ .

$EBF$ and $ECF$ are $90°$ angles because the angle between the tangent and the radius is $90°$ . Tangents that meet at the same point are equal length and so $BE$ and $CF$ must be parallel and $CE$ and $BF$ are also parallel. All the sides are the same length, and meet at a right angle.

As opposite sides of the quadrilateral are equal and perpendicular to each other, $BECF$ is a square.

As $AC$ is a diameter, angles in a semicircle equal $90°$ so angle $ABC = 90°$ .

Use the cyclic quadrilateral theorem to state the other missing angle.

As opposite angles of a cyclic quadrilateral total $180°$ , we can calculate the size of angle $ADC$ :

\[ADC=180-90\\ ADC=90^{\circ}\]

$AC$ and $BD$ are perpendicular and they are both diameters. The intersection of the diagonals of the quadrilateral are at right angles to each other, so $ABCD$ is a square. This means that the line $BD$ is a diagonal, which bisects the angle $ADC$ . This means that we can calculate the size of angle $CDE$ :

\[CDE=90\div2\\ CDE=45^{\circ}\]

Common misconceptions

Angle at the centre is supplementary to opposing angle

As the shape is a quadrilateral, the angle at the centre is assumed to be supplementary and add to $180°$ .

Opposite angles are the same

As angles in the same segment are equal, the opposing angles in a quadrilateral are assumed to be equal. The only case of this is when both angles are $90°$ . As angles in the same segment are equal, the opposing angles in a quadrilateral are assumed to be equal. The only case of this is when both angles are $90°$ .

Opposite angles are double

Similar to the angle at the centre theorem, it is assumed that the opposing angle in a cyclic quadrilateral is double or half of the other.

Opposite angles don’t add up to $180°$

The angles in a cyclic quadrilateral are calculated incorrectly (usually after forming and solving an equation and so the opposite angles do not add to $180°$ .

Practice cyclic quadrilateral questions

117^{\circ}

63^{\circ}

126^{\circ}

127^{\circ}

$180-63=117^{\circ}$ (opposite angles of a cyclic quadrilateral total $180^{\circ}$ )

85^{\circ}

95^{\circ}

170^{\circ}

94^{\circ}

$180-85=95^{\circ}$ (opposite angles of a cyclic quadrilateral total $180^{\circ}$ )

46^{\circ}

73^{\circ}

61^{\circ}

12^{\circ}

$180-107=73^{\circ}$ (opposite angles of a cyclic quadrilateral total $180^{\circ}$ )
$73-61=12^{\circ}$

122^{\circ}

148^{\circ}

61^{\circ}

119^{\circ}

$360-122=238^{\circ}$ (angles around a point total $360^{\circ}$ )
$238\div2=119^{\circ}$

39^{\circ}

57^{\circ}

92^{\circ}

123^{\circ}

$180-(18+39)=123^{\circ}$ (opposite angles of a cyclic quadrilateral total $180^{\circ}$ )
$ACB = 31^{\circ}$ as angles in the same segment are equal.
$123-31=92^{\circ}$

43^{\circ}

55^{\circ}

78^{\circ}

36^{\circ}

$ODF = 90^{\circ}$ so $OCD = 90-43 = 47^{\circ}$ (tangent and radius meet at $90^{\circ}$ )
$BOD=78\times2=156^{\circ}$ (angle at the centre is twice the angle at the circumference)
$BCD=180-78=102^{\circ}$ (opposite angles of a cyclic quadrilateral total $180^{\circ}$ )
$OBC=360-(47+156+102)=55^{\circ}$ (angles in a quadrilateral total $360^{\circ}$ )

Cyclic quadrilateral GCSE questions

1. $PQRS$ is a quadrilateral inscribed in a circle. Calculate the value of $x$ .

(3 marks)

Show answer

$180 – 124 = 56^{\circ}$

(1)

$4x=56^{\circ}$

(1)

$x=14^{\circ}$

(1)

2. Below is a semicircle:

(a) Malik says “the angle = $90^{\circ}$ because the angle in a semicircle is equal to $90$ degrees”. Explain why Malik is not correct.

(b) Calculate the size of angle $\theta$ . Justify your answer.

(3 marks)

Show answer

(a)

The angle in a semicircle is equal to $90^{\circ}$ when the angle is subtended from the chord $A$ and $B$ .

The angle $BCD$ is subtended from the chord $BD$ and so it does not equal $90^{\circ}$ as $BD$ is not the diameter of the semicircle.

(1)

(b)

$180 – 52 = 128^{\circ}$

(1)

Opposite angles in a cyclic quadrilateral total $180^{\circ}$

(1)

3. (a) $ABCD$ is an inscribed quadrilateral within a circle. $AC$ and $BD$ intersect at the point $E$ . Use the information given to calculate $x$ , the angle $DCE$ .

(b) Hence calculate the value of $y$ . Justify your answer.

(9 marks)

Show answer

(a)

$ADB = 7^{\circ}$

(1)

Angles in the same segment are equal

(1)

$CDE = 87 – 7 = 80^{\circ}$

(1)

$CED = 44^{\circ}$

(1)

Vertically opposite angles are equal

(1)

$DCE = 180 – (80+44) = 56^{\circ}$

(1)

Angles in a triangle total $180^{\circ}$

(1)

(b)

$180 – (56+7) = 117^{\circ}$

(1)

Opposite angles in a cyclic quadrilateral total $180^{\circ}$

(1)

Learning checklist

You have now learned how to:

Apply and prove the standard circle theorems concerning angles, radii, tangents and chords, and use them to prove related results

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.