One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

Learn more

In order to access this I need to be confident with:

Parts of a circle Angles in polygons Angles on a straight line

This topic is relevant for:

GCSE Maths Geometry and Measure Circle Theorems

Subtended

Subtended Angles

Here we will learn about subtended angles, including subtended angles of a line, curve and within polygons.

There are also subtended angles worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is a subtended angle?

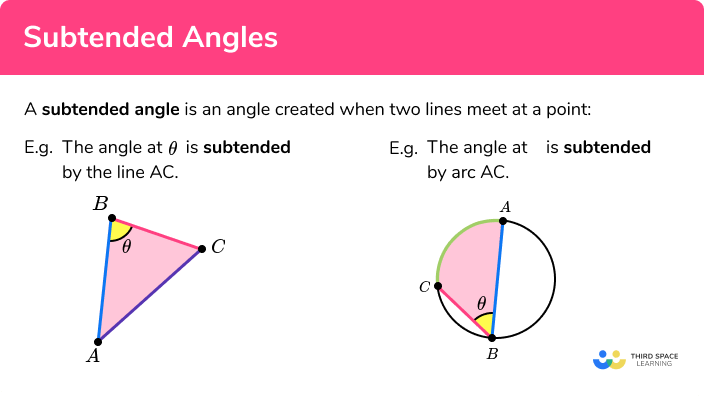
A subtended angle is the angle between two lines at a point.

For example,

The side $AC$ subtends the angle θ from point $B$ .

We can, therefore, describe a subtended angle as the angle made from a given point.

For circle theorems, a subtended angle is an angle within a circle that is created by two chords meeting at a point on the circumference of a circle.

The diagrams below show the angle subtended by arc $AC$ from point $B$ for two different circles.

What is a subtended angle

Important notation

How to find subtended angles

In order to find subtended angles:

Use angle facts to determine missing angles.
Use the appropriate circle theorem to find the subtended angle.

How to find subtended angles

Circle theorems worksheet (including subtended angles)

Get your free circle theorems worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Circle theorems worksheet (including subtended angles)

Get your free circle theorems worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Tangent of a circle is one of 7 circle theorems you will need to know. You may find it helpful to start with our main circle theorems page and then look in detail at the rest.

Subtended angles examples

Example 1: angles in the same segment

In the diagram, $∠BAC=70°$ , $∠ACB=40°$ . Find $∠ADC$ .

Use angle facts to determine missing angles.

As angles in a triangle total $180°$ , angle $ABC = 180 - (70+40) = 70°$ .

2Use the appropriate circle theorem to find the subtended angle.

As angles in the same segment are equal and $AC$ is a chord shared by the points $B$ and $D$ within the same segment, the angle $ADC$ = angle $ABC = 70°$ .

Example 2: angles in the same segment

The diagram shows a circle with centre $D$ and $∠CAD=42°$ . Find $∠ABC$ .

Use angle facts to determine missing angles

Triangle $ACD$ is isosceles as $AD$ and $AC$ are radii. This means that angle $ADC = 180 - (42 + 42) = 96°$ .

Use the appropriate circle theorem to find the subtended angle.

The angle at the centre is twice the angle at the circumference and so as the angles $ABC$ and $ADC$ are subtended by the same arc $AC$ , angle $ABC$ is half of angle $ADC$ :

$ABC = 96 \div 2 = 48°$ .

Example 3: angles in a semicircle

The diagram shows a circle with centre $C$ and $∠ABD=27°$ . Find $∠CAD$ .

Use angle facts to determine missing angles.

Triangle $ABC$ is isosceles as $AC$ and $BC$ are radii. Angle $BAC = 27°$ .

Use the appropriate circle theorem to find the subtended angle.

The angle at the circumference of a semicircle is equal to $90$ degrees as the line $BD$ is the diameter. This means that angle $CAD = 90 - 27 = 63°$ .

Example 4: cyclic quadrilateral

In the diagram, $∠CBD=43°$ and $∠CDB=22°$ . Find $∠BAD$ .

Use angle facts to determine missing angles.

As angles in a triangle total $180°$ , angle $BCD = 180 - (22+43) = 115°$ .

Use the appropriate circle theorem to find the subtended angle.

Opposite angles in a cyclic quadrilateral total $180°$ .

So, angle $BAD = 180 - 115 = 65°$ .

Example 5: alternate segment theorem

In the diagram, $O$ is the centre, $∠ACB=58°$ and $AD$ and $BC$ are parallel. Find $∠CDF$ .

Use angle facts to determine missing angles.

As lines $AD$ and $BC$ are parallel, we can state that angle $CAD$ is alternate to angle $BCA$ and so angle $CAD = 58°$ .

Use the appropriate circle theorem to find the subtended angle

The angle at $A$ is subtended by the chord $CD$ . The angle $CDF$ is in the alternate segment to angle $CAD$ so angle $CDF = 58°$ .

Example 6: angles in the same segment

In the diagram, $∠ABD=80°$ and $∠ADE=23°$ . Find $∠DCE$ .

Use angle facts to determine missing angles.

For this problem, we need to use circle theorems to state missing angles.

Angle $BAD$ = Angle $BED = 90°$ as angles in a semicircle are $90°$ . This means that angle $BDA = 180 - (90 + 80) = 10°$ .

This means that $BDE = 33°$ and so $DBE = 180 - (90+33) = 57°$ .

Use the appropriate circle theorem to find the subtended angle.

The angles at $B$ and $C$ are subtended by the chord $DE$ . This means that they are in the same segment and so $DCE = 57°$ .

Common misconceptions

Add to $\pmb{90/180/360}$ degrees
Make sure you know the other angle facts including:
- Angles on a straight line total $180°.$
- Angles at a point total $360°.$
- Angles in a triangle total $180°.$
- Angles in a quadrilateral total $360°.$

Halving and doubling
By remembering the angle at the centre theorem incorrectly, the student could double the angle at the centre, or half the angle at the circumference.
Top tip: look at the angles. The angle at the centre is always larger than the angle at the circumference (this isn’t so obvious when the angle at the circumference is in the opposite segment).

Angles are the same
Make sure that you know when two angles are equal. Look out for isosceles triangles and the angles in the same segment.

A diameter or a chord?
The angle at the circumference is assumed to be $90°$ when the associated chord does not intersect the centre of the circle and so the diagram does not show a semicircle.

Practice subtended angles questions

83^{\circ}

41^{\circ}

56^{\circ}

82^{\circ}

$ADB = 180 – (83+41) = 56^{\circ}$ (Angles in a triangle total $180^{\circ}$

Angle $ADC$ = Angle $ACB$ (Angles in the same segment are equal)

ACB = 56^{\circ}

38^{\circ}

52^{\circ}

76^{\circ}

104^{\circ}

$ADC = 38\times2 = 76^{\circ}$ (the angle at the centre is twice the angle at the circumference)

Triangle $ACD$ is isosceles so angle $ACD = (180 – 76)\div2 = 52^{\circ}$

26.5^{\circ}

37^{\circ}

53^{\circ}

90^{\circ}

$BE$ is a diameter

BAE = 90^{\circ}

29^{\circ}

53^{\circ}

39^{\circ}

44^{\circ}

$BAD = 180 – 88 = 92^{\circ}$ (opposite angles in a cyclic quadrilateral total $180^{\circ}$ )

$DAE = 180 – (78+49) = 53^{\circ}$ (angles in a triangle total $180^{\circ}$ )

BAE = 92 – 53 = 29^{\circ}

29^{\circ}

32^{\circ}

58^{\circ}

116^{\circ}

Angle $ACB$ $= 58^{\circ}$ (Angle $ACB$ is in the alternate segment to angle $ABE$ )

Angle $AOB = 58\times2 = 116^{\circ}$ (angle at the centre is twice the angle at the circumference)

55.5^{\circ}

132^{\circ}

120^{\circ}

69^{\circ}

Angle $ADC = 90^{\circ}$ and $ACD$ is an isosceles triangle so
angle $ACD = 45^{\circ}$

Angle $BCO = 111-45 = 66^{\circ}$

Angle $AOB = 66\times2 = 132^{\circ}$ (angle at the centre is twice the angle at the circumference)

Subtended angles GCSE questions

1. Triangle $ABC$ is inscribed inside a circle with centre $O$ . $AB = AC = 5cm$ and $BC = 6cm$ . Calculate the size of the angle subtended at $A$ from the chord $BC$ .

(3 marks)

Show answer

$\theta=\cos^{-1}\left(\frac{b^2+c^2-a^2}{2bc}\right)$

(1)

$\theta=\cos^{-1}\left(\frac{7}{25}\right)$

(1)

$\theta=73.7^{\circ}$

(1)

2. The points $A, B, C,$ and $D$ are points on the circumference of the circle. Lines $AC$ and $BD$ intersect at the point $E$ . Calculate the size of angle $CBD$ .

(4 marks)

Show answer

$CAD = 180 – (68+35) = 77^{\circ}$

(1)

Angles in a triangle total $180^{\circ}$

(1)

$CBD = CAD = 77^{\circ}$

(1)

Angles at $A$ and $B$ are subtended by the same chord $CD$ and so they are equal

(1)

3. In the diagram, angle $DAC = 30^{\circ}$ . The angle at $D$ and the angle at $B$ are subtended by the chord $AC$ . Calculate the size of angle $ABC$ .

(4 marks)

Show answer

$DAC$ is an isosceles triangle

(1)

$ADC = 180 – (30+30) = 120^{\circ}$

(1)

$ABC = 120\div 2 = 60^{\circ}$

(1)

Angle at the centre is twice the angle at the circumference

(1)

Learning checklist

You have now learned how to:

Apply and prove the standard circle theorems concerning angles, radii, tangents and chords, and use them to prove related results

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.