Chord of a circle

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

Learn more

In order to access this I need to be confident with:

Parts of a circle Angle rules Circle theorems Triangles Pythagoras theorem Trigonometry

This topic is relevant for:

GCSE Maths Geometry and Measure Circle Theorems

Chord Of A Circle

Here we will learn about circle theorems involving chords of a circle, including its application, proof, and using it to solve more difficult problems.

There are also circle theorem worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is the chord of a circle?

The chord of a circle is a straight line that connects two points on the circumference of a circle. The longest chord in a circle is the diameter of the circle.

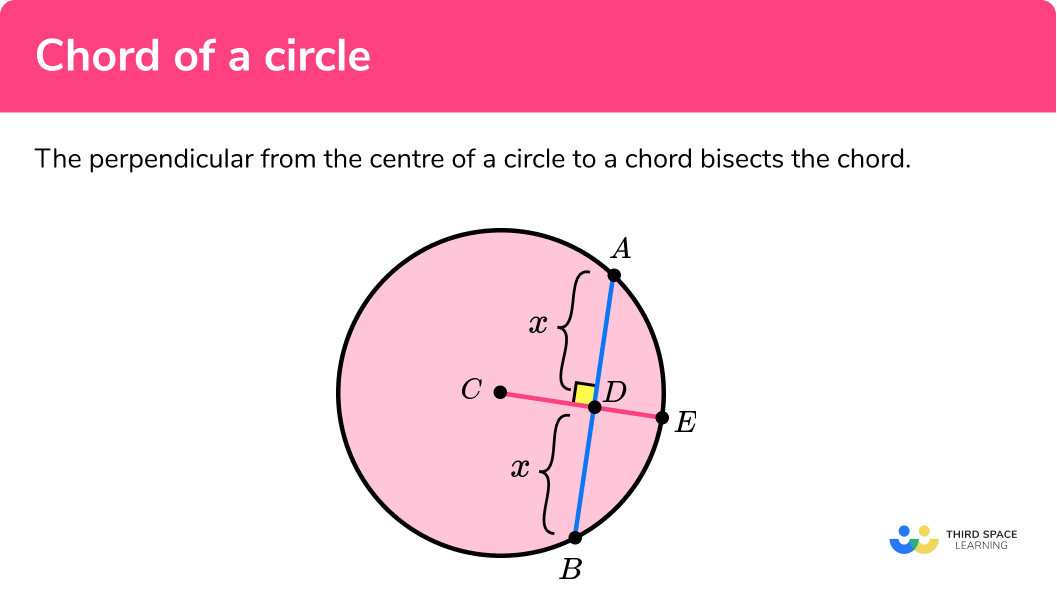
The perpendicular from the centre of a circle to a chord bisects the chord (splits the chord into two equal parts).

In the diagram above, $AB$ is a chord and $CE$ is a radius. Here we can see that the radius $CE$ bisects the chord $AB$ at $90$ degrees and the lengths $AD = BD = x$ .

What is the chord of a circle?

Key parts of a circle

Below is a diagram showing the key parts of a circle for this theorem:

The diameter of the circle is the width of a circle, through the centre. The endpoints of the diameter lie on the circumference of the circle. The diameter is twice the length of the radius of the circle.
An arc is a part of the circumference.
The major segment is the larger part of a circle when it is enclosed by a chord and the major arc.
The minor segment is the smaller part of a circle when it is cut by a chord and the minor arc.
The radius of a circle is the distance between the centre of the circle and the circumference of the circle.

Subtended angles

An angle within a circle is created by two chords meeting at a point on the circumference. The diagrams below show the inscribed angle subtended by arc $AC$ from point $B$ for two different circles.

Top tip: The word subtend is used a lot within circle theorems so make sure you know what it means.

Proving that the perpendicular bisector from the centre of a circle to a chord bisects the chord

To be able to prove this theorem, you do not need to know any other circle theorem. You just need to be confident with angles in a triangle and congruence.

Step	Diagrams	Description
1		Let’s start with the circle with centre C. The line AB is a chord and CE is a radius. The lines CE and AB intersect at the point D at 90 degrees to one another because they are perpendicular.
2		We then draw the lines AC and BC. The length AC = BC as they are both radii of the circle. Triangles ACD and BCD are therefore both right angles, their hypotenuse are equal and the line CD is the same as it is shared between both triangles. This means that the triangles are congruent and so the line segment BD and the line segment AD are the same length or BD = AD.

How to find missing lengths using chords

In order to find missing angles or the length of a chord:

Locate the key parts of the circle for an appropriate circle theorem.
Use other angle facts to determine any missing angles.
Use Pythagoras’ Theorem or Trigonometry to find the missing length.

How to find missing lengths using chords

Chord of a circle worksheet

Get your free Chord of a circle worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Chord of a circle worksheet

Get your free Chord of a circle worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Tangent of a circle is one of 7 circle theorems you will need to know. You may find it helpful to start with our main circle theorems page and then look in detail at the rest.

Chord of a circle examples

Example 1: cosine ratio

Below is a circle with centre $C$ . Points $A, B, C,$ and $D$ are on the circumference of the circle. The chord $AB$ is perpendicular to the line $CD$ at the point $E$ . The line $AE$ is $5cm$ and angle $ADE = 71°$ . Calculate the length of the line $BC$ correct to $1$ decimal place.

Locate the key parts of the circle for an appropriate circle theorem.

Here we have:

$CD$ is a diameter
$AB$ is a chord, perpendicular to $CD$
The angle $ADE = 71°$
The angle $BEC = 90°$
The line $AE = 5cm$
The line $BC = x$

2Use other angle facts to determine other necessary angles.

As angles in the same segment are equal, angle $ADE$ is equal to angle $ABC$ so angle $ABC = 71°$ . Also, as the perpendicular from the centre of a circle to a chord bisects the chord, the line $BE$ is equal to $AE$ , so $BE = 5cm$ .

3Use Pythagoras’ theorem or trigonometry to find the missing length.

To calculate the length of the chord $BC$ , we need to use trigonometry as we know one side length and two angles where one angle is $90°$ .

As we know the side adjacent to the angle and we want to calculate the hypotenuse, we need to use $\cos(\theta)=\frac{A}{H}$ with $H$ as the subject.

$H=\frac{A}{\cos(\theta)}$

$x=\frac{5}{\cos(71)}$

$x=15.4cm (1dp)$

Example 2: sine ratio

Below is a circle with centre $O$ . $A, B, C,$ and $D$ lie on the circumference. $AC$ and $BD$ are perpendicular lines. Calculate the length of $AE$ , correct to $1$ decimal place.

Locate the key parts of the circle for an appropriate circle theorem.

Here we have:

$BD$ is a diameter
$AC$ is a chord, perpendicular to $BD$
The angle $CDE = 35°$
The angle $CED = 90°$
The line $CD = 8cm$
The line $AE = x$

Use other angle facts to determine other necessary angles.

As the perpendicular from the centre of a circle to a chord bisects the chord this means that the length $AE$ is the same as the length $CE$ .

Use Pythagoras’ theorem or trigonometry to find the missing length.

We can calculate the length of $CE$ using the right angle triangle $DEC$ as we know the hypotenuse, an angle and we are finding a missing side:

\[CE=Hsin\times(\theta)\\ CE=8\times\sin(35)\\ CE=4.6cm (1dp)\]

Example 3: tangent ratio

Below is a circle with centre $O$ . $A, B, C,$ and $D$ lie on the circumference. $AC$ and $BD$ are perpendicular lines. $FG$ is a tangent at the point $B$ and is parallel to the line $AC$ . Calculate the length of $BE$ , correct to $1$ decimal place.

Locate the key parts of the circle for an appropriate circle theorem.

Here we have:

$BD$ is a diameter
$AC$ is a chord, perpendicular to $BD$
The angle $ABF = 77°$
The line $CE = 12cm$
The line $BE = x$

Use other angle facts to determine other necessary angles.

As the perpendicular from the centre of a circle to a chord bisects the chord this means that the length $AE$ is the same as the length $CE$ .

As the tangent and the radius meet at $90°$ , the angle $EBF = 90°$ . This means that we can calculate the angle $ABE$ :

\[ABE=90-77\\ ABE=13^{\circ}\]

Use Pythagoras’ theorem or trigonometry to find the missing length.

We can calculate the length of the chord $BE$ using the right angle triangle $ABE$ as we know the opposite side to the angle $ABE$ , the angle $ABE$ and we are finding a missing adjacent side $BE$ :

$BE=\frac{O}{\tan(\theta)}$

$x=\frac{12}{\tan(13)}$

$x=52.0cm (1dp)$

Example 4: Pythagoras theorem

$A, B, C,$ and $D$ are points on the circle with centre $O$ . The radius $OA = 6cm$ and the chord $AB = 13cm$ . The chord $BD$ is perpendicular to the diameter $AC$ at $E$ .

$OE:OC = 1:1$ . Calculate the length of $BE$ marked $x$ .

Locate the key parts of the circle for an appropriate circle theorem.

Here we have:

$AC$ is a diameter
$BD$ is a chord, perpendicular to $AC$
The line $AB = 13cm$
The line $OA = 6cm$
The line $BE = x$

Use other angle facts to determine other necessary angles.

$AEB$ is equal to $90°$ as the chord is perpendicular to the diameter. As $OE:OC = 1:1$ , the line segments $OE$ and $OC$ are equidistant so $OE$ is half of the radius and so $OE = 3cm$ . This means that $AE = 6 + 3 = 9cm$ . We now have

Use Pythagoras’ theorem or trigonometry to find the missing length.

We have a right angle triangle $ABE$ and as the missing length can be found using the other two sides of the triangle, we will use Pythagoras’ Theorem:

\[x^2=13^2-9^2\\ x^2=169-81\\ x^2=88\\ x=9.38cm (2dp)\]

Example 5: isosceles triangle

A circle with centre $O$ has the perpendicular diameters $AC$ and $BD$ . Use the information in the diagram to calculate the value of $x$ .

Locate the key parts of the circle for an appropriate circle theorem.

Here we have:

$AC = BD$ is a diameter
$AC$ and $BD$ are perpendicular
The line $OC = 4cm$
The line $AB = x$

Use other angle facts to determine other necessary angles.

$OA = OB = OC = OD$ are all radii and so we can state $OA = OB = 4cm$ . $AOB$ is equal to $90°$ as $AC$ and $BD$ are perpendicular.

Use Pythagoras’ theorem or trigonometry to find the missing length.

As we know two sides of the right angle triangle $AOB$ , we need to use Pythagoras’ Theorem to find the value of $x$ (the length of the chord $AB$ ).

\[x^2=4^2+4^2\\ x^2=16+16\\ x^2=32\\ x=4\sqrt{2}cm\]

Example 6: semicircle

The diagram below shows a semicircle. The line $BF$ is a chord that is perpendicular to the diameter. Calculate the length of the diameter $AD$ .

Locate the key parts of the circle for an appropriate circle theorem.

Here we have:

$AD$ is a diameter
$BF$ is a chord, perpendicular to $AD$
The angle $BGE = 112°$
The line $DE = 3cm$
The line $AD = x$

Use other angle facts to determine other necessary angles.

The angle in a semicircle is equal to $90°$ so angle $AEB = 90°$ . Angles on a straight line total $180°$ , so $BGA = 180 - 112 = 68°$ . As angle $ABG = 90°$ , angle $BAG = 180 - (90 + 68) = 22°$ . We now know

Use Pythagoras theorem or trigonometry to find the missing length.

As ADE is a right angle triangle with $DE = 3cm$ and $DAE = 22°$ , we can use trigonometry to calculate the side $AD$ :

\[H=\frac{Opp}{\sin(\theta)}\\ H=\frac{3}{\sin(22)}\\ H=8.0cm (1dp)\]

Common misconceptions

Pythagoras’ theorem missing side

The missing side is calculated by incorrectly adding the square of the hypotenuse and a shorter side, or subtracting the square of the shorter sides.

Incorrect trigonometric function

The incorrect trigonometric function is used and so the side or angle being calculated is incorrect. This also includes the inverse trigonometric functions.

Incorrect assumption of isosceles triangles

The intersection of the diameter and the chord at $90$ degrees can be very close to the centre and so the two lengths coming from the point of intersection to the radius are assumed to be equal, but they aren’t.

Practice chord of a circle questions

4cm

2\sqrt{3}

\frac{\sqrt(3)}{6}

2cm

$AE = x$
$BAE = 30^{\circ}$ (angles in the same segment are equal)
$x=\frac{2}{\tan(30)}=2\sqrt{3}$

8.39cm (2dp)

6.43cm (2dp)

15.56cm (2dp)

13.05cm (2dp)

$AEB = 90^{\circ}$ ( $AC$ is perpendicular to $BD$ )
$BAE = 40^{\circ}$ (angle in a semicircle is $90^{\circ}$ so $BAD=90^{\circ}$ )
$ABD = 50^{\circ}$ (angles in a triangle total $180^{\circ}$ )
$x=\frac{10}{\tan(50)}=8.39\quad(2dp)$

0.26cm (2dp)

2.43cm (2dp)

4.77cm (2dp)

3.86cm (2dp)

$CBG = 51^{\circ}$ (alternate angles in parallel lines are equal)
$BC = CD = x$ ( $BCD$ is an isosceles triangle)
$x=\frac{3}{\sin(51)}=3.86\quad(2dp)$

14.39cm (2dp)

12.21cm (2dp)

17.46cm (2dp)

9.22cm (2dp)

$BEA = 90^{\circ}$ ( $AC$ is perpendicular to $BD$ )
$BE = DE = 7cm$ ( $BD$ is bisected by the diameter)
$OE=\frac{3}{5}\times{10}=6$
$AE = 10 + 6 = 16cm$
$x=\sqrt{7^{2}+16^{2}}$
$x=17.46cm (2dp)$

\frac{1}{3}cm

3cm

\frac{\sqrt{2}}{6}cm

3\sqrt{2}cm

$OC = OD = x$
$BOC = 90^{\circ}$ ( $AC$ and $BD$ are perpendicular)
where $M$ is the midpoint of $BC$ .
$x=\frac{3}{\sin(45)}=3\sqrt{2}$

8.89cm (2dp)

6.46cm (2dp)

1.02cm (2dp)

41.33cm (2dp)

$ABF = 90^{\circ}$ ( $BF$ is perpendicular to $AD)</li> <li> BGA = 180 - 99 = 81^{\circ}$ (angles on a straight line total $180^{\circ}$ )
$AB = 9sin(81)=8.89cm (2dp)$
$AC=\frac{8}{11}AB$
$AC = 6.46cm (2dp)$

Chord of a circle GCSE questions

1. Below is a triangle inscribed in a circle with centre $O$ . The line $BC$ is parallel to the tangent $DE$ . $BG = 6.2cm$ . Calculate the length of the line $AB$ .

(3 marks)

Show answer

$ABC = 55^{\circ}$ (alternate segment theorem)

(1)

$AGB = 90^{\circ}$ ( $BC$ is perpendicular to $AF$ )

(1)

x=\frac{6.2}{\cos(55)}=10.8cm\quad(1dp)

(1)

2. (a) The circle below has centre O. The diameter BD is perpendicular to the chord AC at point E. CE = 5.4cm and angle AB = 8.1cm. Calculate the length of the line BE.

(b) Calculate the size of the angle ABE. Write your answer to 1 decimal place.

(5 marks)

Show answer

(a)
$AE = CE = 5.4cm$

(1)

BE=\sqrt{8.1^{2}-5.4^{2}}

(1)

BE = 6.04cm (2dp)

(1)

(b)
$ABE=\sin^{-1}(\frac{5.4}{8.1})$

(1)

ABE = 41.8^{\circ} (1dp)

(1)

3. The diagram below shows a circle with the following information:

Centre $O$
$AC$ is a straight line through $B$
$AD = CD$
$DH = 3cm$
$BH = 8cm$

Calculate the length of $BC$ , labelled $x$ .

(5 marks)

Show answer

$CDA = 90^{\circ}$ as the tangent meets the radius at $90^{\circ}$ and $AHB = 90^{\circ}$ as $BF$ is parallel to $CE$

(1)

$AH = BH = 8cm$
$AB=\sqrt{8^{2}+8^{2}}=8\sqrt{2}$

(1)

$AD = CD = 11cm$
Scale factor of enlargement: $11\div8=1.375$

(1)

AC=8\sqrt{2}\times{1.375}=11\sqrt{2}

(1)

11\sqrt{2}-8\sqrt{2}=3\sqrt{2}cm

(1)

Learning checklist

You have now learned how to:

Apply and prove the standard circle theorems concerning angles, radii, tangents and chords, and use them to prove related results

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.