Angles around a point

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

Learn more

In order to access this I need to be confident with:

Types of angles Angles on a straight line Collecting like terms Solving equations 2D shapes

This topic is relevant for:

GCSE Maths Geometry and Measure Angles Angle Rules

Angles Around a Point

Here we will learn about angles around a point, including the sum of angles around a point, how to find missing angles, and using these angle facts to generate equations and solve problems.

There are also angles around a point worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What are angles around a point?

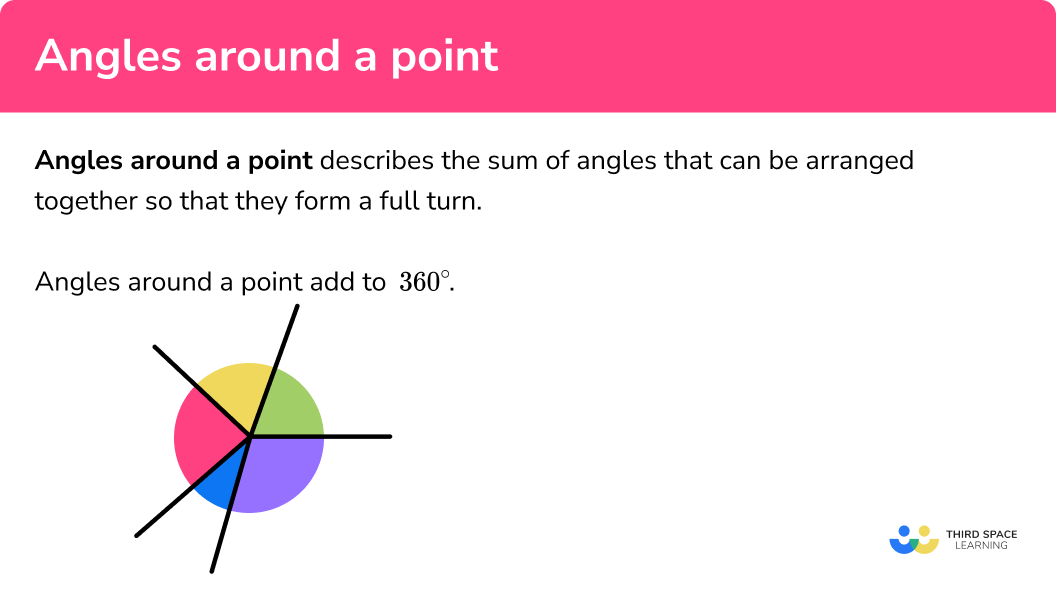
Angles around a point describes the sum of angles that can be arranged together so that they form a full turn. Angles around a point add to 360°.

Let’s look at this visually and take the five angles below:

Rearranging these angles so that they meet at one point or vertex, we get:

The sum of the angles is 360° and they have made a full turn, and so the angles around a point add to equal 360°.

Angles around a point are applied to many problem solving style questions including properties of 2D shapes and 3D shapes including right angles, exterior angles, bearings, angles in parallel lines, pie charts, vertically opposite angles, and more.

What are angles around a point?

How to find missing angles around a point

In order to find missing angles around a point:

Add all known angles.
Subtract the angle sum from 360°.
Form and solve the equation.

How to find missing angles around a point

Angles around a point worksheet

Get your free angles around a point worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Angles around a point worksheet

Get your free angles around a point worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Angles around a point examples

Example 1: reflex angles

The lines A and B meet at the point O. Calculate the missing angle a.

Add all known angles.

\[128^{\circ}\]

2Subtract the angle sum from 360°.

\[360-128=232^{\circ}\]

\[x=232^{\circ}\]

Example 2: multiple angles around a point

Calculate the size of angle x.

Add all known angles.

\[151+64+90=305^{\circ}\]

Subtract the angle sum from 360°.

\[360-305=55^{\circ}\]

\[x=55^{\circ}\]

Example 3: bearings

A ship is facing East. How far does the ship need to turn in the clockwise direction to face North West?

Add all known angles.

The angle between North West and North is a turn of 45° (you should be able to work this out from the diagram as it is half of a quarter turn).

\[45+90=135^{\circ}\]

Subtract the angle sum from 360°.

\[360-135=225^{\circ}\]

\[x=225^{\circ}\]

Example 4: reflex angle inside a polygon

ABCD is an arrowhead. Calculate the missing angle c.

Add all known angles.

The sum of angles in a quadrilateral is equal to 360°. We need to use this fact first to determine the reflex angle of BCD.

\[16+27+27=70^{\circ}\]

\[360-70^{\circ}=290^{\circ}\]

The reflex angle at C = 290^o.

Subtract the angle sum from 360°.

\[360-290=70^{\circ}\]

\[c=70^{\circ}\]

Example 5: forming and solving equations

The point O is surrounded by five angles shown in the diagram below. Calculate the value of x.

Add all known angles.

\[8x+4x+5x+8+5x-7+7x+11=29x+12\]

Form and solve the equation.

Angles around a point add to 360° so we have the equation 29x + 12 = 360.

\[4x=412=48^{\circ}\]

\[5x+8=512+8=68^{\circ}\]

\[5x-7=512-7=53^{\circ}\]

\[7x+11=712+11=95^{\circ}\]

\[8x=812=96^{\circ}\]

We can check the solution by adding up the angles:

\[48+68+53+95+96=360^{\circ}\]

Example 6: angles in parallel lines

Calculate the exact value of y.

Add all known angles.

Using angle facts in parallel lines, we can state other angles in the diagram shown below:

This means we have a point surrounded by angles that we can add together:

\[3x-12+y+2x+21+y=5x+2y+9\]

So,

\[5x+2y+9=360\]

Or:

\[5x+2y=351\]

Form and solve the equation.

The vertically opposite angles of 3x – 12 and 2x + 21 are equal so we can solve:

Substituting x = 33 into our equation from earlier we get:

\[5\times33+2y=351\\ 2y=186\\ y=93^{\circ}\]

Common misconceptions

Confusing the sum of angles around a point and angles on a straight line

The angle sum is remembered incorrectly as 180°, rather than 360°. The sum of angles around a point is one full turn, or 360°.

Incorrectly assuming the diagram is accurately drawn

The reflex angle in a diagram is incorrectly assumed to be double the other angle around a point.

E.g. in example 1

the reflex angle is calculated as 12×82=256°

Solving equations

There are many misconceptions around forming and solving equations. See the lesson on forming and solving equations for further information.

Step by step guide: Solving equations

Using a protractor

When you are asked to calculate a missing angle, a common error is to use a protractor to measure the angle. When using angle facts to determine angles, diagrams are deliberately not drawn to scale unless the angle is 90° or 180° as these are important angles to recognise. You do not use a protractor for this style of question.

Angles around a point is part of our series of lessons to support revision on angle rules. You may find it helpful to start with the main angle rules lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Practice angles around a point questions

x=76^{\circ}

x=256^{\circ}

x=208^{\circ}

x=104^{\circ}

260-104=256^{\circ}

x=22^{\circ}

x=24^{\circ}

x=112^{\circ}

x=12^{\circ}

182+90+66=338^{\circ}\\ 360-338=22^{\circ}

45^{\circ}

225^{\circ}

270^{\circ}

135^{\circ}

The angle between North West and North is a turn of $45^{\circ}$ . The angle between North and East is equal to $90^{\circ}$ , so $45+90=135^{\circ}$ .

BOF=140^{\circ}

BOF=120^{\circ}

BOF=80^{\circ}

BOF=40^{\circ}

x=25^{\circ}, giving angles  75^{\circ}, 100^{\circ}, 107^{\circ}, 172^{\circ}, 181^{\circ}

x=12.56^{\circ}, giving angles 37.68^{\circ}, 50.24^{\circ}, 44.8^{\circ}, 97.36^{\circ}, 93.92^{\circ}

x=14^{\circ}, giving angles 42^{\circ}, 56^{\circ}, 52^{\circ}, 106^{\circ}, 104^{\circ}

x=10.3^{\circ}, giving angles 30.9^{\circ}, 41.2^{\circ}, 33.5^{\circ}, 83.8^{\circ}, 78.1^{\circ}

x=165^{\circ}

x=15^{\circ}

x=345^{\circ}

x=195^{\circ}

Angles on a straight line: $180-95=85^{\circ}$

Corresponding angles: $85^{\circ}$

Angles on a straight line: $180-100=80^{\circ}$

Angles in a triangle: $180-(85+80)=15^{\circ}$

Angles around a point: $360-15=345^{\circ}$

Angles around a point GCSE questions

1. Calculate the size of the angle $y$ .

(2 marks)

Show answer

$90+97=187$

(1)

$360-187=173^{\circ}$

(1)

(a) Three regular hexagons are placed in the following format:

Show that each of the $6$ triangles that make up one hexagon is an equilateral triangle.

(b) Calculate the size of angle $x$ .

(6 marks)

Show answer

a)

Regular hexagons have equal side lengths and equal angles

(1)

The regular hexagons tessellate so $360\div6=60^{\circ}$

(1)

Alternate angles are the same at $60^{\circ}$

(1)

All interior angles equal $60^{\circ}$

(1)

$60+60=120$

(1)

$360-120=240^{\circ}$

(1)

3. Tim is practicing using a compass. He takes $10$ steps on a bearing of $180^{\circ}$ , followed by $10$ steps at a bearing of $090^{\circ}$ . He then turns $200^{\circ}$ anticlockwise.

What bearing is he now facing?

(3 marks)

Show answer

$180^{\circ}$ is South, $090^{\circ}$ is East

(1)

$200^{\circ}$ anticlockwise = $360-200=160^{\circ}$ clockwise

(1)

$090+160=250^{\circ}$

(1)

Learning checklist

You have now learned how to:

Find unknown angles around a point

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.