Complementary angles

GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

Teacher-trusted tutoring

In order to access this I need to be confident with:

Angle rules Types of angles Angles on a straight line

This topic is relevant for:

GCSE Maths Geometry and Measure Angles Angle Rules

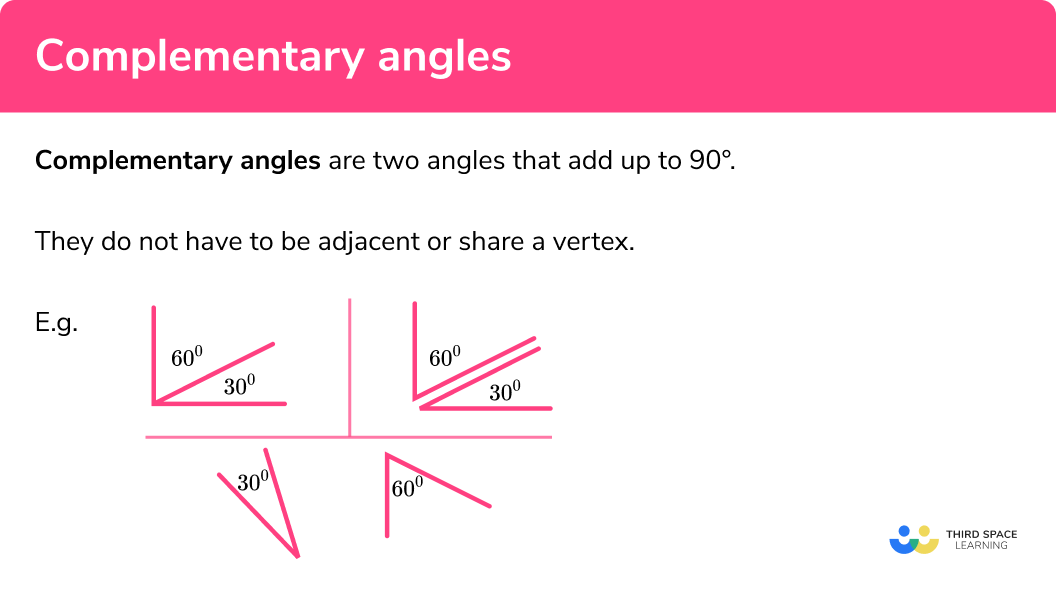
Complementary Angles

Here we will learn about complementary angles including how to find missing angles by applying knowledge of complementary angles to a context.

There are also angles worksheets based on Edexcel, AQA and OCR GCSE exam style questions, along with further guidance on where to go next if you’re still stuck.

What are complementary angles?

Complementary angles are two angles that add up to 90 degrees. They do not have to be adjacent or share a vertex.

E.g.

When we add together complementary angles we get a right angle.

Before we start looking at specific examples it is important we are familiar with some key words, terminology, rules and symbols required for this topic:

Angle: defined as the amount of turn around a common vertex.
Vertex: the point created by two line segments (plural is vertices).

How to label an angle:

We normally label angles in two main ways:

By giving the angle a ‘name’ which is normally a lowercase letter/symbol such as a, x or y or the greek letter (theta).

2By referring to the angle as the three letters that define the angle. The middle letter refers to the vertex at which the angle is e.g. see the diagram for the angle we call ABC:

Angles on a straight line equal 180°:

Angles on one part of a straight line always add up to 180°.

However in the diagram below a and b do not equal 180° because they are not on one single part of a straight line, i.e. they do not share a vertex and are not adjacent to one another:

Angles around a point will always equal 360°. See the diagram for an example where angles a, b and c are equal to 360°:

Vertically opposite angles:

Vertically opposite angles refer to angles that are opposite one another at a specific vertex and are created by two lines crossing. See below for an example:

Here the two angles labelled ‘a’ are equal to one another because they are ‘vertically opposite’ at the same vertex.

The same applies to angles labelled as ‘b’.

Note: Sometimes these are called vertical angles.

What are complementary angles?

How to solve problems involving complementary angles

In order to solve problems involving complementary angles:

Identify which angles are complementary.
If appropriate write this down using angle notation e.g. AOC + BOC = 90°
Clearly identity which of the unknown angles the question is asking you to find the value of.
Solve the problem and give reasons where applicable.
Clearly state the answer using angle terminology.

How to solve problems involving complementary angles

Complementary and supplementary angles worksheet

Get your free complementary and supplementary angles worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Complementary and supplementary angles worksheet

Get your free complementary and supplementary angles worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Complementary Angles examples

Example 1: finding an angle which is complementary to another

Two angles ‘x and y‘ are complementary and one of them is 17°. What is the size of the other angle?

Identify which angles are complementary.

The two angles are complementary and therefore equal 90°

\[x+y=90\]

2Clearly identity which of the unknown angles the question is asking you to find the value of.

Find the angle that is not 17°.

3Solve the problem and give reasons where applicable.

\[\begin{aligned} x+y&=90 \\ x+17&=90 \\ x&=73 \end{aligned}\]

4Clearly state the answer using angle terminology.

The size of the other angle is 73°.

Example 2: finding an angle which is complementary to another

Two angles are complementary. One is double the size of the other. What is the size of the smaller angle?

Identify which angles are complementary.

The two non-identified angles are complementary and therefore equal 90°.

Clearly identity which of the unknown angles the question is asking you to find the value of.

You are being asked to find the smaller angle.

Solve the problem and give reasons where applicable.

If you call the first angle ‘a‘ then the other angle must be 2a as ‘one is double the size of the other.’ Therefore a + 2a = 90.

We can now solve this equation:

\[\begin{aligned} a+2a&=90 \\ 3 a&=90 \hspace{3cm} \text{simplify the equation} \\ a&=30 \hspace{3cm} \text{divide each side of the equation by 3} \end{aligned}\]

The two angles are therefore of size 30° and 60°.

Clearly state the answer using angle terminology.

The smaller angle is 30°.

Example 3: finding complementary angles from a diagram

ABC is a right-angled triangle. Which of the following pair of angles is complementary?

Identify which angles are complementary.

In this question you are not told which angles are complementary.

Clearly identity which of the unknown angles the question is asking you to find the value of.

You are trying to find the angles that are complementary. Therefore we are looking for two angles that when added together equal 90°.

Solve the problem and give reasons where applicable.

We know the sum of interior angles for a triangle is 180° and in a right angle triangle one of the angles is 90°. Consequently we can deduce that the other two angles must also be equal to 90° and therefore be complementary.

Clearly state the answer using angle terminology.

Angles ABC and BCA are complementary.

Example 4: finding a given angle using complementary angles

Angles A and B are complementary to one another.

\[A = 2x – 8\]

\[B = 5x – 7\]

Find the size of angle A.

Identify which angles are complementary.

The two angles given as A and B are complementary and therefore equal 90°.

Therefore A + B = 90°.

Clearly identity which of the unknown angles the question is asking you to find the value of.

Find the size of angle A.

Solve the problem and give reasons where applicable.

We can create an equation from the information given:

\[\begin{aligned} A+B&=90 \\ 2 x-8+5 x-7&=90 \\ 7 x-15&=90 \\ 7 x&=105 \\ x&=15 \end{aligned}\]

Remember you need to find the value of angle A so we substitute the value x = 15 into the expression for angle A:

\[\begin{aligned} A=2x-8\\ A=2(15)-8\\ A=30-8\\ A=22 \end{aligned}\]

Clearly state the answer using angle terminology.

Angle A = 22°.

Example 5: identifying complementary angles within a polygon

ABCD is a rectangle. Which of these is a pair of complementary angles: DAB and DCB or DAC and CAB?

Identify which angles are complementary.

In this question you are not told which angles are complementary.

Clearly identity which of the unknown angles the question is asking you to find the value of.

You are trying to find the angles that are complementary and therefore you are looking for two angles that when added together equal 90°. Remember you are given a choice of DAB and DCB or DAC and CAB.

Solve the problem and give reasons where applicable.

Below is the diagram (given in the question) where the two sets of angles have been labelled separately. This will help you spot which are complementary

DAB (top left angle) and DCB (bottom right angle)

The two angles labelled are both right angles as they are created by adjacent line segments of a rectangle. Therefore when added together they make 180 degrees, and are subsequently supplementary angles not complementary angles.

DAC (green angle) and CAB (blue angle)

The diagram shows the two angles make a right angle and are therefore complementary

Clearly state the answer using angle terminology.

Angle DAC and CAB are complementary.

Example 6: complementary angles within a polygon

Can a parallelogram contain a pair of complementary angles? If so state their size.

Identify which angles are complementary.

In this question you are not told which angles are complementary.

Clearly identity which of the unknown angles the question is asking you to find the value of.

You are being asked to find whether a parallelogram contains a pair of angles that when added together equal to 90°. A diagram is below:

Solve the problem and give reasons where applicable.

The interior angles at vertex A and C are obtuse and therefore cannot be part of a complementary angle pair.

The interior angles at vertex D and B are equal to one another (congruent) and acute angles. Therefore to be complementary they would have to be 45° each.

Clearly state the answer using angle terminology.

A parallelogram can contain complementary angles.

The two acute angles in the parallelogram would be 45° each.

Common misconceptions

Incorrectly labelling angles which are complementary
Assuming complementary angles must share a vertex
Mixing up complementary angles and supplementary angles
Misuse of the ‘straight line’ rule where angles do not share a vertex
Finding the incorrect angle due to misunderstanding the terminology

Complementary angles is part of our series of lessons to support revision on angle rules. You may find it helpful to start with the main angle rules lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Practice complementary angles questions

x=33

x=43

x=133

x=313

If two angles are complementary, they add up to $90$ , $43+47=90$ .

x=3

x=87

x=93

x=177

If two angles are complementary, they add up to $90$ , $3+87=90$

20^{\circ}

36^{\circ}

18^{\circ}

72^{\circ}

The angles make up a $90$ degree angle. There are four parts in one angle and one part in the other, so five parts in total. If we divide $90$ by $5$ we get $18$ , so this is the size of the smaller angle.

x=16

x=29

x=45

x=90

The sum of the two angles must equal $90$ , so the equation we must solve is $3x-45=90$ . Using the standard methods for solving a linear equation gives the solution $x=45$ .

33^{\circ}

22^{\circ}

68^{\circ}

79^{\circ}

The sum of the two angles must equal $90$ , so the equation we must solve is $7x-64=90$ . Using the standard methods for solving a linear equation gives the solution $x=22$ so the two angles are $11^{\circ}$ and $79^{\circ}$

Yes

Since each corner of a rectangle is a right angle, it is not possible for any two angles to add up to $90$ .

Complementary Angles GCSE questions

1. Find the size of the angle marked $a$ :

(2 marks)

Show answer

90-61

(1)

29^{\circ}

(1)

2. Are angles $x$ and $y$ complementary? Give reasons for your answer.

(3 marks)

Show answer

135 + 135 = 270

(1)

 $360-270 = 90$  - angles in a quadrilateral add to  $360^{\circ}$

(1)

Yes they are complementary as they add up to  $90^{\circ}$

(1)

3. Find the size of the larger angle:

(4 marks)

Show answer

3x + 5x + 2 = 90

(1)

8x + 2 = 90

(1)

\begin{aligned} 8x&=88\\ x&=11 \end{aligned}

(1)

5 \times 11 + 2 = 57

(1)

Learning checklist

You have now learned how to:

Use conventional terms and notation for angles

Define angles that are complementary

Apply the properties of complementary angles

Apply angle facts and properties to solve problems

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Introduction

What are complementary angles?

How to solve problems involving complementary angles

Complementary angles worksheet

Complementary angles examples

↓

Example 1: finding an angle which is complementary to another Example 2: finding an angle which is complementary to another Example 3: finding complementary angles from a diagram Example 4: finding a given angle using complementary angles Example 5: identifying complementary angles within a polygon Example 6: complementary angles within a polygon

Common misconceptions

Related lessons

Practice complementary angles questions

Complementary angles GCSE questions

Learning checklist

Next lessons

Still stuck?