One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
In order to access this I need to be confident with:
Tangent of a circle Equation of a circle Circle graph Parallel and perpendicular lines Gradient of a line Equation of a line Equations with fractionsThis topic is relevant for:

Equation Of Tangent
Here we will learn about the equation of a tangent, including finding the equation of a tangent of a circle.
There is also an equation of a tangent worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is the equation of a tangent?
The equation of a tangent line is the equation of the straight line touching the circumference of the circle at only one point, known as the tangent. A line is only a tangent if there is exactly one point of contact between the straight line and the circle.
To find the equation of a tangent, we first need to be able to find the gradient of the radius of the circle – we use the gradient formula for finding the gradient of a line segment joining two points,
m=\cfrac{y_{2}-y_{1}}{x_{2}-x}to find the gradient of the radius (m_{1}).
Step-by-step guide: Gradient of a line
We know from work on circle theorems that the angle between the radius of a circle and the tangent line at a given point is 90 degrees – these two lines are perpendicular.
We then use knowledge of circle theorems and perpendicular lines to find the gradient of the tangent (m_{2}) as follows,
- the tangent and radius are perpendicular,
- the product of perpendicular gradients is -1
(i.e. m_{1} m_{2}=-1 ), - rearranging this gives the gradient of the tangent m_{2}=\cfrac{-1}{m_{1}}.
Alternatively, it may help to think of the gradient of the tangent as the negative reciprocal of the gradient of the radius – so find the reciprocal, then multiply by -1, which has the effect of changing the sign.
For example, if the gradient of the radius is the fraction \cfrac{4}{3}, we would find the reciprocal, which is \cfrac{3}{4}, then multiply by -1 to give the gradient of the tangent as -\cfrac{3}{4}.
Step-by-step guide: Parallel and perpendicular lines
Finally we find the y -intercept of the tangent by substituting our known values into the equation y=mx+c and solving to find c. This completes the full equation of the tangent to the circle.
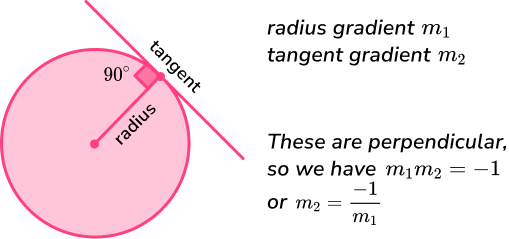
When working with circle equations at GCSE, you are only expected to deal with examples where the centre of the circle is at the origin (0,0). These ideas are extended to any circle with a non-zero centre in A Level maths.
However, when finding the equation of a tangent, you may be expected to work with circles with a non-zero centre – this is because the method used is identical whether the circle is centred at the origin or elsewhere on the coordinate grid. You can see this in example 5 below.
What is the equation of a tangent?
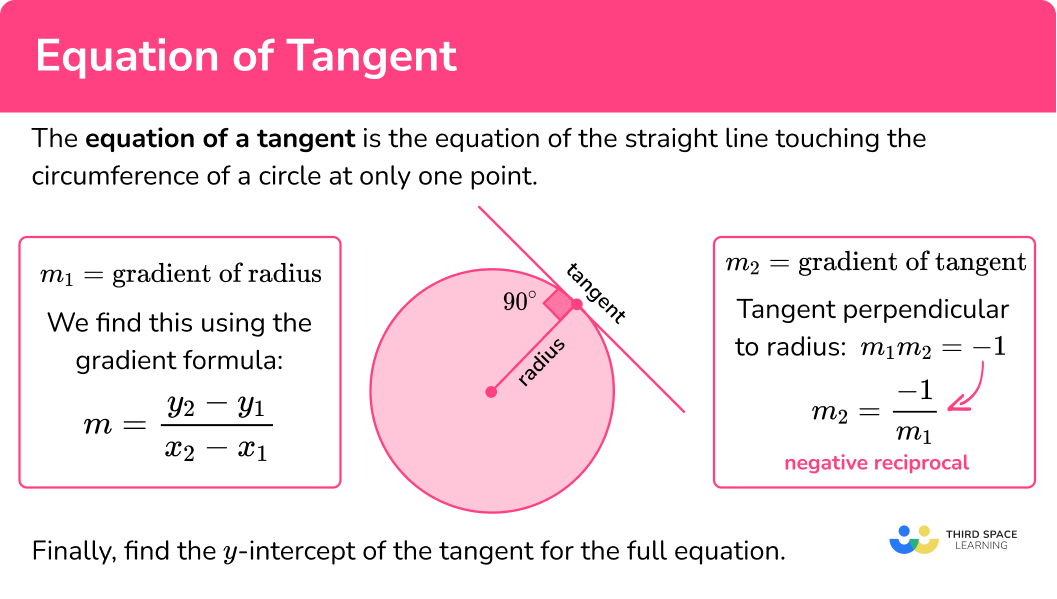
How to find the equation of a tangent
In order to find the equation of the tangent to a circle at a given point:
- Find the gradient of the radius at that point.
- Find the gradient of the tangent at that point.
- Find the \textbf{y} -intercept and hence the equation of the tangent.
Explain how to find the equation of a tangent

Equation of tangent to a circle worksheet

Get your free equation of tangent to a circle worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Equation of tangent to a circle worksheet

Get your free equation of tangent to a circle worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREERelated lessons on circles, sectors and arcs
Equation of tangent is part of our series of lessons to support revision on parts of a circle and circles, sectors and arcs. You may find it helpful to start with the main circles, sectors and arcs lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Equation of tangent examples
Example 1: finding the equation of a tangent
Find the equation of the tangent to the circle x^{2}+y^{2}=90 at the point (9,3).
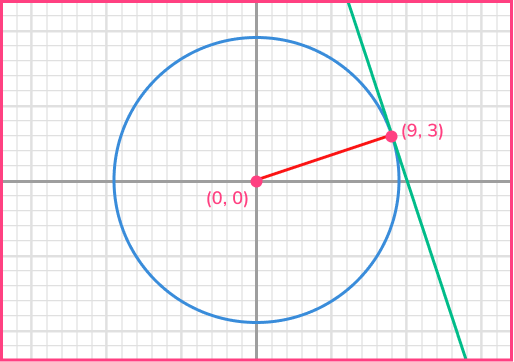
- Find the gradient of the radius at that point.
The radius is the line joining the centre of the circle (0,0) and the known point on the circumference (9,3).
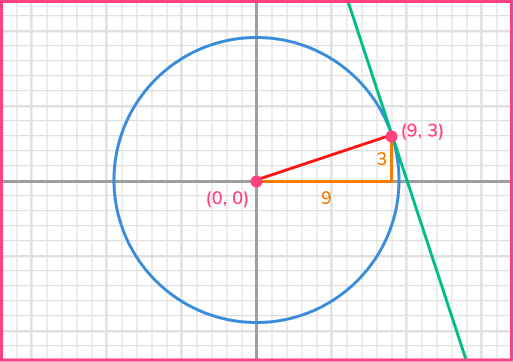
To find the gradient of the radius, calculate m=\cfrac{y_{2}-y_{1}}{x_{2}-x_{1}}.
m=\cfrac{y_{2}-y_{1}}{x_{2}-x_{1}}=\cfrac{3-0}{9-0}=\cfrac{3}{9}=\cfrac{1}{3}2Find the gradient of the tangent at that point.
The gradient of the radius =\cfrac{1}{3}.
The reciprocal of =\cfrac{1}{3} is 3.
Multiply this by -1 (change the sign) to get the gradient of the tangent, gradient =-3.
3Find the \textbf{y} -intercept and hence the equation of the tangent.
We now have the gradient of the tangent line, -3, so we know the equation of the line is y=-3x+c.
We use the known point on that line (9,3) to find c.
We substitute the values x=9 and y=3 into y=-3x+c and solve for c.
\begin{aligned} 3 &=-3(9)+c \\\\ 3 &=-27+c \\\\ 30 &=c \end{aligned}Hence the equation of the tangent is y=-3x+30, or, better, y=30-3x.
Example 2: finding the equation of a tangent
Find the equation of the tangent to the circle x^{2}+y^{2}=80 at the point (-4,8).
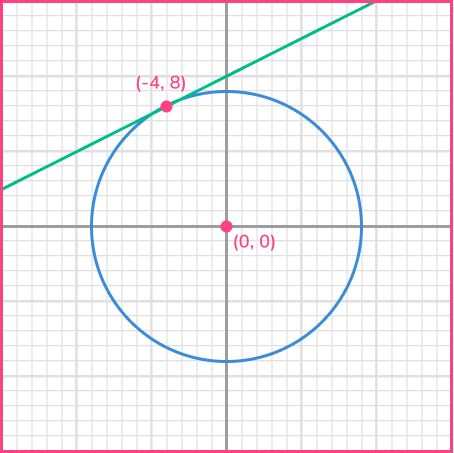
Find the gradient of the radius at that point.
The radius is the line joining the centre of the circle (0,0) and the known point on the circumference (-4,8).
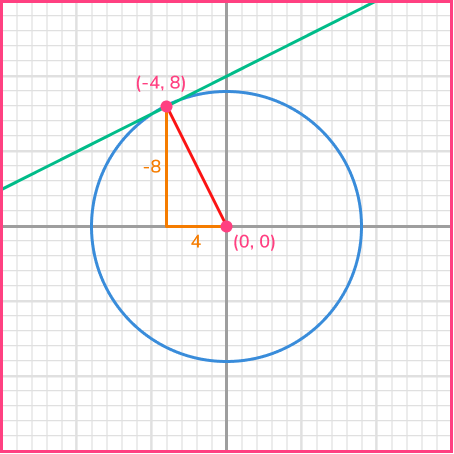
To find the gradient of the radius, calculate m=\cfrac{y_{2}-y_{1}}{x_{2}-x_{1}}.
m=\cfrac{y_{2}-y_{1}}{x_{2}-x_{1}}=\cfrac{0-8}{0–4}=\cfrac{-8}{4}=-2
Find the gradient of the tangent at that point.
The gradient of the radius =-2.
The reciprocal of -2 is -\cfrac{1}{2}.
Multiply this by -1 (change the sign) to get the gradient of the tangent, gradient =\cfrac{1}{2}.
Find the \textbf{y} -intercept and hence the equation of the tangent.
We now have the gradient of the tangent line, \cfrac{1}{2}, so we know the equation of the line is y= \cfrac{1}{2} x+c.
We use the known point on that line (-4,8) to find c.
We substitute the values x=-4 and y=8 into y= \cfrac{1}{2}x+c and solve for c.
\begin{aligned} 8 &=\cfrac{1}{2}(-4)+c \\\\ 8 &=-2+c \\\\ 10 &=c \end{aligned}
Hence the equation of the tangent is y=\cfrac{1}{2} x+10.
Example 3: dealing with trickier fractions
Find the equation of the tangent to the circle x^{2}+y^{2}=25 at the point (4,3).
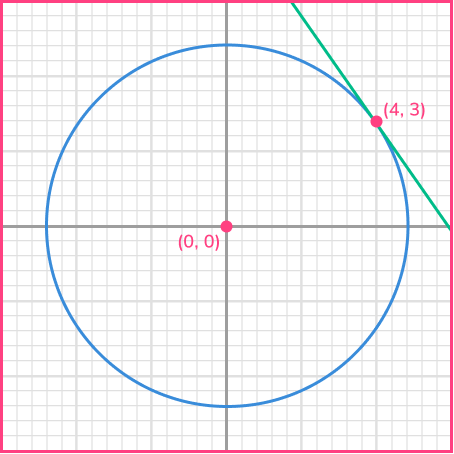
Find the gradient of the radius at that point.
The radius is the line joining the centre of the circle (0,0) and the known point on the circumference (4,3).
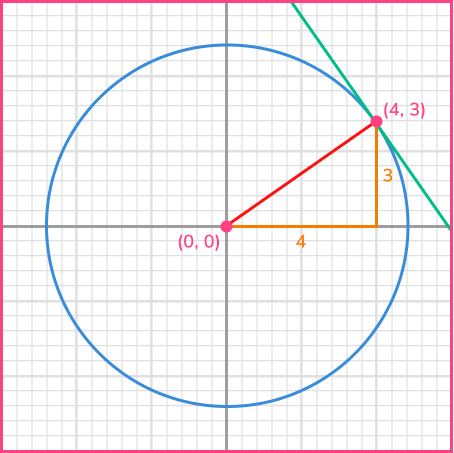
To find the gradient of the radius, calculate m=\cfrac{y_{2}-y_{1}}{x_{2}-x_{1}}.
m=\cfrac{y_{2}-y_{1}}{x_{2}-x_{1}}=\cfrac{3-0}{4-0}=\cfrac{3}{4}
Find the gradient of the tangent at that point.
The gradient of the radius =\cfrac{3}{4}.
The reciprocal of \cfrac{3}{4} is \cfrac{4}{3}.
Multiply this by -1 (change the sign) to get the gradient of the tangent, gradient =-\cfrac{4}{3}.
Find the \textbf{y} -intercept and hence the equation of the tangent.
We now have the gradient of the tangent line, =-\cfrac{4}{3}, so we know the equation of the line is y=-\cfrac{4}{3} x+c.
We use the known point on that line (4,3) to find c.
We substitute the values x=4 and y=3 into y= -\cfrac{4}{3}x+c and solve for c.
\begin{aligned} &3=-\cfrac{4}{3}(4)+c \\\\ &3=-\cfrac{16}{3}+c \end{aligned}
It is useful to write 3=\cfrac{9}{3} to be able to rearrange the next step.
\begin{aligned} \cfrac{9}{3} &=-\cfrac{16}{3}+C \\\\ \cfrac{25}{3} &=C \end{aligned}
Hence the equation of the tangent in the form y=mx+c (sometimes called slope intercept form) is y=-\cfrac{4}{3} x+\cfrac{25}{3}.
In cases like this with fractional coefficients, it is also acceptable to multiply by 3 and rearrange to write the final answer as follows,
\begin{aligned} y &=-\cfrac{4}{3} x+\cfrac{25}{3} \\\\ 3 y &=-4 x+25 \\\\ 3 y+4 x &=25 \end{aligned}
An answer in the standard form ax+by=d or ax+by+d=0 is usually much easier to work with if you’re expected to do more with the equation, such as find a point of intersection (see example 4).
Example 4: finding the point of intersection on the x axis
The diagram shows the circle x^{2}+y^{2}=225.
The tangent to the circle at the point (9,12) intersects the x axis at point A.
Find the x coordinate of point A.
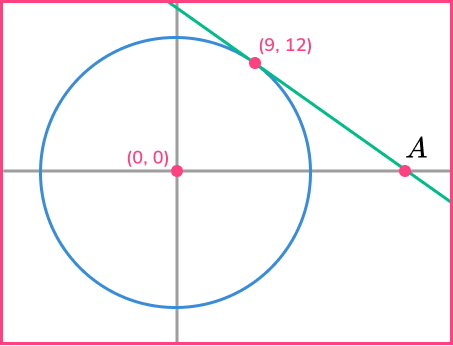
Find the gradient of the radius at that point.
The radius is the line joining the centre of the circle (0,0) and the known point on the circumference (9,12).
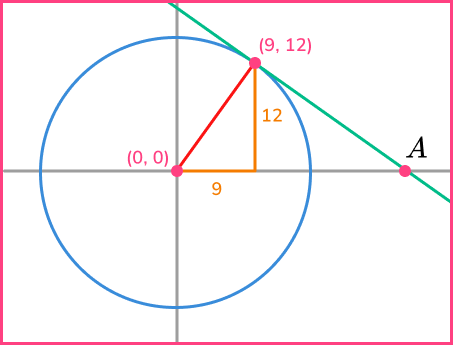
To find the gradient of the radius, calculate m=\cfrac{y_{2}-y_{1}}{x_{2}-x_{1}}.
m=\cfrac{y_{2}-y_{1}}{x_{2}-x_{1}}=\cfrac{12-0}{9-0}=\cfrac{4}{3}
Find the gradient of the tangent at that point.
The gradient of the radius =\cfrac{4}{3}.
The reciprocal of \cfrac{4}{3} is \cfrac{3}{4}.
Multiply this by -1 (change the sign) to get the gradient of the tangent =-\cfrac{3}{4}.
Find the \textbf{y} -intercept and hence the equation of the tangent.
We now have the gradient of the tangent line, -\cfrac{3}{4}, so we know the equation of the line is y=-\cfrac{3}{4} x+c.
We use the known point on that line (9,12) to find c.
We substitute the values x=9 and y=12 into y= -\cfrac{3}{4}x+c and solve for c.
\begin{aligned} &12=-\cfrac{3}{4}(9)+c \\\\ &12=-\cfrac{27}{4}+c \end{aligned}
It is useful to write 12=\cfrac{48}{4} to be able to rearrange the next step.
\begin{aligned} &\cfrac{48}{4}=-\cfrac{27}{4}+C \\\\ &\cfrac{75}{4}=C \end{aligned}
Hence the equation of the tangent is y=-\cfrac{3}{4} x+\cfrac{75}{4}.
Because we have a further step to complete, we can multiply by 4 and rearrange to write the equation in the form,
4y+3x=75.
Substitute \bf{y=0} to find the \textbf{x} value of the point of intersection.
The tangent intersects the x axis at point A, we know that y=0 because this is the value of y all along the x axis.
We substitute y=0 into the equation of the tangent.
\begin{array}{r} 4 y+3 x=75 \\\\ 4(0)+3 x=75 \\\\ 3 x=75 \\\\ x=25 \end{array}
Hence the x coordinate of point A is 25.
Example 5: finding the equation of a tangent with a non-zero centre
The centre of a circle has the coordinates (-1,2). The point (3,5) lies on the circumference of the circle. Find an equation of the tangent to the circle at this point.
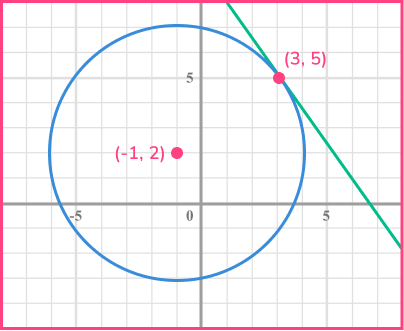
Find the gradient of the radius at that point.
The radius is the line joining the centre of the circle (-1,2) and the known point on the circumference (3,5).
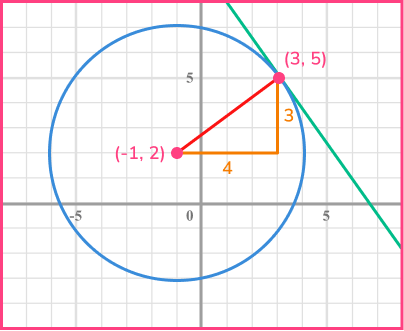
To find the gradient of the radius, calculate m=\cfrac{y_{2}-y_{1}}{x_{2}-x_{1}}.
m=\cfrac{y_{2}-y_{1}}{x_{2}-x_{1}}=\cfrac{5-2}{3-(-1)}=\cfrac{3}{4}
Find the gradient of the tangent at that point.
The gradient of the radius =\cfrac{3}{4}.
The reciprocal of =\cfrac{3}{4} is \cfrac{4}{3}.
Multiply this by -1 (change the sign) to get the gradient of the tangent, gradient =-\cfrac{4}{3}.
Find the \textbf{y} -intercept and hence the equation of the tangent.
We now have the gradient of the tangent line, -\cfrac{4}{3}, so we know the equation of the line is y=-\cfrac{4}{3}x+c.
We use the known point on that line (3,5) to find c.
We substitute the values x=3 and y=5 into y=-\cfrac{4}{3} x+c and solve for c.
\begin{aligned} 5 &=-\cfrac{4}{3}(3)+c \\\\ 5 &=-4+c \\\\ 9 &=c \end{aligned}
Hence the equation of the tangent is y=-\cfrac{4}{3}x+9.
As this equation contains a fraction, it is better to rewrite in the form ax+by=d, so we multiply by 3 and rearrange to give
\begin{aligned} 3 y &=-4 x+27 \\\\ 4 x+3 y &=27 \end{aligned}
Hence the equation of the tangent to the circle at the given point is 4x+3y=27.
Proof using equation of a tangent
Sometimes you might be asked to prove statements about equations of tangents, such as proving that a given line is tangent to a given circle.
For example, you might be asked to prove algebraically that the straight line 2x+y=20 is a tangent to the circle with equation x^{2}+y^{2}=80.
Notice that we have two equations with two unknowns, so we are solving simultaneous equations. As the equation of a circle involves squared terms, we are in fact solving a pair of simultaneous equations where one is linear and the other one quadratic.
Step-by-step guide: Quadratic simultaneous equations
In this case, we rearrange the linear equation 2x+y=20 to give us a statement we can substitute into the circle equation, in order to eliminate one variable and form a quadratic equation that we can solve using standard methods.
We know that the tangent to a circle only touches the circle at one point; this means that if the line given is a tangent, we should only obtain one solution to the quadratic equation. As we are writing a proof, the final line needs to be a statement that we have shown this to be true.
How to prove that a line is a tangent to a circle
In order to prove that a line is a tangent to a circle:
- Rearrange the linear equation and substitute into the equation of the circle to get a quadratic.
- Simplify and solve the quadratic equation.
- Make a statement about the solution.
Explain how to prove that a line is a tangent to a circle

Proof using equation of tangent examples
Example 6: proving that a line is a tangent to a circle
Prove algebraically that the straight line 2x+y=20 is a tangent to the circle with equation x^{2}+y^{2}=80.
Rearrange the linear equation and substitute into the equation of the circle to get a quadratic.
We can rearrange 2x+y=20 to make either x or y the subject – it doesn’t matter which we choose. Here we will rearrange to make y the subject because this requires fewer steps.
\begin{aligned} 2x+y&=20 \\ y&=20-2x \end{aligned}
Then substitute this expression for y into the equation of the circle.
\begin{aligned} x^{2}+y^{2}&=80 \\ x^{2}+(20-2x)^{2}&=80 \end{aligned}
Simplify and solve the quadratic equation.
We now expand (20-2x)^2 and simplify to get a standard quadratic to solve.
\begin{aligned} (20-2x)^2&=(20-2x)(20-2x) \\ &=400-40x-40x+4x^2 \\ &=4x^2-80x+400 \end{aligned}
\begin{aligned} x^2+(4x^2-80x+400)&=80 \\5x^2-80x+400&=80 \end{aligned}
To solve this quadratic, we need one side (here the RHS) to equal zero, so subtract 80 from both sides,
5x^{2}-80x+320=0.
Notice that each coefficient is a multiple of 5, so we can divide through by 5 to make the numbers smaller and easier to deal with,
x^{2}-16x+64=0.
Finally, solve the quadratic. We do this by factorisation here, although you could use either of the other two methods (completing the square or the quadratic formula).
\begin{aligned} x^{2}-16x+64&=0 \\ (x-8)(x-8)&=0 \end{aligned}
We have one solution, x=8.
In situations like this one where you are told that a line is a tangent and asked to prove it, you should expect to see a repeated root and one solution, so look out for this when factorising.
Make a statement about the solution.
Because we are writing a proof, we need to end our mathematical working with a statement.
Here we write,
the line and the circle intersect at one point (x=8), so the line must be a tangent to the circle.
If you wanted to, you could substitute the x value into either equation to find the corresponding y value, and hence the coordinates of the point of intersection – but this isn’t necessary for this particular question.
Common misconceptions
- Using the gradient of the radius rather than the gradient of the tangent in the final equation
Be careful that you don’t miss out a step – the gradient of the radius enables us to use perpendicularity to then find the gradient of the tangent.
- Dividing the wrong way round when calculating gradients
Remember that the gradient is calculated as \cfrac{\text{ change in y}}{\text{change in x}}.
- Forgetting to change the sign when finding the perpendicular gradient
The gradient of the tangent is the negative reciprocal of the gradient of the radius.
Practice equation of tangent questions
1. Find the equation of the tangent to the circle x^{2}+y^{2}=45 at the point (-6,3).
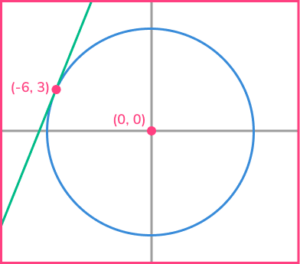




The gradient of the radius is -\cfrac{1}{2}, so the gradient of the tangent is 2.
Substitute x=-6 and y=3 into y=2x+c to get the answer y=2x+15.
2. Find the equation of the tangent to the circle x^{2}+y^{2}=40 at the point (-6,2).
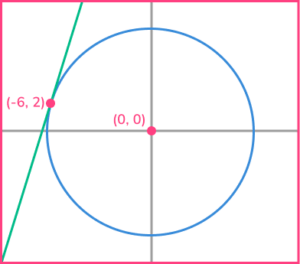




The gradient of the radius is -\cfrac{1}{3}, so the gradient of the tangent is 3.
Substitute x=-6 and y=2 into y=3x+c to get the answer y=3x+20.
3. Find the equation of the tangent to the circle x^{2}+y^{2}=52 at the point (6,-4).
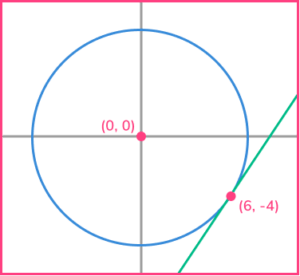




The gradient of the radius is -\cfrac{2}{3}, so the gradient of the tangent is \cfrac{3}{2}.
Substitute x=6 and y=-4 to get the answer y=\cfrac{3}{2}x-13.
4. Find the equation of the tangent to the circle x^{2}+y^{2}=50 at the point (1,-7).
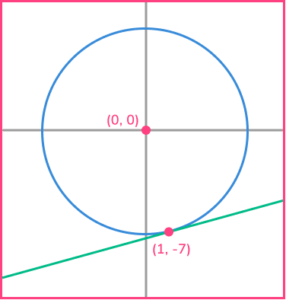
Write your answer in the form ax+by+d=0.




The gradient of the radius is -7, so the gradient of the tangent is \cfrac{1}{7}.
Substitute x=1 and y=-7 to get the answer y=\cfrac{1}{7} x-\cfrac{50}{7},
then multiply by 7, giving 7y=x-50 and rearrange to the correct form.
5. The diagram shows the circle x^{2}+y^{2}=40.
The tangent to the circle at the point (2,6) intersects the x axis at point A.
Find the x coordinate of point A.
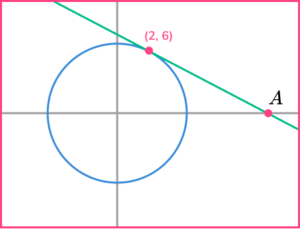




The gradient of the radius is 3, so the gradient of the tangent is -\cfrac{1}{3}.
Substitute x=2 and y=6 to get the answer x+3y=20.
Then substitute y=0 to get x=20.
6. The diagram shows the circle x^{2}+y^{2}=100.
The tangent to the circle at the point (-8,6) intersects the x axis at point A.
Find the x coordinate of point A.
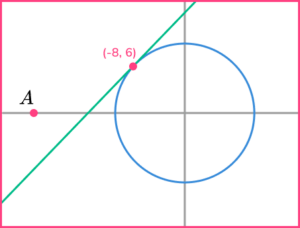




The gradient of the radius is -\cfrac{3}{4}, so the gradient of the tangent is \cfrac{4}{3}.
Substitute x=-8 and y=6 to get the answer 4x-3y+50=0.
Then substitute y=0 to get x=-\cfrac{25}{2} or -12.5.
Equation of tangent GCSE questions
1. Here is a circle, centre O. The tangent to the circle at the point P(2,-4) is shown.
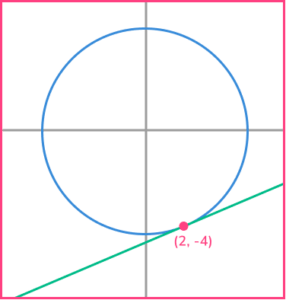
Find an equation of the tangent at the point P.
(3 marks)
Gradient of radius =\cfrac{-4}{2}=-2
(1)
Gradient of tangent =\cfrac{1}{2}
(1)
Equation of tangent is y=\cfrac{1}{2} x-5 \ or \ 2x-4y=20
(1)
2. The line l is a tangent to the circle x^{2}+y^{2}=18 at the point A.
A is the point (3,3).
The line l crosses the x -axis at point B.
Work out the area of triangle OAB.
(5 marks)
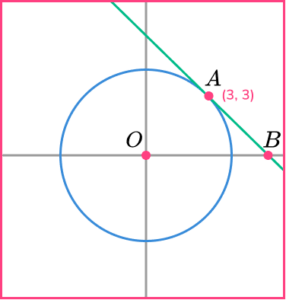
Gradient of radius =\cfrac{3}{3}=1
(1)
Gradient of tangent =-1
(1)
Equation of tangent is x+y=6, or finding c=6
(1)
x -coordinate of B is 6
(1)
Area of triangle =\cfrac{6 \times 3}{2}=9 (square units)
(1)
3. Prove algebraically that the straight line with equation 3y-x=30 is a tangent to the circle with equation x^{2}+y^{2}=90.
(5 marks)
Rearrange 3y-x=30 \ to \ x=3y-30 and substitute into x^{2}+y^{2}=90.
(1)
(3y-30)^{2}=9 y^{2}-180 y+900(1)
Simplify the equation of the circle to
10 y^{2}-180 y+810=0 \Rightarrow y^{2}-18 y+81=0.(1)
Solve to get y=9.
(1)
Statement: There is only one point of intersection so the line is a tangent to the circle.
(1)
Learning checklist
You have now learned how to:
- Find the equation of the tangent to a circle at a given point
- Find the x -coordinate of the point where the tangent intersects the x -axis
- Prove algebraically that a given line is a tangent to a given circle
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.