One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

Learn more

In order to access this I need to be confident with:

Parts of a circle Calculator skills Units of measurement Squares and square roots

This topic is relevant for:

GCSE Maths Geometry and Measure 2D Shapes Circles, Sectors & Arcs Parts Of A Circle

Area & Circumference Of A Circle

Area And Circumference Of A Circle

Here we will learn about calculating the area and circumference of a circle.

There are also area and circumference of a circle worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is the area and circumference of a circle?

The area of a circle is the amount of space within a circle and the circumference of a circle is the distance around the edge of the circle.

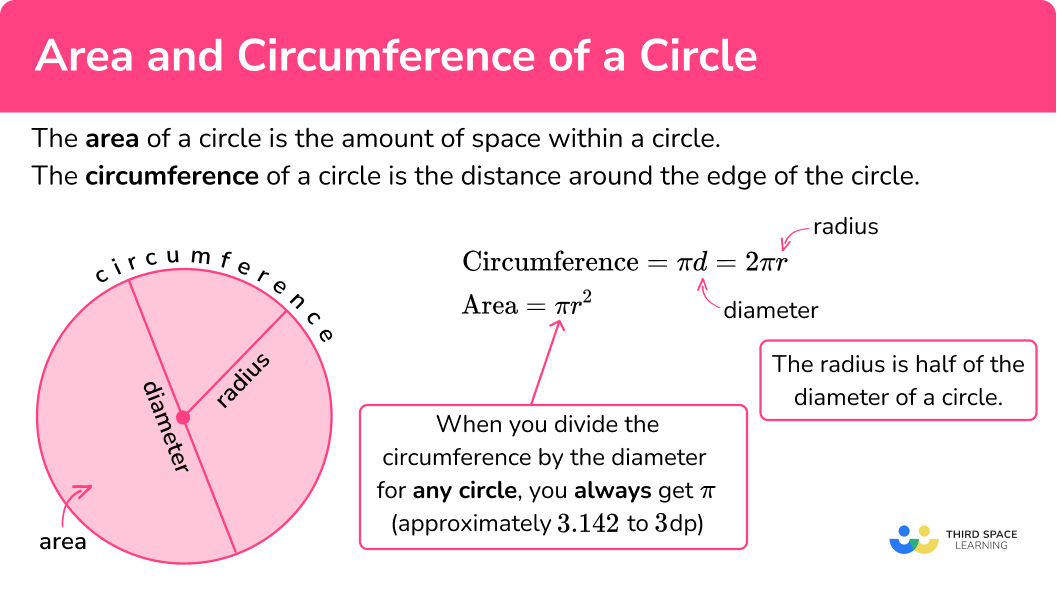
To calculate the area and circumference of a circle we use the following circle formulae,

\text{Area }= \pi r^{2}

\text{Circumference }= \pi d = 2\pi r

where $r$ is the radius of the circle (the distance from the centre of the circle to the edge) and $d$ is the diameter of the circle (the distance across the circle passing through the centre of the circle).

The symbol $\pi$ is the Greek letter “pi” where the value of pi is $3.14159265358979\dots$

As $\pi$ is an irrational number, the approximate value of $\pi$ is $3.142 \ (3dp).$

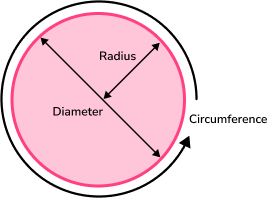
Area And Circumference Of A Circle image 1

The circumference of the circle is the perimeter of the circle and is proportional to its radius; as the radius increases, the circumference increases.

The circumference is a length and so it is measured using units such as $mm, \ cm, \ m.$

Area is measured in square units, such as $mm^2, \ cm^2$ or $m^2.$

What is the area and circumference of a circle?

How to calculate the area or circumference of a circle

In order to calculate the area or circumference of a circle:

Find the radius or diameter of the circle.
Use the relevant formula.
Give your answer clearly with the correct units.

Explain how to calculate the area or circumference of a circle

Area and circumference of a circle worksheet

Get your free area and circumference of a circle worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Area and circumference of a circle worksheet

Get your free area and circumference of a circle worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Area and circumference of a circle is part of our series of lessons to support revision on parts of a circle and circles, sectors and arcs. You may find it helpful to start with the main circles, sectors and arcs lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Area and circumference of a circle examples

Example 1: area of a circle given the radius

Find the area of this circle. Give your answer to $1$ decimal place.

Area And Circumference Of A Circle example 1

Find the radius or diameter of the circle.

To find the area, we need to know the radius. The radius of this circle is $9 \ cm.$

2Use the relevant formula.

The circle formula for area is $A= \pi r^{2}.$

\begin{aligned} A&= \pi r^{2}\\\\ A&= \pi \times 9^{2}\\\\ &=254.4690049 \end{aligned}

3Give your answer clearly with the correct units.

We need to give our answer to $1$ decimal place. Since the radius is measured in cm, the area will be measured in $cm^2.$

\text{Area }=254.5cm^{2}\text{ (1dp)}

Example 2: area of a circle given the diameter

Find the area of this circle. Give your answer in terms of $\pi .$

Area And Circumference Of A Circle example 2

Find the radius or diameter of the circle.

To find the area, we need to know the radius. The diameter of this circle is $6 \ mm$ and therefore the radius is $3 \ mm.$

Use the relevant formula.

The formula for area is $A= \pi r^{2}.$

$\begin{aligned} A&= \pi r^{2}\\\\ A&= \pi \times 3^{2}\\\\ &=9 \pi \end{aligned}$

Give your answer clearly with the correct units.

Here we are asked to give our answer in terms of pi $(\pi).$ The diameter is measured in $mm$ so the area will be measured in $mm^2.$

$\text{Area }= 9 \pi \ {mm}^{2}$

Example 3: circumference of a circle given the radius

Find the circumference of this circle. Give your answer to $3$ significant figures.

Area And Circumference Of A Circle example 3

Find the radius or diameter of the circle.

To find the circumference we can use the radius or the diameter. The radius of this circle is $21 \ m.$

Use the relevant formula.

To find the circumference using the radius we can use the formula $C=2 \pi r.$

$\begin{aligned} C&=2 \pi r\\\\ C&=2 \times \pi \times 21\\\\ & =131.9468915 \end{aligned}$

Give your answer clearly with the correct units.

Here we are asked to give our answer to $3$ significant figures. The radius is measured in $m$ so the circumference will also be measured in $m.$

$\text{Circumference }=132m\text{ (3sf)}$

Example 4: circumference of a circle given the diameter

Find the circumference of this circle. Give your answer in terms of $\pi .$

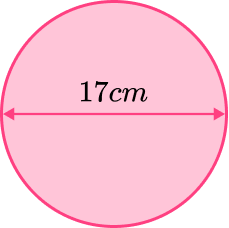
Area And Circumference Of A Circle example 4

Find the radius or diameter of the circle.

To find the circumference we can use the radius or the diameter. The diameter of this circle is $17 \ cm.$

Use the relevant formula.

To find the circumference using the diameter we can use the formula $C= \pi d.$

$\begin{aligned} C&= \pi d\\\\ C&=\pi \times 17\\\\ &=17 \pi \end{aligned}$

Give your answer clearly with the correct units.

Here we are asked to give the answer in terms of $\pi.$ The diameter is measured in $cm$ so the circumference will also be measured in $cm.$

$\text{Circumference }=17 \pi ~ \mathrm{cm}$

Example 5: area of a semicircle

Find the area of this semicircle. Give your answer to $2$ decimal places.

Area And Circumference Of A Circle example 5

Find the radius or diameter of the circle.

From the diagram of the semicircle, we can see that the diameter of the circle is $10 \ cm.$ For area we need the radius which is $10 \div 2=5 \ cm.$

Use the relevant formula.

To find the area of a semicircle, we find the area of the whole circle and half it.

$\begin{aligned} A&=\pi{r}^{2}\div{2}\\\\ &=\pi\times{5}^{2}\div{2}\\\\ &=25\pi\div{2}\\\\ &=12.5\pi\\\\ &=39.26990817 \end{aligned}$

Give your answer clearly with the correct units.

We have been asked to give the answer to $2$ decimal places. The diameter is measured in $cm$ therefore the area will be measured in $cm^2.$

$\text{Area }=39.27 \ cm^{2}\text{ (2dp)}$

Example 6: circumference of a circle given the area

The area of a circle is $30 \ cm^2.$ Work out the circumference of the circle. Give your answer to $3$ significant figures.

Find the radius or diameter of the circle.

In this case we are given the area of the circle and we need to work backwards to find the radius. Substituting the values we know into the area formula we get,

$\begin{aligned} \text{Area }&= \pi r^{2}\\\\ 30&= \pi r^{2} \end{aligned}$

We can then solve this to find $r.$

$30=\pi{r}^{2}$

Dividing both sides by $\pi,$ we get

$\frac{30}{\pi}=r^{2}.$

As we have $r^2,$ we need to square root both sides to get $r$ on its own.

$\sqrt{\frac{30}{\pi}}=r$

Evaluating this, we have $r=3.090193616.$

It is important not to round this value yet as this will cause us to lose accuracy in our final answer.

Use the relevant formula.

Now that we have the radius we can use the relevant formula to find the circumference.

$\begin{aligned} C&=2 \pi r\\\\ &=2 \times \pi \times 3.090193616\\\\ &=19.41625913 \end{aligned}$

Give your answer clearly with the correct units.

We have been asked to give the answer to $3$ significant figures. The area is measured in $cm^2$ so the circumference will be measured in $cm.$

$\text{Circumference }=19.4 \ cm \ (3sf)$

Common misconceptions

Incorrectly using the radius or diameter of a circle

It is important to know the difference between the diameter and the radius of a circle and to use the correct one in the calculation.

Using an incorrect formula

It can be easy to get confused between the different formulae – make sure you know which formula is for which calculation.

Incorrect use of BIDMAS

When calculating the area of a circle, we need to calculate the square of the radius first as the radius is raised to the power of $2,$ and then multiply this value by $\pi .$ This is because indices come before multiplication in BIDMAS.

For example, for a circle with radius $4 \ cm,$

$A=\pi\times{4}^{2}=\pi\times{16}=50.26548246…$ (Correct)

$A=(\pi\times{4})^{2}=\pi^{2}\times{16}=157.9136704…$ (Incorrect)

Not including the correct units

Remember that circumference is a measure of length, such as $mm, \ cm$ or $m$ and area is measured in square units, such as $mm^2, \ cm^2$ or $m^2.$

Not rounding correctly

Read the question again at the end to ensure you have given the answer to the correct degree of accuracy and always ensure you apply the rules of rounding when rounding an answer.

Practice area and circumference of a circle questions

69.1 \ cm^2

1520.5 \ cm^2

34.6 \ cm^2

380.1 \ cm^2

The radius of the circle is $11 \ cm.$

\begin{aligned} \text{Area }&=\pi r^{2}\\\\ &=\pi \times 11^{2}\\\\ &=380.1327111 \\\\ &=380.1 \mathrm{cm}^{2}~\text{(1dp)} \end{aligned}

49 \pi \ \mathrm{mm}^{2}

14 \pi \ \mathrm{mm}^{2}

28 \pi \ \mathrm{mm}^{2}

196 \pi \ \mathrm{mm}^{2}

The diameter is $14 \ mm$ so the radius is $7 \ mm.$

\begin{aligned} \text{Area }&= \pi r^{2}\\\\ &= \pi \times 7^{2}\\\\ &=49 \pi ~ \mathrm{mm}^{2} \end{aligned}

2.51 \ m

2.01 \ m

5.03 \ m

8.04 \ m

The radius of the circle is $0.8m.$

\begin{aligned} \text{Circumference }&=2 \pi r\\\\ &= 2 \times \pi \times 0.8\\\\ &=5.026548246\\\\ &=5.03 \ \mathrm{m} ~ \text{(3sf)} \end{aligned}

26 \pi ~\mathrm{cm}

13 \pi ~\mathrm{cm}

169 \pi ~\mathrm{cm}

676 \pi ~\mathrm{cm}

The diameter of the circle is $26m.$

\begin{aligned} \text{Circumference}&=\pi d\\\\ &=\pi \times 26\\\\ &=26 \pi~\mathrm{cm} \end{aligned}

1020 \ cm^2

254 \ cm^2

28.3 \ cm^2

63.3 \ cm^2

Here we want to find the area of $\frac{1}{4}$ of a circle. We can see from the diagram that the radius of the circle is $18 \ cm.$ We can find the area of the whole circle and then divide by $4.$

\begin{aligned} \text{Area of whole circle }&=\pi r^{2}\\\\ &=\pi \times 18^{2}\\\\ &=324\pi \\ \end{aligned}

\begin{aligned} \text{Area of quarter circle }= 324\pi \div 4 &= 81\pi\\\\ &=254.4690049\\\\ &=254\mathrm{cm}^{2}~\text{(3sf)} \end{aligned}

1963.50 \ cm^2

15.92 \ cm^2

795.77 \ cm^2

198.94 \ cm^2

\begin{aligned} \text{Circumference }&=\pi d\\\\ 50&=\pi d\\\\ \frac{50}{\pi}&=d\\\\ d&=15.91549431 \end{aligned}

\begin{aligned} r&=15.91549431 \div 2\\\\ &=7.957747155 \end{aligned}

\begin{aligned} \text{Area }&=\pi r^{2}\\\\ &=\pi \times 7.957747155^{2}\\\\ &=198.9436789\\\\ &=198.94 \ \mathrm{cm}^{2} \ (2dp) \end{aligned}

Area and circumference of a circle GCSE questions

1. Josh is calculating the circumference of this circle.

Area And Circumference Of A Circle GCSE question 1

Here is Josh’s working.

\begin{aligned} 2 \times \pi \times 22 &=138.2300768\\\\ &=138.2 \ \mathrm{cm}~\text{(1pd)} \end{aligned}

What mistake has Josh made?

(1 mark)

Show answer

He has used the diameter $(22 \ cm)$ instead of the radius $(11 \ cm)$ in $C=2 \pi r.$

(1)

2. (a) Vicky has a garden with a circular pond, as shown below.

Area And Circumference Of A Circle GCSE question 2

Calculate the area of the pond. Give your answer to $3$ significant figures.

(b) Vicky wants to buy grass seed to cover the lawn.

Grass seed comes in boxes which cover $20 \ m^2$ per box.

Vicky has $5$ boxes of seed. Does she have enough to cover her lawn?

(5 marks)

Show answer

(a)

Radius $=2.5 \ m$

(1)

\text{Area }=\pi \times 2.5^{2}=19.6 \ \mathrm{m}^{2}

(1)

(b)

Area of the garden is $8 \times 14=112 \ \mathrm{m}^{2}$ .

(1)

Area of the lawn is $112-19.6=92.4 \ \mathrm{m}^{2}$ .

(1)

$92.4 \div 20=4.62$ boxes required. Yes she does.

(1)

3. Here are two pizzas sold in a restaurant. Which pizza is better value for money?

Area And Circumference Of A Circle GCSE question 3

(5 marks)

Show answer

Area of the large pizza is $\pi \times 18^{2}=1017.876 \ \mathrm{cm}^{2}$ .

(1)

$1017.876 \div 12 = 84.82 \ \mathrm{cm}^{2}$ per $£1$ .

(1)

Area of the small pizza is $\pi\times 14^{2}=615.752 \ \mathrm{cm}^{2}$ .

(1)

$615.75 \div 8=76.97 \ \mathrm{cm}^{2}$ per $£1$ .

(1)

Large pizza is better value.

(1)

Learning checklist

You have now learned how to:

Calculate the area of a circle

Calculate the circumference of a circle

Solve problems involving area and circumference of a circle

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.