Circle Theorems

Here we will learn about circle theorems, including their application, proof, and how to use them to solve more difficult problems.

There are also circle theorem worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What are circle theorems?

Circle theorems are properties that show relationships between angles within the geometry of a circle. We can use these theorems along with prior knowledge of other angle properties to calculate missing angles, without the use of a protractor. This has very useful applications within design and engineering.

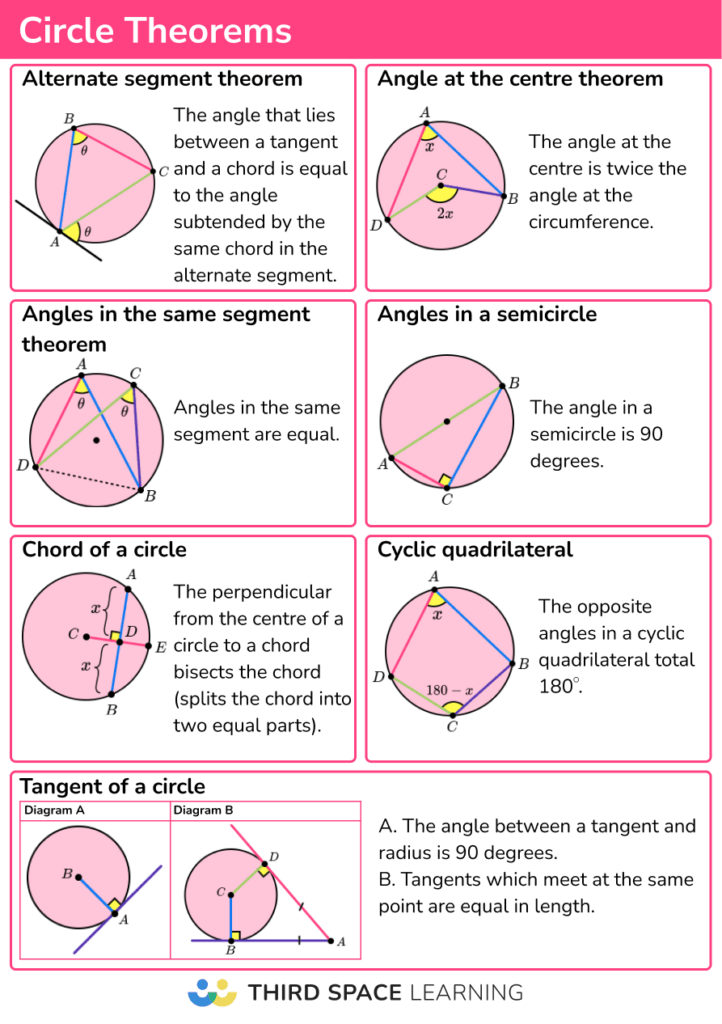
There are seven main circle theorems:

1. Alternate segment circle theorem
2. Angle at the centre circle theorem
3. Angles in the same segment circle theorem
4. Angle in a semi circle theorem
5. Chord circle theorem
6. Tangent circle theorem
7. Cyclic quadrilateral circle theorem

Below is a summary of each circle theorem, along with a diagram. You need to remember all of these circle theorem rules and be able to describe each one in a sentence.

What are circle theorems?

Download our free circle theorems poster to focus your revision!

Circle Theorem 1: The alternate segment

The angle that lies between a tangent and a chord is equal to the angle subtended by the same chord in the alternate segment.

Step-by-step guide: Alternate segment theorem

How to use the alternate segment theorem

To use the alternate segment theorem

1. Locate the key parts of the circle for the theorem.
2. Use other angle facts to determine one of the two angles.
3. Use the alternate segment theorem to state the other missing angle.

Circle Theorem 2: Angles at the centre and at the circumference

The angle at the centre is twice the angle at the circumference.

Step-by-step guide: Angle at the centre is twice the angle at the circumference

How to use the angle at the centre theorem

To use the fact that the angle at the centre is twice the angle at the circumference

1. Locate the key parts of the circle for the theorem.
2. Use other angle facts to determine the angle at the centre or the angle at the circumference.
3. Use the angle at the centre theorem to state the other missing angle.

Circle Theorem 3: Angles in the same segment

Angles in the same segment are equal.

Step-by-step guide: Angles in the same segment are equal

How to use the angles in the same segment theorem

To use the fact that angles in the same segment are equal

1. Locate the key parts of the circle for the theorem.
2. Use other angle facts to determine an angle at the circumference in the same segment.
3. Use the angle in the same segment theorem to state the other missing angle.

Circle Theorem 4: Angles in a semicircle

The angle in a semicircle is 90 degrees.

Step-by-step guide: Angle in a semicircle

How to use the angles in a semicircle theorem

To use the fact that angles in a semicircle equal 90^o

1. Locate the key parts of the circle for the theorem.
2. Use other angle facts to determine angles within the triangle.
3. Use the angles in a semicircle theorem to state the other missing angle.

Circle Theorem 5: Chord of a circle

The perpendicular from the centre of a circle to a chord bisects the chord (splits the chord into two equal parts).

Step-by-step guide: Chord of a circle

How to find missing lengths using chords

To find missing angles and lengths using chords

1. Locate the key parts of the circle for an appropriate circle theorem.
2. Use other angle facts to determine any missing angles.
3. Use Pythagoras’ theorem or trigonometry to find the missing length.

Circle Theorem 6: Tangent of a circle

The angle between a tangent and radius is 90 degrees. Tangents which meet at the same point are equal in length.

Diagram 1                      Diagram 2

Step-by-step guide: Tangent of a circle

How to use the tangent of a circle theorems

To use the tangent of a circle:

1. Locate the key parts of the circle for the theorem.
2. Use other angle facts to determine the remaining angle(s) made with the tangent.
3. Use the tangent theorem to state the other missing angle.

Circle Theorem 7: Cyclic quadrilateral

The opposite angles in a cyclic quadrilateral total 180^o .

Step-by-step guide: Cyclic quadrilateral

How to use the cyclic quadrilateral theorem

To use the cyclic quadrilateral theorem

1. Locate the key parts of the circle for the theorem.
2. Use other angle facts to determine one of the two opposing angles in the quadrilateral.
3. Use the cyclic quadrilateral theorem to state the other missing angle.

Subtended angles

An angle within a circle is created by two chords meeting at a point on the circumference. The diagrams below show the angle subtended by arc AC from point B for two different circles.

Top tip: The word subtend is used a lot within circle theorems so make sure you know what it means.

Step-by-step guide: Subtended angles

Circle theorems examples

Example 1: the alternate segment theorem

The triangle ABC is inscribed in a circle with centre O. The tangent DE meets the circle at the point A. Calculate the size of the angle ABC.

1. Locate the key parts of the circle for the theorem

Here we have:

• The tangent DE
• The chord AC (that meets the tangent)
• The angle CAE = 56^o
• The angle ABC = \theta

2Use other angle facts to determine one of the two angles

We already know that CAE = 56^o so we do not need to use any other angle fact to determine this angle for this example.

3Use the alternate segment theorem to state the other missing angle

ABC = 56^o as angles in the alternate segment are equal to the angle between the tangent and the associated chord.

Example 2: angles at the centre theorem

ABCD is an arrowhead where C is the centre of the circle and A, B, and D lie on the circumference. Calculate the size of angle BAD.

Locate the key parts of the circle for the theorem

Here we have:

• The angle BCD = 150^o
• BC = CD = Radii
• AB and AD are chords
• The angle BAD = \theta

Example 3: angles in the same segment theorem

Below is a circle with centre O. AC and BD are chords. Calculate the size of angle CAD.

Locate the key parts of the circle for the theorem

Here we have:

• The angle CBD = 47^o
• AC and BD are chords
• The angle CAD = \theta

Example 4: angles in a semicircle theorem

ABC is a triangle where A, B, and C lie on the circumference and AB is a diameter. Angle ABC is 67^o . Calculate the size of angle BAC.

Locate the key parts of the circle for the theorem

Here we have:

• The angle ABC = 67^o
• AB is a diameter
• AC and BC are chords
• The angle CAB = \theta

Example 5: chord of a circle (cosine ratio)

Below is a circle with centre C. Points A, B, C, and D are on the circumference of the circle. The chord AB is perpendicular to the line CD at the point E. The line AE is 5cm and angle ADE = 71^o . Calculate the length of the line BC correct to 1 decimal place.

Locate the key parts of the circle for an appropriate circle theorem

Here we have:

• CD is a diameter
• AB is a chord, perpendicular to CD
• The angle ADE = 71^o
• The angle BEC = 90^o Radii
• The line AE = 5cm
• The line BC = x

Use other angle facts to determine other necessary angles

As angles in the same segment are equal, angle ADE is equal to angle ABC so angle ABC = 71^o . Also, as the perpendicular from the centre of a circle to a chord bisects the chord, the line BE is equal to AE, so BE = 5cm .

Example 6: tangent of a circle theorem

Points A, B, and C are on the circumference of a circle with centre O. DE is a tangent at point A. Calculate the size of angle BAD.

Locate the key parts of the circle for the theorem

Here we have:

• The angle BCA = 52^o
• AC is a diameter
• DE is a tangent
• The angle BAD = \theta

Use other angle facts to determine the remaining angle(s) made with the tangent

As AC is a diameter and the angle in a semicircle is 90^o , angle ABC = 90^o . As angles in a triangle total 180^o ,

\begin{aligned} &CAB=180-(90+52)\\\\ &CAB=38^o \end{aligned}

Example 7: cyclic quadrilateral

ABCD is a quadrilateral where A, B, C and D lie on the circumference of a circle. Calculate the size of angle BCD.

Locate the key parts of the circle for the theorem

Here we have:

• The angle BAD = 51^o
• The angle BCD = \theta

Common misconceptions

Below are some of the common misconceptions for all of the circle theorems:

• Add to 90/180/360 degrees

Make sure you know the other angle facts including:

Angles on a straight line total 180^o

Angles at a point total 360^o

Angles in a triangle total 180^o

Angles in a quadrilateral total 360^o

• Halving and doubling

By remembering the angle at the centre theorem incorrectly, the student will double the angle at the centre, or half the angle at the circumference.

Top tip: look at the angles. The angle at the centre is always larger than the angle at the circumference (this isn’t so obvious when the angle at the circumference is in the opposite segment).

• Angles are the same

Make sure that you know when two angles are equal. Look out for isosceles triangles and the angles in the same segment.

• Cyclic quadrilateral

The angles that are either end of the diameter total 180^o as if the triangle were a cyclic quadrilateral. They should total 90^o as the angle in a semicircle is 90^o .

• A diameter or a chord?

The angle at the circumference is assumed to be 90^o when the associated chord does not intersect the centre of the circle and so the diagram does not show a semicircle.

• Parallel lines (alternate segment theorem)

Take for example the diagram below:

The chord BC is assumed to be parallel to the tangent and so the angle ABC is equal to the angle at the tangent. Here the angle BCA would be equal.

Top tip: Use arrows to visualise which way the alternate segment angle appears:

• Opposite angles in a cyclic quadrilateral

The angle is taken from 180^o which is a confusion with opposite angles in a cyclic quadrilateral.

Here, angle ABC is incorrectly calculated as 180 - 56 = 124^o .

The angle ABC = 56^o as it is in the alternate segment to the angle CAE.

• Angle at the centre is supplementary to opposing angle

As the shape is a quadrilateral, the angle at the centre is assumed to be supplementary and add to 180^o .

• Opposite angles are the same for a cyclic quadrilateral

As angles in the same segment are equal, the opposing angles in a quadrilateral are assumed to be equal. The only case of this is when both angles are 90^o .

• Pythagoras’ theorem missing side

The missing side is calculated by incorrectly adding the square of the hypotenuse and a shorter side, or subtracting the square of the shorter sides.

• Incorrect trigonometric function

The incorrect trigonometric function is used and so the side or angle being calculated is incorrect. This also includes the inverse trigonometric functions.

• Incorrect assumption of isosceles triangles

The intersection of the diameter and the chord at 90 degrees can be very close to the centre and so the two lengths coming from the point of intersection to the radius are assumed to be equal, but they aren’t.

The next lessons are

• Circles, sectors and arcs
• Equation of a circle
• Circumference of a circle

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.