GCSE Tutoring Programme
Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.
In order to access this I need to be confident with:
Fractions Decimals 2D shapes Coordinates maths Arithmetic Negative numbers Scale drawingThis topic is relevant for:

Scale Factor
Here we will learn about scale factor, including enlarging a shape by a scale factor on a grid. We will extend this to learn about fractional scale factors and how to calculate scale factors.
There are also worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is a scale factor?
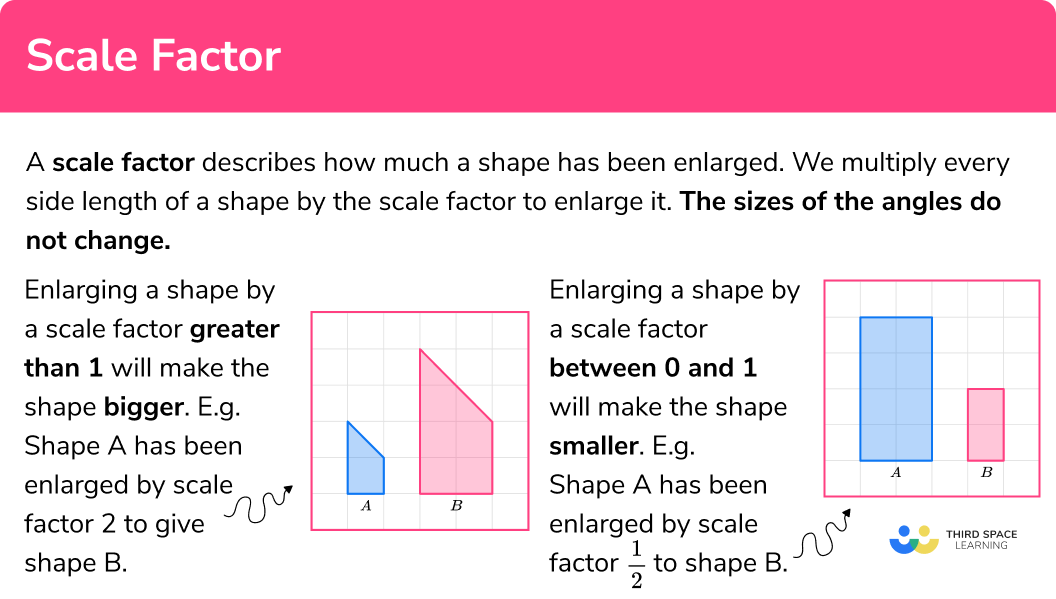
A scale factor describes how much a shape has been enlarged.
We multiply every side length of a shape by the scale factor to enlarge it. The sizes of the angles do not change.
- Enlarging a shape by a scale factor greater than 1 will make the shape bigger.
E.g.
Shape A has been enlarged by scale factor 2 to give shape B .
The corresponding angles are identical but each side in shape B is double the size of the original shape. The corresponding angles are identical.
The two shapes are similar shapes.
- Enlarging a shape by a scale factor between 0 and 1 will make the shape smaller. This is often written as a fraction and is known as a fractional scale factor.
E.g.
Shape A has been enlarged by scale factor \frac{1}{2} to shape B .
If you look at the corresponding sides, each side in shape B is half the size of the original shape. The corresponding angles are identical.
The two shapes are similar shapes.
What is a scale factor?
How to use a scale factor
In order to use a scale factor to enlarge a shape:
- Draw an enlargement of the first side.
- Enlarge another side.
- Complete the enlarged shape.
How to use a scale factor

Scale factor worksheet

Get your free scale factor worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Scale factor worksheet

Get your free scale factor worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREEScale factor examples
Example 1: use a scale factor to enlarge a shape
Enlarge this shape by scale factor 2 :
- Draw an enlargement of the first side.
Let’s start with the base. The base in the original shape is 1 , so the base in the enlarged shape will be 2 .
1\times2=2You can draw it anywhere on the grid.
2Enlarge another side.
Let’s choose a side that is attached to the first side. The height of the first shape is 3 , so the height of the enlarged shape will be 6 .
3\times2=63Complete the enlarged shape.
Now continue to draw the new shape.
The lengths of the sides of the second shape are double the lengths of the original shape.
Example 2: use a scale factor to enlarge a shape
Enlarge this shape by scale factor 3 :
The base in the original shape is 2 , so the base in the enlarged shape will be 6 .
2\times3=6You can draw it anywhere on the grid.
The left vertical side of the first shape is 3 , so the corresponding side of the enlarged shape will be 9 .
3\times3=9Now continue to draw the new shape. It is easier to do the horizontal and vertical sides first.
The lengths of the sides of the second shape are three-times the lengths of the original shape.
Example 3: use a scale factor to enlarge a shape
Enlarge this shape by scale factor \frac{1}{2} :
The base in the original shape is 4 , so the base in the enlarged shape will be 2 .
4\times \frac{1}{2}=2You can draw it anywhere on the grid.
The left vertical side of the first shape is 2 , so the corresponding side of the enlarged shape will be 1 .
2\times \frac{1}{2}=1Now continue to draw the new shape. It is easier to do the horizontal and vertical sides first.
The lengths of the sides of the second shape are half the lengths of the original shape.
How to calculate a scale factor
In order to calculate a scale factor:
- Choose a pair of corresponding sides.
- Divide the length of the enlarged shape by the length of the original shape.
- Write down the scale factor.
How to calculate a scale factor

Calculating a scale factor examples
Example 4: calculating a scale factor
Calculate the scale factor for the enlargement of Triangle A to Triangle B :
The two triangles are similar triangles.
Choose a pair of sides, either horizontal or vertical. Here I am choosing the bases.
The base of shape A is 3 .
The base of shape B is 9 .
We need to divide the enlarged length by the original length.
Scale \ factor = \frac{enlarged \ length}{ original \ length}=\frac{9}{3}=3The scale factor of enlargement for Triangle A to Triangle B is 3 .
Example 5: calculating a scale factor
Calculate the scale factor for the enlargement of Shape A to Shape B :
Let’s choose the vertical sides on the left.
The length of shape A is 2 .
The length of shape B is 4 .
We need to divide the enlarged length by the original length.
Scale \ factor = \frac{enlarged \ length}{ original \ length}=\frac{4}{2}=2The scale factor of enlargement for shape A to shape B is 2 .
Example 6: calculating a scale factor
Calculate the scale factor for the enlargement of Shape A to Shape B :
Let’s choose the bases.
The length of shape A is 9 .
The base of shape B is 3 .
We need to divide the enlarged length by the original length.
Scale \ factor = \frac{enlarged \ length}{ original \ length}=\frac{3}{9}=\frac{1}{3}The scale factor of enlargement for shape A to shape B is \frac{1}{3} .
Common misconceptions
- Fractional scale factors and enlargement
When we are asked to enlarge a shape by a fractional scale factor such as \frac{1}{2} , the shape becomes smaller.
- Diagonal lines
Diagonal lines can be tricky to enlarge, so it is best to use horizontal and vertical lines. In this kite a horizontal and a vertical line are added to make the enlargement by scale factor 2 easier.
- Areas of enlarged shapes
E.g.
For these squares the scale factor of enlargement is 2 . All the lengths have doubled. The perimeter is doubled.
But the area of the second shape is 4 times larger than the area of the first shape.
For more information on this, check out our lesson on similar shapes.
Step-by-step guide: Similar shapes
Related lessons
Scale factor is part of our series of lessons to support revision on enlargement. You may find it helpful to start with the main enlargement lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Practice scale factor questions
1. Enlarge this shape by scale factor 2




The original shape is a rectangle. The base of the original shape is 2 , so the base of the enlarged shape will be 4 .
2 \times 2=4
The height of the original shape is 1 , so the height of the enlarged shape will be 2 .
1 \times 2=2
The enlargement will be a rectangle with base 4 and height 2 .
2. Enlarge this shape by scale factor 4




The original shape is a square, so will the enlarged shape. The side of the original square is 1 , so the side of the enlarged square will be 4 .
1 \times 4=4
The enlargement will be a square with side length 4 .
3. Enlarge this shape by scale factor \frac{1}{2}




The original shape has a base of 6 , so the base of the enlarged shape will be 3 .
6 \times \frac{1}{2}=3
The other sides need to be halved too.
4. Calculate the scale factor of the enlargement from shape A to shape B .
Scale factor \frac{1}{4}

Scale factor \frac{1}{2}

Scale factor 4

Scale factor 2

The original shape has a base of 2 .
The base of the enlarged shape is 4 .
Scale \ factor = \frac{enlarged \ length}{ original \ length}=\frac{4}{2}=25. Calculate the scale factor of the enlargement from shape A to shape B .
Scale factor \frac{1}{3}

Scale factor 2

Scale factor 3

Scale factor \frac{1}{2}

The original shape has a base of 6 .
The base of the enlarged shape is 2 .
Scale \ factor = \frac{enlarged \ length}{ original \ length}=\frac{6}{2}=3
6. Calculate the scale factor of the enlargement from shape A to shape B .
Scale factor \frac{1}{3}

Scale factor 2

Scale factor \frac{1}{2}

Scale factor 3

The two triangles need to be similar triangles.
The original shape has a vertical height of 6 .
The vertical height of the enlarged shape is 3 .
Scale \ factor = \frac{enlarged \ length}{ original \ length}=\frac{3}{6}=\frac{1}{2}
Scale factor GCSE questions
1. On the grid, draw an enlargement of the rectangle with scale factor 3 .
(2 marks)
For 2 sides correctly enlarged
(1)
For all 4 sides correctly enlarged
(1)
2. On the grid, draw an enlargement of the rectangle with scale factor 2 .
(2 marks)
For 2 sides correctly enlarged
(1)
For all 4 sides correctly enlarged
(1)
3. The shaded shape has been enlarged by scale factor \frac{1}{2} ? Which is the correct enlargement?
Circle your answer A B C D
(1 mark)
Shape C
(Correct answer only)
(1)
Learning checklist
You have now learned how to:
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.