One to one maths interventions built for KS4 success
Weekly online one to one GCSE maths revision lessons now available
This topic is relevant for:

Centre Of Enlargement
Here we will learn about the centre of enlargement, including how to enlarge a shape about a point. We will also learn about fractional scale factors and negative scale factors.
There are also enlargement worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.
What is centre of enlargement?
Centre of enlargement is a point which tells you where to draw an enlargement.
An enlargement is a type of transformation where we change the size of the original shape to make it bigger or smaller by multiplying it by a scale factor.
To use a centre of enlargement we need to draw lines from the centre of enlargement through the vertices of the original shape. These are called ray lines.
E.g.
Here triangle ABC has been enlarged by scale factor 2 about a centre of enlargement point O.
The new triangle is labelled A’B’C’.
The lengths of the sides of the new shape are double the lengths of the sides of the original shape. The pairs of corresponding sides are parallel lines. The angles in the two shapes are the same and the triangles are similar triangles.
E.g.
Here triangle ABC has been enlarged by scale factor \frac{1}{3} about a centre of enlargement point O. If an enlargement is between 0 and 1 the shape becomes smaller. The new triangle is labelled A’B’C’.
The lengths of the sides of the new shape are a third of the lengths of the sides of the original shape.
The pairs of corresponding sides are parallel lines.
The angles in the two shapes are the same and the triangles are similar triangles.
A transformation, such as an enlargement, is a type of mathematical mapping. So the term “maps” is often used in questions.
A mapping is a mathematical instruction and a transformation is a mathematical instruction which can be applied to a shape.
What is centre of enlargement?

Negative scale factors
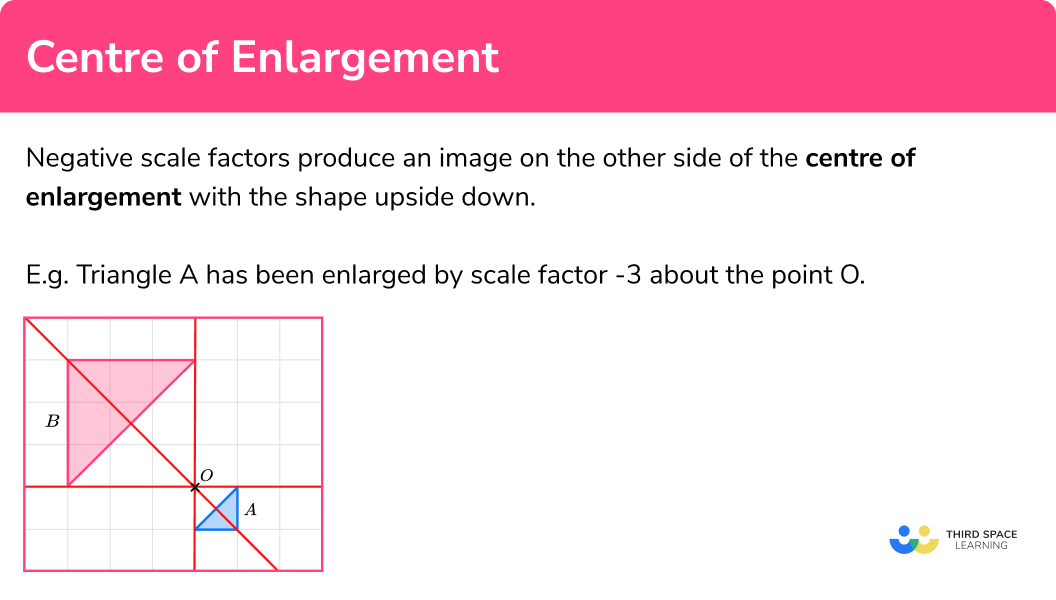
Negative scale factors produce an image on the other side of the centre of enlargement with the shape upside down.
Negative scale factors in the higher GCSE only. These are an extension of positive scale factors.
E.g.
Triangle A has been enlarged by scale factor -3 about the point O.
Negative scale factors
How to enlarge a shape using a centre of enlargement
In order to enlarge a shape using a centre of enlargement:
- Draw a ray line.
- Mark the new point.
- Mark the other new points.
- Complete the shape.
How to enlarge a shape using a centre of enlargement

Centre of enlargement worksheet

Get your free centre of enlargement worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREE
Centre of enlargement worksheet

Get your free centre of enlargement worksheet of 20+ questions and answers. Includes reasoning and applied questions.
DOWNLOAD FREECentre of enlargement examples
Example 1: on a grid
Enlarge the triangle ABC by scale factor 2 about the point O.
- Draw a ray line.
Choose a point to start with. Point A is a good place to start as it is across from the centre of enlargement, point O. Draw a ray line from point O through point A and extend the line.
2Mark the new point.
Measure the distance from point O to point A. Multiply the distance by the scale factor 2. Measure this new distance from point O and put a mark for the new point.
OA’=2\times OA3Mark the other new points.
Draw ray lines going through point B and point C. Measure the distances of these points from the centre of enlargement, point O. Multiply the distances by the scale factor 2. Measure these new distances from point O and put marks for the new points.
OB’=2\times OB OC’=2\times OC4Complete the shape.
Join up the points to make the new triangle A’B’C’.
Example 2: on a grid
Enlarge the triangle ABC by scale factor \frac{1}{2} about the point O.
Draw a ray line.
Choose a point to start with. Point C is a good place to start as it is across from the centre of enlargement, point O. Draw a ray line from point O through point C and extend the line.
Mark the new points.
Measure the distance from point O to point C. Multiply the distance by the scale factor \frac{1}{2} (or divide by 2 ). Measure this new distance from point O and put a mark for the new point.
OC’=\frac{1}{2}\times OC
Mark the other new points.
Draw ray lines going through point B and point C. Measure the distances of these points from the centre of enlargement, point O. Multiply the distances by the scale factor \frac{1}{2}. Measure these new distances from point O and put marks for the new points.
OA’=\frac{1}{2}\times OA
OB’=\frac{1}{2}\times OB
Complete the shape.
Join up the points to make the new triangle A’B’C’.
Example 3: on a coordinate grid
Enlarge the triangle ABC by scale factor 3 about the point P (8,8)
Mark the centre of enlargement.
On the diagram mark the centre of enlargement. The centre of enlargement is point P.
Draw a ray line.
Choose a point to start with. Point A is a good place to start as it is straight down from the centre of enlargement, point P. Draw a ray line from point P through point A and extend the line.
Mark the new point.
Measure the distance from point P to point A. Multiply the distance by the scale factor 3. Measure this new distance from point P and put a mark for the new point.
Mark the other new points.
Draw ray lines going through point B and point C. Measure the distances of these points from the centre of enlargement, point P. Multiply the distances by the scale factor 3. Measure these new distances from point P and put marks for the new points.
Complete the shape.
Join up the points to make the new triangle A’B’C’.
Example 4: on a coordinate grid
Enlarge the triangle ABC by scale factor \frac{1}{2} about O.
Mark the centre of enlargement.
On the diagram mark the centre of enlargement. The centre of enlargement is point O, the origin.
Draw a ray line.
Choose a point to start with. Point A is a good place to start as it is straight up from the centre of enlargement, point O. Draw a ray line from point O through point A and extend the line.
Mark the new point.
Measure the distance from point O to point A. Multiply the distance by the scale factor \frac{1}{2}. Measure this new distance from point O and put a mark for the new point.
Mark the other new points.
Draw ray lines going through point B and point C. Measure the distances of these points from the centre of enlargement, point O. Multiply the distances by the scale factor \frac{1}{2}. Measure these new distances from point O and put marks for the new points.
Complete the shape.
Join up the points to make the new triangle A’B’C’.
How to find a centre of enlargement
In order to find a centre of enlargement:
- Draw a ray line through a pair of points.
- Draw more ray lines.
- Write down the coordinates of the centre of enlargement.
Example 5: find a centre of enlargement
Triangle A has been enlarged to make triangle B.
Find the centre of enlargement.
Draw a ray line through a pair of points.
Find a pair of corresponding vertices and draw a ray line going through the points.
Draw more ray lines.
Find more pairs of corresponding vertices. Draw ray lines through the pairs of points.
Write down the coordinates of the centre of enlargement.
The point at which your ray lines meet will be the centre of enlargement.
The centre of enlargement is (2,2)
You may also be asked to find the scale factor of enlargement. For this example the scale factor of enlargement is 2. You can calculate the scale factor by choosing a pair of corresponding sides and dividing the enlarged length by the original length.
Example 6: find a centre of enlargement
Triangle A has been enlarged to make triangle B.
Find the centre of enlargement.
Draw a ray line through a pair of points.
Find a pair of corresponding vertices and draw a ray line going through the points.
Draw more ray lines.
Find more pairs of corresponding vertices. Draw ray lines through the pairs of points
Write down the coordinates of the centre of enlargement.
The point at which your ray lines meet will be the centre of enlargement.
The centre of enlargement is (5,9)
How to enlarge a shape using a negative scale factor (higher)
In order to enlarge a shape using a centre of enlargement on a coordinate grid:
- Draw a ray line.
- Mark the new point.
- Mark the other new points.
- Complete the shape.
Example 7: negative scale factor
Enlarge the triangle ABC by scale factor -2 about the point O
Draw a ray line.
Choose a point to start with. Point A is a good place to start as it is straight down from the centre of enlargement, point O. Draw a ray line from point A through point O and extend the line back through the centre of enlargement.
Mark the new point.
Measure the distance from point O to point A. Multiply the distance by 2, but since the scale factor is negative 2 we mark the point A’ measuring backwards along the ray line from point O.
The ray line is like a number line where we have positive and negative numbers with 0 in between.
OA’=-2\times OA
Mark the other new points.
Draw ray lines going through point B and point C. Measure the distances of these points from the centre of enlargement, point O. Multiply the distance by 2 , but since the scale factor is negative 2 we mark the new points’ measuring backwards along the ray line from point O.
Complete the shape.
Join up the points to make the new triangle A’B’C’.
Example 8: negative scale factor
Enlarge the triangle ABC by scale factor -1 about the origin.
Draw a ray line.
The centre of enlargement is O, the origin. Choose a point to start with. Let’s choose point A. Draw a ray line from point A through O and extend the line back through the centre of enlargement.
Mark the new point.
Measure the distance from point O to point A. Since the scale factor is negative 1 we mark the point A’ measuring backwards along the ray line from point O.
The ray line is like a number line where we have positive and negative numbers with 0 in between.
OA’=-1\times OA
Mark the other new points.
Draw ray lines going through point B and point C. Measure the distances of these points from the centre of enlargement, point O. Since the scale factor is negative 1 we mark the new points measuring backwards along the ray line from point O.
Complete the shape.
Join up the points to make the new triangle A’B’C’.
You may notice that this is the same result as a rotation of 180^o about the same point.
Common misconceptions
- Accuracy
Use a sharp pencil and make use of the grid lines to help you to be accurate.
- Extend your ray lines
Remember that the ray lines can be extended as far as needed.
- Draw multiple ray lines
It is a good idea to draw at least 3 ray lines to make sure you find the correct centre of enlargement.
- Position of the centre of enlargement
Remember the centre of enlargement can be within the shape.
E.g.
- The origin
The origin of a coordinate grid has the coordinates (0,0) . It is commonly denoted as O. It is used often as the centre of enlargement.
- Objects and images
The original shape is known as an object. The enlarged shape is known as an image. They can overlap.
Related lessons
Centre of enlargement is part of our series of lessons to support revision on enlargement. You may find it helpful to start with the main enlargement lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:
Practice centre of enlargement questions
1. Enlarge this shape by scale factor 3 about the point O




Draw ray lines to make sure you get the enlarged triangle in the correct position. The sides of the enlarged triangle should be 3 times bigger than the original shape.
2. Enlarge this shape by scale factor 2 about the point O




Draw ray lines to make sure you get the enlarged triangle in the correct position. The scale factor is 2 , so each of the sides of the enlarged triangle should be double the sides of the original triangle.
3. Enlarge this shape by scale factor 3 about the point (5,1)




Draw ray lines to make sure you get the enlarged triangle in the correct position. The scale factor is 3 , so each of the sides of the enlarged triangle should be 3 times bigger than the sides of the original triangle
4. Enlarge this shape by scale factor \frac{1}{2} about the point O




The point O is the origin. Draw ray lines to make sure you get the enlarged triangle in the correct position. The scale factor is \frac{1}{2} so the triangle gets smaller.
5. Find the centre of enlargement




Draw ray lines through pairs of corresponding points. Draw all 3 of them to make sure you get the correct point
6. Find the centre of enlargement




Draw ray lines through pairs of corresponding points. Draw all 3 of them to make sure you get the correct point
Centre of enlargement GCSE questions
1. On the grid, enlarge the shape with scale factor 3, centre O.
(3 marks)
For one correct vertex
(1)
For second correct vertex
(1)
For fully correct triangle
(1)
2. Enlarge the shape with scale factor \frac{1}{2} centre (1,1).
(3 marks)
For one correct vertex
(1)
For second correct vertex
(1)
For fully correct triangle
(1)
3. Describe fully the single transformation that maps shape A onto shape B.
(3 marks)
Enlargement
For stating that it is an enlargement
(1)
Scale factor 2
For the correct scale factor
(1)
About (0,0)
For the correct coordinates of the centre of enlargement
(1)
Learning checklist
You have now learned how to:
- Use a centre of enlargement to enlarge a shape on a grid
- Use a centre of enlargement to enlarge a shape with a fractional scale factor
- Find a centre of enlargement
- Use a centre of enlargement to enlarge a shape with a negative scale factor (higher)
The next lessons are
Still stuck?
Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.