Graph transformations

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

Coordinates maths Translation Reflection Function notation (basic) Composite functions Types of graphs Sin graph Cos graph Tan graph

This topic is relevant for:

GCSE Maths Algebra Interpreting Graphs

Graph Transformations

Here we will learn about graph transformations, including translating vertically, translating horizontally and reflecting in the coordinate axes.

There are also graph transformation worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What are graph transformations?

Graph transformations involve performing transformations such as translations and reflections on the graph of a function.

In GCSE mathematics you may be asked to sketch a graph after a given transformation, or asked to write down the position of a coordinate after a transformation has been applied.

To do this we need to understand what each of the graph transformations look like and how they relate to the original function.

What are graph transformations?

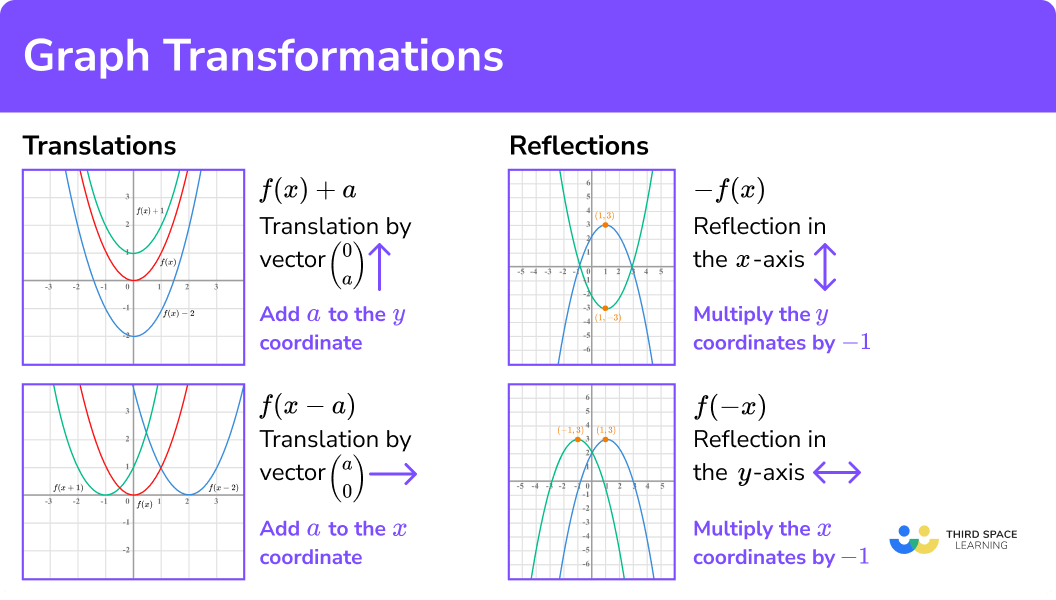
Transformations of functions

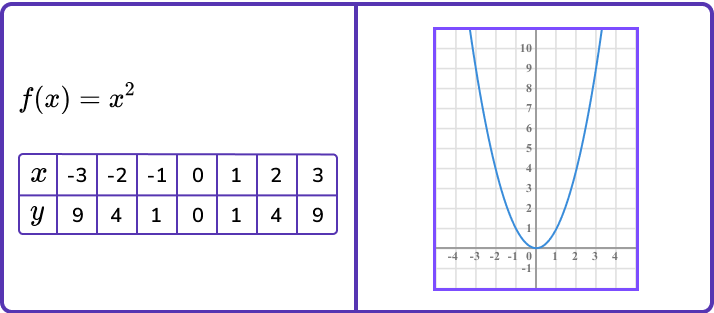
Let’s use a simple function such as $y=x^2$ to illustrate translations.

First you can write it using function notation and draw the graph using a table of values to help.

Translating the graph in a vertical direction.

This can be done by adding or subtracting a constant from the $y$ -coordinate. The transformed graph is green.

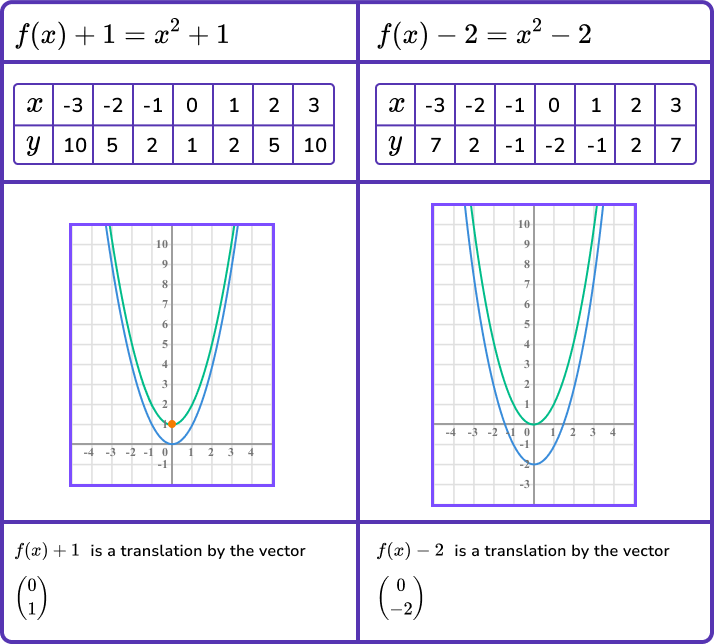
So translating vertically by the vector $\left( \begin{matrix} 0 \\ a \\ \end{matrix} \right)$ can be done using the transformation $f(x)+a.$

Translating the graph in a horizontal direction.

This can be done by adding or subtracting a constant from the $x$ -coordinate.

The transformed graph is blue.

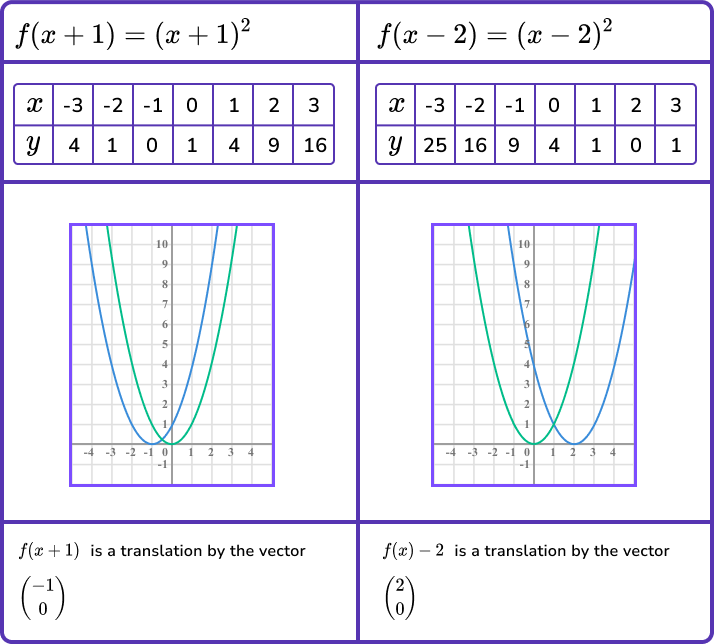
So translating vertically by the vector $\left( \begin{matrix} a \\ 0 \\ \end{matrix} \right)$ can be done using the transformation $f(x-a).$

Notice how the transformation $f(x+1)$ translated the graph to the left and not the right.

Reflecting a graph of a function.

The function $y=f(x)$ has a point $(1,3)$ as shown.

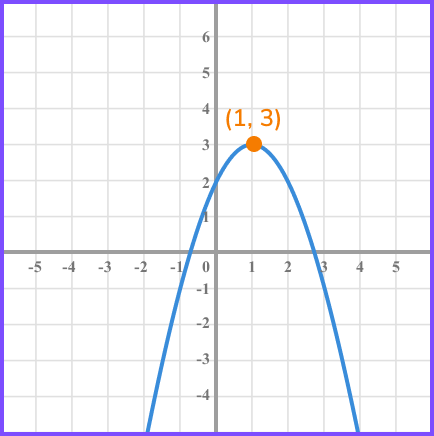
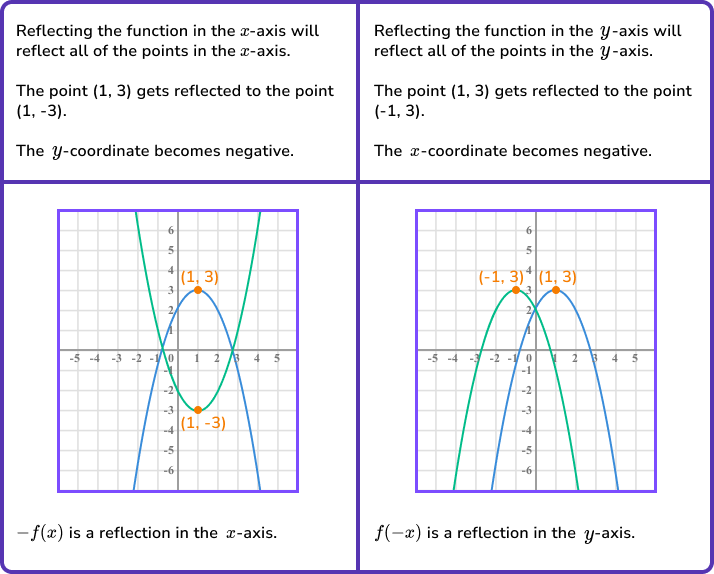
You will need to be able to apply all of these transformations to coordinates marked on unknown functions as well as sketch transformations of known functions such as the graphs of sin $(x),$ cos $(x)$ and tan $(x).$

Combinations of transformations

The different translations and reflections can be combined.

For example,

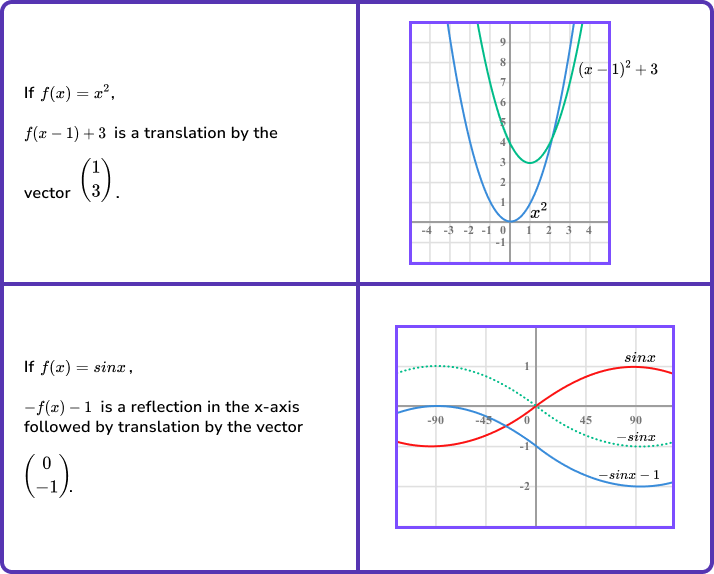
Further study

In A Level Mathematics these transformations of functions are looked at in more depth to include a horizontal stretch $f(ax)$ and a vertical stretch $af(x).$ These, and more complicated transformations, are applied to functions such as polynomials, exponentials, inverse functions and more complicated trigonometric functions.

In A Level Further Mathematics other transformations such as rotations, enlargements and shears are applied using matrices.

How to use graph transformations

In order to use graph transformations:

Determine whether the transformation is a translation or reflection.
Choose the correct transformation to apply from the rules.
$\quad \;\; f(x)+a$ is a translation in the $\bf{y-}$ direction.
$\quad \;\; f(x-a)$ is a translation in the $\bf{x-}$ direction.
$\quad \;\; -f(x)$ is a reflection in the $\bf{x-}$ axis.
$\quad \;\; f(-x)$ is a reflection in the $\bf{y-}$ axis.
Write down the required coordinate or sketch the graph.

Explain how to use graph transformations

Graph transformations worksheet

Get your free graph transformations worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Graph transformations worksheet

Get your free graph transformations worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Related lessons on interpreting graphs

Graph transformations is part of our series of lessons to support revision on interpreting graphs. You may find it helpful to start with the main interpreting graphs lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

Graph transformations examples

Example 1: applying a translation in the y-direction

The diagram shows the graph of $y=f(x)$ and a point on the graph $P(2,5).$

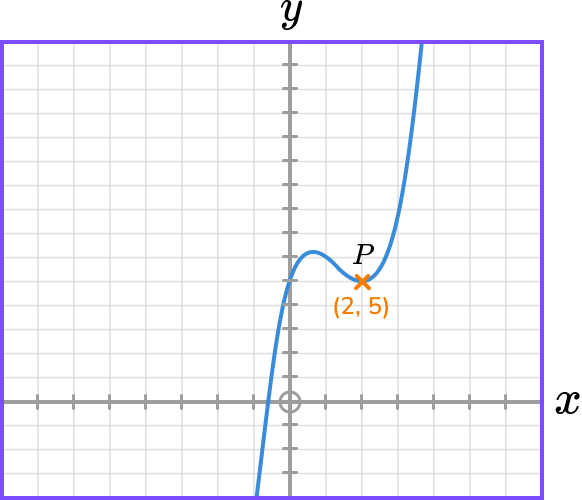
State the coordinate of the image of point $P$ on the graph $y=f(x)-4.$

Determine whether the transformation is a translation or reflection.

The function has been translated.

2Choose the correct transformation to apply from the rules.
$\quad \;\; f(x)+a$ is a translation in the $\bf{y-}$ direction.
$\quad \;\; \color{#C5C5C5} f(x-a)$ is a translation in the $\color{#C5C5C5} \bf{x-}$ direction.
$\quad \;\; \color{#C5C5C5} -f(x)$ is a reflection in the $\color{#C5C5C5} \bf{x-}$ axis.
$\quad \;\; \color{#C5C5C5} f(-x)$ is a reflection in the $\color{#C5C5C5} \bf{y-}$ axis.

$f(x)-4$ is a translation by the vector $\left( \begin{matrix} 0 \\ -4 \\ \end{matrix} \right).$ We need to subtract $4$ from the $y-$ coordinate.

3Write down the required coordinate or sketch the graph.

5-4 = 1

Therefore, the image of coordinate $P$ will be $(2,1).$

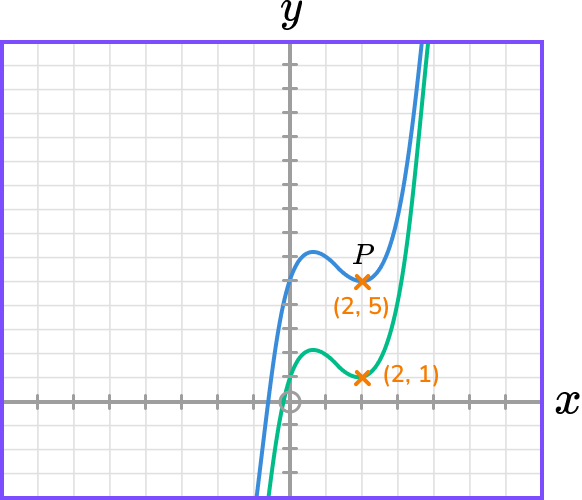
Example 2: applying a translation in the x-direction

The diagram shows the graph of $y=f(x)$ and a point on the graph $P(2,5).$

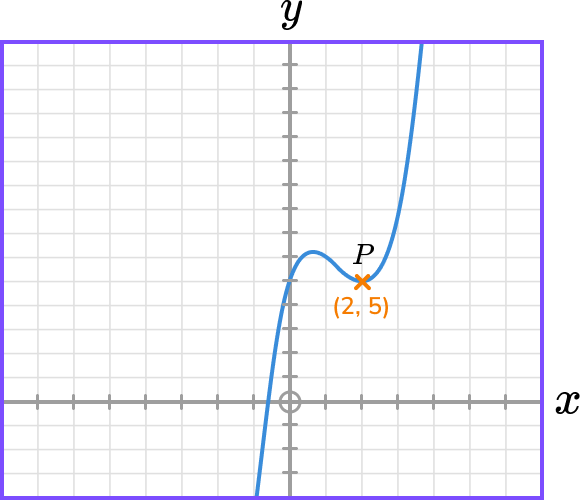
State the coordinate of the image of point $P$ on the graph $y=f(x+5).$

Determine whether the transformation is a translation or reflection.

The function has been translated.

Choose the correct transformation to apply from the rules.

$\color{#C5C5C5} f(x)+a$ is a translation in the $\color{#C5C5C5} \bf{y-}$ direction.
$f(x-a)$ is a translation in the $\bf{x-}$ direction.
$\color{#C5C5C5} -f(x)$ is a reflection in the $\color{#C5C5C5} \bf{x-}$ axis.
$\color{#C5C5C5} f(-x)$ is a reflection in the $\color{#C5C5C5} \bf{y-}$ axis.

$f(x+5)$ is a translation by the vector $\left( \begin{matrix} -5 \\ 0 \\ \end{matrix} \right).$ We need to subtract $5$ from the $x$ -coordinate.

Write down the required coordinate or sketch the graph.

2-5 =-3

Therefore, the image of coordinate $P$ will be $(-3,5).$

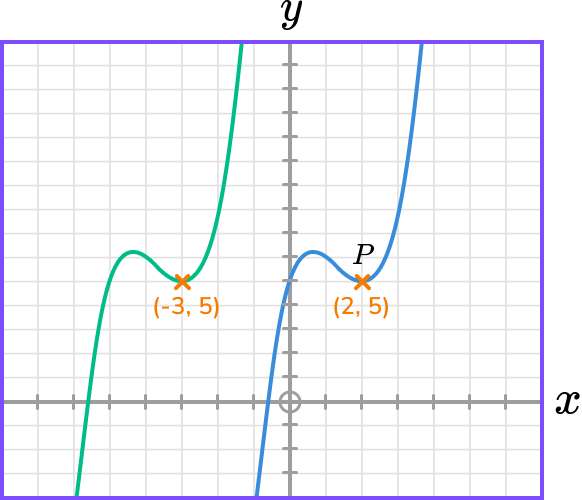
Example 3: applying a reflection in the x-axis

The diagram shows the graph of $y=f(x)$ and a point on the graph $P(2,5).$

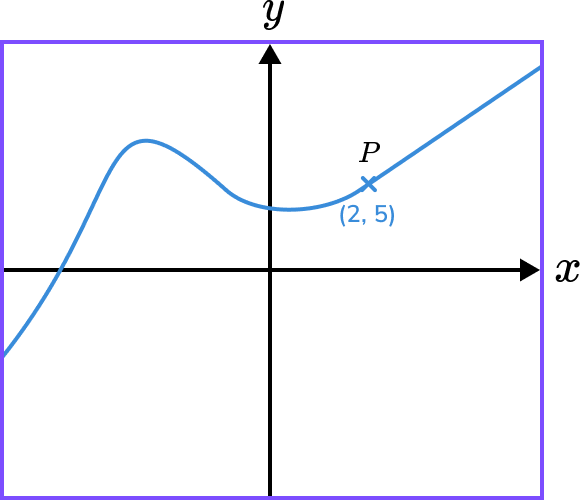
Sketch the graph and state the coordinate of the image of point $P$ on the graph $y=-f(x).$

Determine whether the transformation is a translation or reflection.

The function has been reflected.

Choose the correct transformation to apply from the rules.

$\color{#C5C5C5} f(x)+a$ is a translation in the $\color{#C5C5C5} \bf{y-}$ direction.
$\color{#C5C5C5} f(x-a)$ is a translation in the $\color{#C5C5C5} \bf{x-}$ direction.
$-f(x)$ is a reflection in the $\bf{x-}$ axis.
$\color{#C5C5C5} f(-x)$ is a reflection in the $\color{#C5C5C5} \bf{y-}$ axis.

We need to multiply the $y-$ coordinates by $-1.$

Write down the required coordinate or sketch the graph.

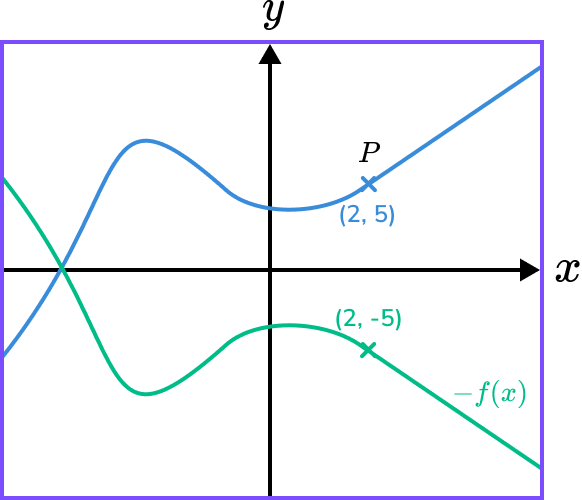
The image of the coordinate of $P$ will be $(2,-5).$

Example 4: applying a reflection in the y-axis

The diagram shows the graph of $y=f(x)$ and a point on the graph $P(2,5).$

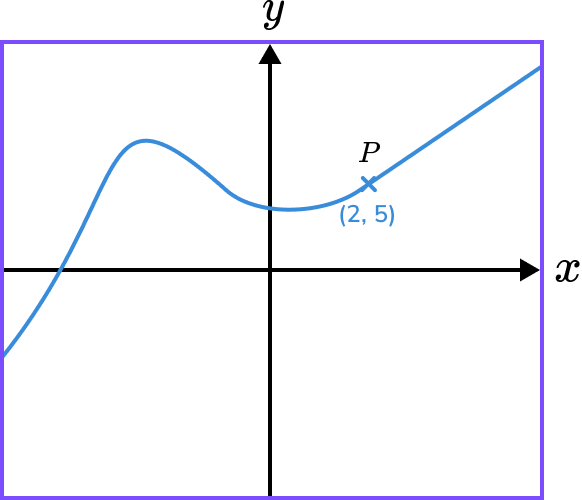
Sketch the graph and state the coordinate of the image of point $P$ on the graph $y=f(-x).$

Determine whether the transformation is a translation or reflection.

The function has been reflected.

Choose the correct transformation to apply from the rules.

$\color{#C5C5C5} f(x)+a$ is a translation in the $\color{#C5C5C5} \bf{y-}$ direction.
$\color{#C5C5C5} f(x-a)$ is a translation in the $\color{#C5C5C5} \bf{x-}$ direction.
$\color{#C5C5C5} -f(x)$ is a reflection in the $\color{#C5C5C5} \bf{x-}$ axis.
$f(-x)$ is a reflection in the $\bf{y-}$ axis.

We need to multiply the $x-$ coordinates by $-1.$

Write down the required coordinate or sketch the graph.

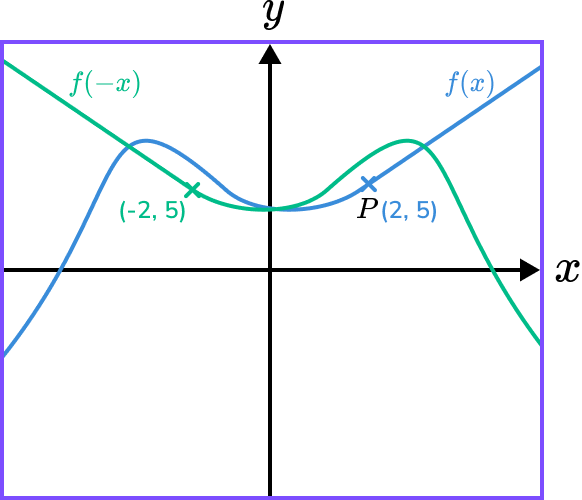
The image of coordinate $P$ will be $(-2,5).$

Example 5: applying a combination of translations

The image shows the graph of the quadratic function $f(x)$ which has a turning point at $(-3,-2).$

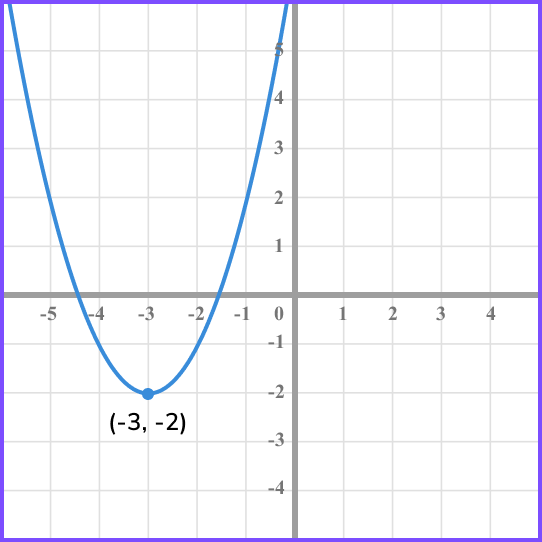
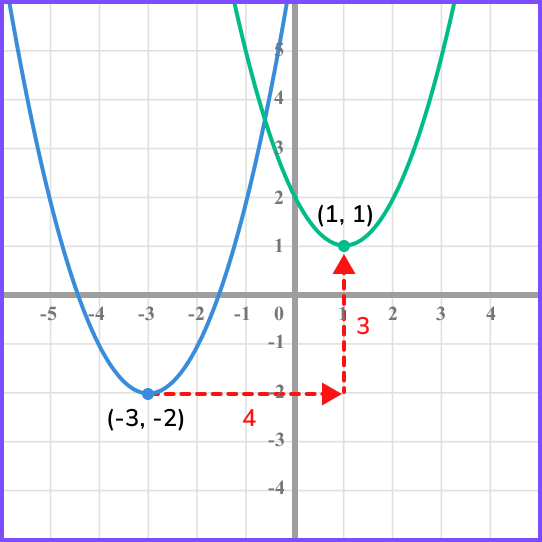
Sketch the graph of the function $f(x-4)+3,$ labelling the coordinate of the turning point.

Determine whether the transformation is a translation or reflection.

The function has been translated twice.

Choose the correct transformation to apply from the rules.

$f(x)+a$ is a translation in the $\bf{y-}$ direction.
$f(x-a)$ is a translation in the $\bf{x-}$ direction.
$\color{#C5C5C5} -f(x)$ is a reflection in the $\color{#C5C5C5} \bf{x-}$ axis.
$\color{#C5C5C5} f(-x)$ is a reflection in the $\color{#C5C5C5} \bf{y-}$ axis.

$f(x-4)+3$ is a translation by the vector $\left( \begin{matrix} 4 \\ 3 \\ \end{matrix} \right).$ We need to add $4$ to the $x-$ coordinate and add $3$ to the $y-$ coordinate.

Write down the required coordinate or sketch the graph.

\begin{aligned} &-3 + 4 = 1 \\\\ &-2 + 3 = 1 \end{aligned}

Therefore, the turning point will be $(1,1).$

Example 6: applying a combination of reflections and translations

The image shows the graph of the quadratic function $f(x)$ which has a turning point at $(-3,-2).$

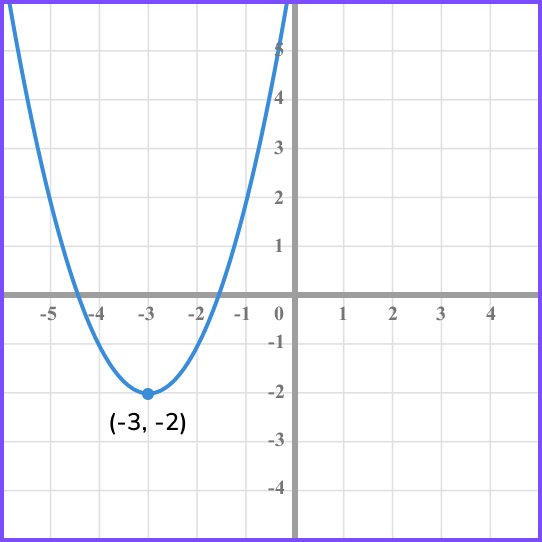
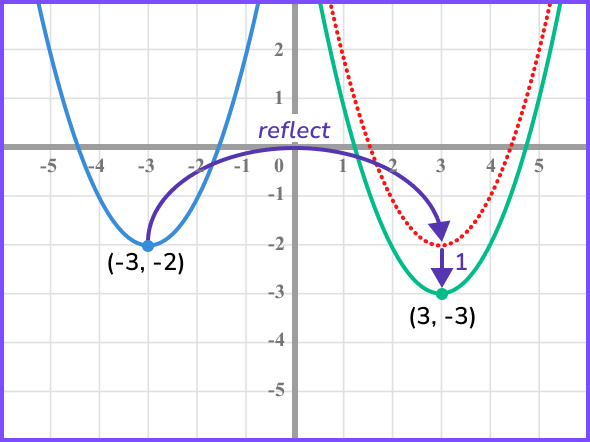
Sketch the graph of the function $f(-x)-1,$ labelling the coordinate of the turning point.

Determine whether the transformation is a translation or reflection.

The function has been reflected and translated.

Choose the correct transformation to apply from the rules.

$f(x)+a$ is a translation in the $\bf{y-}$ direction.
$\color{#C5C5C5} f(x-a)$ is a translation in the $\color{#C5C5C5} \bf{x-}$ direction.
$\color{#C5C5C5} -f(x)$ is a reflection in the $\color{#C5C5C5} \bf{x-}$ axis.
$f(-x)$ is a reflection in the $\bf{y-}$ axis.

$f(-x)-1$ is a reflection in the $y-$ axis followed by a translation by the vector $\left( \begin{matrix} 0 \\ -1 \\ \end{matrix} \right).$

We need to multiply the $x-$ coordinate by $-1$ and then subtract $1$ from the $y-$ coordinate.

Write down the required coordinate or sketch the graph.

\begin{aligned} &-3 \times -1 = 3 \\\\ &-2 - 1 = -3 \end{aligned}

Therefore, the turning point will be $(3,-3).$

Example 7: identifying a transformation

The curve with equation $y=f(x)$ is translated so that the minimum point at $(-1, 0)$ is translated to $(5,0).$ Find the equation of the new curve.

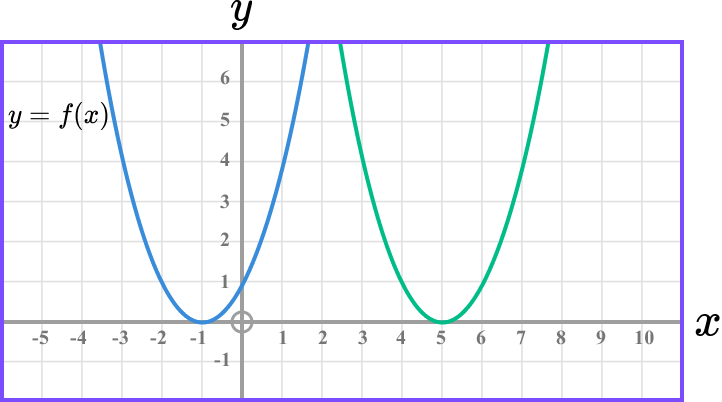
Determine whether the transformation is a translation or reflection.

The function has been translated.

Choose the correct transformation to apply from the rules.

Write down the required coordinate or sketch the graph.

In this case we need to write the equation of the new graph.

The graph has been translated by the vector $\left( \begin{matrix} 6 \\ 0 \\ \end{matrix} \right).$

The equation of the new graph is $y=f(x-6).$

Common misconceptions

Performing the wrong horizontal translation

A common mistake is thinking the transformation of $f(x+2)$ will mean the function translates to the right by $2.$ We can see that if we apply the transformation to the function, find a table of values and then plot the points, the function actually translates to the left.

This is because, when we use the transformation $f(x+2),$ the $y$ -values we obtain are for values of $x$ that would normally be two places to the right, so we are shifting those points to the left. $f(x+2)$ moves the graph to the left by $2, \ f(x-2)$ moves the graph to the right by $2.$

Reflecting in the wrong axes

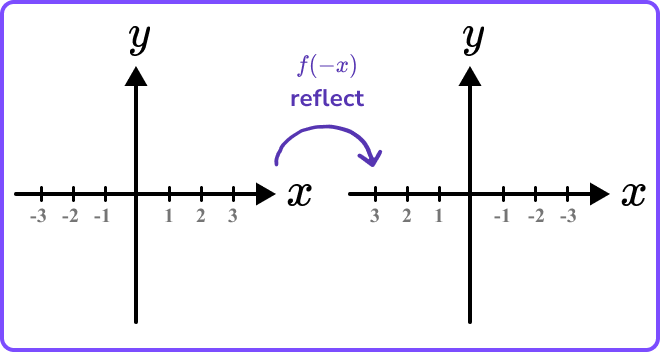
A common mistake is to confuse the reflections of $-f(x)$ and $f(-x).$

If $y=f(x), \ -f(x)=-y.$ This means the $y$ -values are being multiplied by $-1.$

Applying $f(-x)$ is changing the sign of the $x$ -value before applying the function.

It’s the same as taking the coordinate axes and switching the signs on the numbers on the $x-$ axis.

Practice graph transformations questions

(7,1)

(-1,1)

(3,-3)

(3,5)

$f(x-4)$ is a translation by $\left( \begin{matrix} 4 \\ 0 \\ \end{matrix} \right).$ Add $4$ to the $x-$ coordinate.

(-2,1)

(-2,5)

(0,3)

(-4,3)

$f(x)+2$ is a translation by $\left( \begin{matrix} 0 \\ 2 \\ \end{matrix} \right).$ Add $2$ to the $y-$ coordinate.

(5,1)

(-1,5)

(1,-5)

(-5,-1)

$f(-x)$ is a reflection in the $y-$ axis. Multiply the $x-$ coordinate by $-1.$

(4,2)

(-4,2)

(4,-2)

(-2,-4)

$-f(x)$ is a reflection in the $x-$ axis. Multiply the $y-$ coordinate by $-1.$

(5,-4)

(5,6)

(-1,6)

(-1,-4)

$f(x+3)+5$ is a translation by $\left( \begin{matrix} -3 \\ 5 \\ \end{matrix} \right).$ Subtract $3$ from the $x-$ coordinate and add $5$ to the $y-$ coordinate.

(-5,-5)

(-5,1)

(5,-1)

(5,5)

$-f(x)-3$ is a reflection in the $x-$ axis followed by a translation by $\left( \begin{matrix} 0 \\ -3 \\ \end{matrix} \right).$ Multiply the $y-$ coordinate by $-1,$ then subtract $3.$

Graph transformation GCSE questions

1. The diagram shows the function $f(x)$ and the point $P(-1,2).$

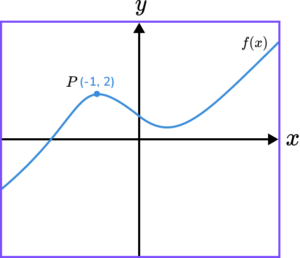
Graph transformations gcse question 1

Write down the coordinates of the image of $P$ after the following transformations.

(a) $f(x-2)$

(b) $f(x)-2$

(d) $-f(x+3)$

(5 marks)

Show answer

(a) $(1,2)$

(1)

(b) $(-1,0)$

(1)

(d)

Correct $x$ -value of $-4$

(1)

Correct $y$ -value of $-2$

(1)

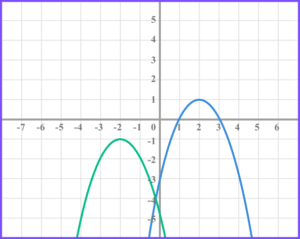
2. The diagram shows the graph of the function $f(x).$

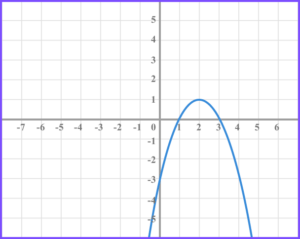
Graph transformations gcse question 2 image 1

(a) On the grid below draw the function $f(x+5)$ .

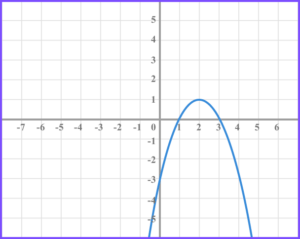
Graph transformations gcse question 2 image 2

(b) On the grid below draw the function $f(-x)-2$ .

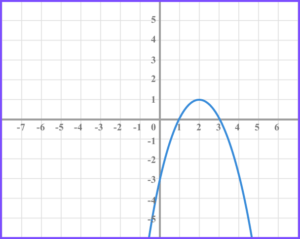
Graph transformations gcse question 2 image 4

(3 marks)

Show answer

(a)

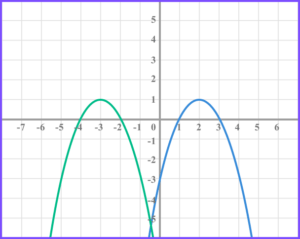
Graph transformations gcse question 2 image 3

(1)

(b)

Reflection shown with correct $x$ -value of turning point.

(1)

Reflection shown with correct $y$ -value of turning point.

(1)

Graph transformations gcse question 2 image 5

3. The graphs of $f(x) = sin \ x$ and $g(x) =cos \ x$ are shown below.

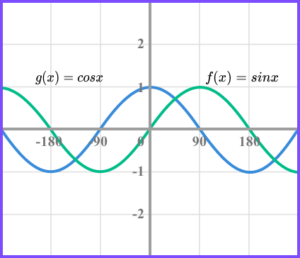
Graph transformations gcse question 3 image 1

Complete the following table, giving each transformation of $g(x)$ in terms of a transformation of $f(x).$ The first one has been done for you.

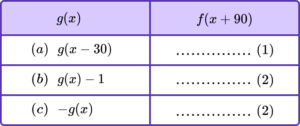
Graph transformations gcse question 3 image 2

(5 marks)

Show answer

(a) $f(x+60)$

(1)

(b)

$+90$ in brackets

(1)

$-1$ outside brackets

(1)

f(x+90)-1

(c)

$-90$ in brackets, $f(x-90)$

(2)

$-1$ in front of $f$

(1)

$+90$ in brackets

(1)

-f(x+90)

Learning checklist

You have now learned how to:

Sketch translations and reflections of the graph of a given function

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.