Reflection

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

Learn more

In order to access this I need to be confident with:

Symmetry Lines of symmetry 2D shapes Coordinates maths Straight line graphs

This topic is relevant for:

GCSE Maths Geometry and Measure

Reflection

Here we will learn how to reflect 2D shapes on grid paper and how to describe reflections.

There are also reflection worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is reflection?

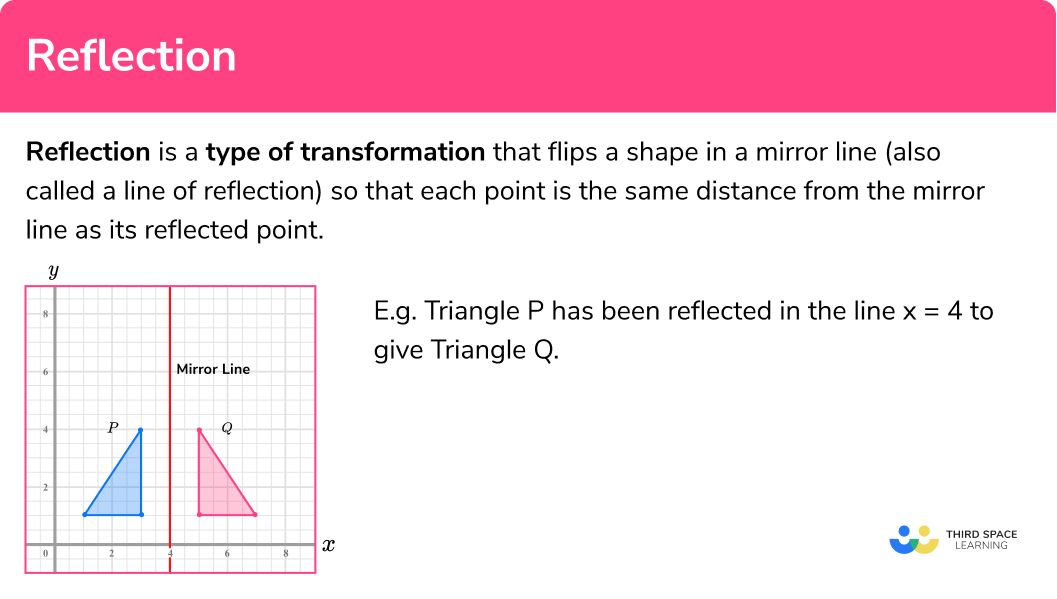
Reflection is a type of transformation that flips a shape in a mirror line (also called a line of reflection) so that each point is the same distance from the mirror line as its reflected point.

E.g.

Triangle $P$ has been reflected in the line $x=4$ to give Triangle $Q$ .

Triangle $P$ is the object and Triangle $Q$ is the image.

When an object is reflected the object and the image are mirror images of each other.

We can see that each point of triangle $P$ is the same distance from the mirror line as the corresponding point on triangle $Q$ .

The two triangles are congruent because they are the same shape and the same size.

See also: Transformations

What is reflection?

How to use reflections

In order to reflect a shape on a grid:

Reflect the first point.
Reflect the other points.
Finish the diagram.

How to use reflections

Reflection maths worksheet

Get your free reflection maths worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Reflection maths worksheet

Get your free reflection maths worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Reflection maths examples

Example 1: reflect a shape on a grid

Reflect the shape in the line:

Reflect the first point.

Choose the first point to reflect. It is easier to start with a point which is closest to the mirror line (the line of reflection). The new point will be exactly the same distance away from the mirror line as the original point.

2Reflect the other points.

Here is a second point being reflected to give its image. The remaining two points have also been added.

3Finish the diagram.

To finish the diagram we can join up the reflected points.

Example 2: reflect a shape on a grid

Reflect the shape in the line:

Reflect the first point.

2Reflect the other points.

Here is a second and a third point being reflected to give its image. The remaining point is on the mirror line and does not move (it is an invariant point).

3Finish the diagram.

To finish the diagram we can join up the reflected points.

See also: Symmetry

How use reflections on a coordinate grid

In order to reflect a shape on a coordinate grid:

Draw the mirror line.
Reflect the first point.
Reflect the other points.
Finish the diagram.

Reflections on a coordinate grid examples

Example 3: reflect a shape on a coordinate grid

Reflect Triangle $P$ in the line $x = 4$ :

Draw the mirror line.

The mirror line is $x = 4$ (the line of reflection). This is a vertical line. Draw this on the diagram.

2Reflect the other points.

Choose the first point to reflect. It is easier to start with a point which is closest to the mirror line (the line of reflection). Let’s reflect the point $(3,1)$ . The new point will be exactly the same distance away from the mirror line as the original point.

3Reflect the other points.

Here is a second point $(1,4)$ being reflected to give its image.

We can reflect the third point $(1,1)$ .

4Finish the diagram.

To finish the diagram we can join up the reflected points.

Here Triangle $Q$ is the image of Triangle $P$ .

Example 4: reflect a shape

Reflect Triangle $P$ in the line $y = 3$ :

Draw the mirror line.

The mirror line is $y = 3$ (the line of reflection). This is a horizontal line. Draw this on the diagram.

2Reflect the other points.

Choose the first point to reflect. It is easier to start with a point which is closest to the mirror line (the line of reflection). Let’s reflect the point $(3,2)$ . The new point will be exactly the same distance away from the mirror line as the original point.

3Reflect the other points.

Here is a second point $(1,4)$ being reflected to give its image.

We can reflect the third point $(4,0)$ .

4Finish the diagram.

To finish the diagram we can join up the reflected points.

Here Triangle $Q$ is the image of Triangle $P$ .

How to describe reflections

In order to describe a reflection of a shape on a coordinate grid:

Pair up the points.
Identify the midpoints.
Join the midpoints.
State the equation of the line.

Describing reflections examples

Example 5: describe a reflection

Describe the transformation of Shape $A$ to Shape $B$

Pair up the points.

Try to match up the corresponding point on the two shapes and draw a connecting line. Try to do this with more than one set of points.

2Identify the midpoints.

Identify the midpoints of these connecting lines. This will help us to draw in the line of reflection.

3Join the midpoints.

Draw a straight line through the midpoints.

4State the equation of the line.

The equation of the line is $y = 4$ .

The transformation is a reflection in the line $y = 4$

Example 6: describe a reflection

Describe the transformation of Shape $A$ to Shape $B$

Pair up the points.

Try to match up the corresponding point on the two shapes and draw a connecting line. Try to do this with more than one set of points.

2Identify the midpoints.

Identify the midpoints of these connecting lines. This will help us to draw in the line of reflection.

3Join the midpoints.

Draw a straight line through the midpoints.

4State the equation of the line.

The equation of the line is $y = x$ .

The transformation is a reflection in the line $y = x$

Common misconceptions

Overlapping shapes

The original shape (the object) and its reflection (the image) are allowed to overlap each other.

E.g.

Diagonal mirror line (the line of reflection)

Diagonal mirror lines can be tricky. It is worth turning the diagram so that the mirror line is either horizontal or vertical to make the reflections easier to carry out.

Describe transformations fully

When you are asked to describe a transformation make sure you state which kind of transformation it is and any other details. So for reflections we need to state that it is a reflection and give the equation of the line of reflection.

Practice reflection maths questions

The corresponding points on the object and the image must be equidistant (the same distance) from the mirror line.

The corresponding points on the object and the image must be equidistant (the same distance) from the mirror line. The object and the image should be congruent – the same shape and the same size.

The line $y = 4$ is a horizontal line going through $4$ on the $y$ -axis. The corresponding points on the object and the image must be equidistant (the same distance) from the mirror line.

The $y$ -axis is the vertical axis. The corresponding points on the object and the image must be equidistant (the same distance) from the mirror line. The object and the image should be congruent – the same shape and the same size.

reflection in $x=6$

reflection in $x=5$

reflection in $y=5$

transformation in $x=5$

You must state that the transformation is a reflection. The line of reflection is a vertical line, so the equation is $x=a$ , where $a$ is a number. The corresponding points on the object and the image must be equidistant (the same distance) from the mirror line.

reflection in $x$ -axis

reflection in $y$ -axis

reflection in $y=-x$

reflection in $y=x$

The line of reflection is a diagonal line. The corresponding points on the object and the image must be equidistant (the same distance) from the mirror line. The mirror line goes through the points $(1,-1), (2,-2), (3,-3)$ and so on.

Reflection maths GCSE questions

1. Reflect the shaded shape in the mirror line.

(2 marks)

Show answer

for at least $2$ correct vertices

(1)

for correct reflection in the correct position

(1)

2. On the grid below, reflect the shape in the line with the equation $x=1$

(2 marks)

Show answer

for drawing the correct mirror line

(1)

for correct reflection in the correct position

(1)

3. Describe fully the single transformation that maps shape $A$ onto shape $B$ .

(2 marks)

Show answer

Reflection in $x$ -axis (or $y=0$ )

stating reflection

(1)

for giving the correct line of reflection

(1)

Learning checklist

You have now learned how to:

Reflect 2D shapes including polygons on grid

Reflect 2D shapes including polygons on coordinate grid with x-axis and y-axis

Identify properties of, and describe the results of reflections applied to given figures

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.