GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

Teacher-trusted tutoring

In order to access this I need to be confident with:

Parts of a circle Angles in polygons Angles on a straight line Angles around a point Angles in parallel lines Triangles

This topic is relevant for:

GCSE Maths Geometry and Measure Circle Theorems

Angles In The Same Segment

Angles In The Same Segment Are Equal

Here we will learn about the circle theorem: angles in the same segment, including its application, proof, and using it to solve more difficult problems.

There are also circle theorem worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is angles in the same segment are equal?

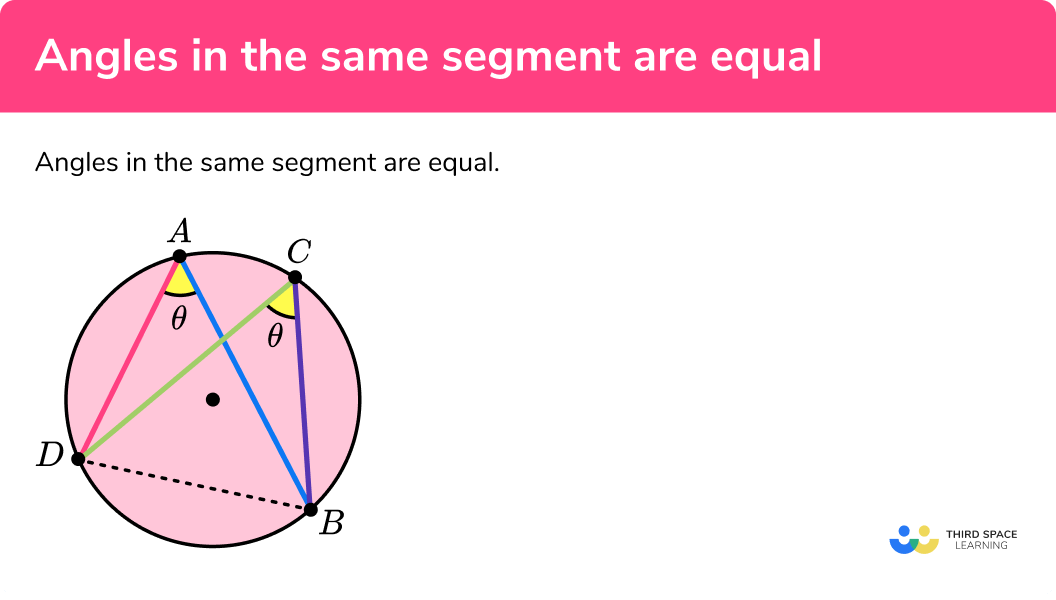
Angles in the same segment are equal

In the diagram above, $BD$ is a chord that divides the circle into the major and minor segments. The two points $A$ and $C$ on the circumference are joined to two other points on the circumference $B$ and $D$ . The angle $DAB$ is the same as angle $DCB$ . This is the same for any point that is placed on the major arc and so angles in the same segment are equal.

If the point is placed on the minor arc in the other segment, it would be a different angle, but all angles on the minor arc would be the same. Here, $x=180-θ$ for any value of θ.

What is angles in the same segment are equal?

Key parts of a circle needed for this theorem

Below is a diagram showing the key parts of a circle for this theorem:

A chord is a straight line that meets the circumference in two places. The longest chord in a circle is the diameter.
The major segment is the larger segment of a circle when it is enclosed by a chord and the major arc.
The minor segment is the smaller part of a circle when it is cut by a chord and the minor arc.
An arc is a part of the circumference. The major arc is longer than the minor arc.

Subtended angles

An angle within a circle is created by two chords meeting at a point on the circumference of a circle. The diagrams below show the angle subtended by arc $AC$ from point $B$ for two different circles.

Proving that angles in the same segment are equal

To be able to prove the theorem, you need to know the following circle theorems:

The angle at the centre is twice the angle at the circumference

We start by labelling the two angles at the circumference $a$ and $b$

2Plot the centre of a circle and draw two radii from the centre to the circumference (here these are dashed lines). Label the angle between the two radii $c$ .

3Let us inspect the angles $a$ and $c$ .

4We know that the angle at the centre is twice the angle at the circumference. This means that if the angle at the centre is equal to $2x$ , the angle at the circumference (which was our angle $a$ )is now equal to half of $2x$ , or just $x$ .

5Let us now inspect angles $b$ and $c$ .

6Again, we know that the angle at the centre is twice the angle at the circumference and so if we say that the angle $c$ is equal to $2x$ , the angle $b$ is equal to $x$ .

7We now have the current situation where $a$ and $b$ are equal to $x$ and the angle $c$ is equal to $2x$ .

8This means that the two angles at the circumference are the same size and therefore we can state angles in the same segment are equal.

How to use the angle in the same segment theorem

In order to use the fact that angles in the same segment are equal:

Locate the key parts of the circle for the theorem
Use other angle facts to determine an angle at the circumference in the same segment
Use the angle in the same segment theorem to state the other missing angle

How to use the angle in the same segment theorem

Circle theorems worksheet (includes angles in the same segment)

Get your free angles in the same segment worksheet of 20+ circle theorems questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Circle theorems worksheet (includes angles in the same segment)

Get your free angles in the same segment worksheet of 20+ circle theorems questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Tangent of a circle is one of 7 circle theorems you will need to know. You may find it helpful to start with our main circle theorems page and then look in detail at the rest.

Angles in the same segment examples

Example 1: standard diagram

Below is a circle with centre $O$ . $AC$ and $BD$ are chords. Calculate the size of angle $CAD$ .

Locate the key parts of the circle for the theorem.

Here we have:

The angle $CBD = 47°$
$AC$ and $BD$ are chords
The angle $CAD = θ$

2Use other angle facts to determine an angle at the circumference in the same segment.

We already know that $DBC = 47°$ so we do not need to use any other angle fact to determine this angle for this example.

3Use the angle in the same segment theorem to state the other missing angle.

The angle $CAD$ is in the same segment as the angle $CBD$ and so we can state the angle of $CAD$

$CAD = CBD = 47°$

Example 2: angles on a straight line

$A, B, C,$ and $D$ are points on a circle with centre $O$ . Calculate the size of the angle $CBD$ .

Locate the key parts of the circle for the theorem.

Here we have:

The angle $BDA = 65°$
$AC, AD, BC,$ and $BD$ are chords
The angle $CED = 88°$
The angle $CBD = θ$

Use other angle facts to determine an angle at the circumference in the same segment.

Angles on a straight line total $180°$ so angle $BEC = 180-88 = 92°$ .

Use the angle in the same segment theorem to state the other missing angle.

The angle $BCA$ is in the same segment as the angle $BDA$ and so they are equal angles. This means angle $BCA = 65°$ .

As angles in a triangle total $180°$ , angle $CBD$ can now be calculated:

$CBD = 180 - (92+65)$

$CBD = 23°$

Example 3: angles in a triangle

The circle with centre $O$ has four points on the circumference. The two chords $AC$ and $BD$ intersect at the point $E$ . Calculate the size of angle $ABE$ .

Locate the key parts of the circle for the theorem.

Here we have:

The angle $CDB = 44°$
$BD$ is a diameter
$AB, AC,$ and $CD$ are chords
The angle $CED = 79°$
The angle $ABE = θ$

Use other angle facts to determine an angle at the circumference in the same segment.

Vertically opposite angles are equal and so the angle $BEA = 70°$ .

Use the angle in the same segment theorem to state the other missing angle.

Angle $CDB$ is in the same segment as the angle $CAB$ and so they are equal. This means we can calculate the size of angle $ABE$ as angles in a triangle total $180°$ :

$ABE = 180 - (79+44)$

$ABE = 57°$

Example 4: angle at the centre

$A, B, C,$ and $D$ are points on the circumference of the circle with centre $O$ . $BOD$ is a straight line. Calculate the size of angle $ABD$ .

Locate the key parts of the circle for the theorem.

Here we have:

The angle $AOD = 74°$
$OA = OD$ = Radii
$BD$ is a diameter
$AB, AC$ and $CD$ are chords
The angle $ABD = θ$

Use other angle facts to determine an angle at the circumference in the same segment.

The angle at the centre is twice the angle at the circumference and so the angle ACD is equal to:

$ACD=74\div2$

$ACD=37°$

Use the angle in the same segment theorem to state the other missing angle.

Angle $ABD$ is in the same segment as angle $ACD$ and so $ABD = 37°$ .

Example 5: cyclic quadrilateral

$ABCD$ are vertices of a cyclic quadrilateral. The circle has centre $O$ . The chords $AC$ and $BD$ intersect at the point $E$ . Calculate the size of the angle $ABE$ .

Locate the key parts of the circle for the theorem.

Here we have:

The angle $ADC = 94°$
The angle $CAD = 21°$
The angle $BEC = 88°$
$A, B, C$ and $D$ are all connected by chords
The angle $ABD = θ$

Use other angle facts to determine an angle at the circumference in the same segment.

Here, angle properties are very important. Angles on a straight line total $180°$ , angle $CED = 180 - 88 = 92°$ . Vertically opposite angles are the same and so angle $AED = 88°$ . Angles in a triangle total $180°$ , and so angle $ADE = 180 - (88+21) = 71°$ . This means that angle $CDE = 94 - 71 = 23°$ . Placing all this information into the diagram, we have:

The angle $DCE$ can now be calculated as it is the third angle in the triangle. This means that:

$DCE = 180 - (92+23)$

$DCE = 65°$

Use the angle in the same segment theorem to state the other missing angle.

Angle $ACD$ is in the same segment as angle $ABD$ and so they are equal. This means that angle $ABD = 65°$ .

Example 6: complex diagram

$A, B, C, D,$ and $E$ are points on a circle with centre $O$ . The lines $AB$ and $CD$ are parallel. Calculate the value of angle $BDC$ .

Locate the key parts of the circle for the theorem.

Here we have:

The angle $AGE = 84°$
The angle $EBD = 8°$
$AC$ and $BD$ are diameters
$BE, CE$ and $CD$ are chords
The angle $BDC = θ$

Use other angle facts to determine an angle at the circumference in the same segment.

Vertically opposite angles are the same so angle $BGO = 84°$ . The missing angle in the triangle $AOB = 180-(84+8) = 88°$ . Angles on a straight line total $180°$ , so angle $BOC = 180 - 88 = 92°$ .

The angle at the centre is twice the angle at the circumference and so angle $BEC = 92\div 2 = 46°$

Use the angle in the same segment theorem to state the other missing angle.

As angle $BEC$ is in the same segment as the angle $BDC$ we can say that angle $BEC$ = angle $BDC$ or $BDC=46°$ .

Common misconceptions

Angle is double or half the original

The other angle in the same segment at the circumference is doubled or halved instead of it being the same.

Angles add up to 90° or 180°

The two angles that are in the same segment at the circumference total $90°$ (or $180°$ if one angle is obtuse).

Practice angles in the same segment questions

10^{\circ}

79^{\circ}

22^{\circ}

11^{\circ}

$CBD = CAD = 11^{\circ}$ (angles in the same segment are equal)

49^{\circ}

47^{\circ}

43^{\circ}

50^{\circ}

$BEC = 84^{\circ}$ (angles on a straight line)
$BCE = 47^{\circ}$ (angles in the same segment are equal)
$CBE = 180 – (84+47) = 49^{\circ}$ (angles in a triangle)

38^{\circ}

51^{\circ}

52^{\circ}

44.5^{\circ}

$CED = 89^{\circ}$ (angles on a straight line)
$DCE = 180 – (91+38) = 51^{\circ}$ (angles in a triangle)
$ABE = 51^{\circ}$ (angles in the same segment are equal)

54^{\circ}

27^{\circ}

108^{\circ}

44^{\circ}

$AOD = 360 – 306 = 54^{\circ}$ (angles at a point)
$ACD = 54 ÷ 2=27^{\circ}$ (angle at the centre is twice the angle at the circumference)
$ABD = ACD = 27^{\circ}$ (angles in the same segment are equal).

84^{\circ}

52^{\circ}

56^{\circ}

42^{\circ}

$BAD = 180 – 84 = 96^{\circ}$ (opposite angles in a cyclic quadrilateral total $180^{\circ}$ )
$BAE = 96 – 52 = 44^{\circ}$
$ABE = 180 – (80+44) = 56^{\circ}$ (angles in a triangle)

122^{\circ}

64^{\circ}

174^{\circ}

116^{\circ}

$BCD = 180 – 58 = 122^{\circ}$ (angles in opposing segments total $180^{\circ}$ in a cyclic quadrilateral).

Angles in the same segment GCSE questions

1. Use the information in the diagram below to calculate the size of angle $ACB$ . Explain your answer.

(4 marks)

Show answer

ADB = 180 - (78 + 65) = 37^\circ

(1)

Angles in a triangle total $180^\circ$

(1)

ACB = ADB = 37^\circ

(1)

Angles in the same segment are equal

(1)

2. $A, B, C, D$ are points on the circle with centre $O$ . The chords $AC$ and $BD$ intersect at the point $E$ . The tangent $FG$ goes through the point $B$ . Terry says that angle $ACD = 11^\circ$ . Is he correct?

Explain your answer.

(5 marks)

Show answer

ABE = 90 - 75 = 15^\circ

(1)

The tangent meets the radius at a right angle

(1)

θ = ACD = ABD = 15^\circ

(1)

Angles in the same segment are equal

(1)

No, Terry is wrong

(1)

3 (a). The circle with centre $O$ has $4$ points on the circumference, $A, B, C,$ and $D$ . Calculate the size of angle $ADB$ .

(b). Hence state the size of angle $AED$ in the diagram below.

(6 marks)

Show answer

(a) $BAC = 68\div 2 = 34^∘$

(1)

Angle at the centre is twice the angle at the circumference

(1)

180 - (34 + 42) = 104^\circ

(1)

Angles in a triangle total $180^\circ$

(1)

(b) $AED = 42^\circ$

(1)

Angles in the same segment are equal

(1)

Learning checklist

You have now learned how to:

Apply and prove the standard circle theorems concerning angles, radii, tangents and chords, and use them to prove related results

The next lessons are

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.